Tangente

Kreis mit Tangente, Sekante und Passante

Schwarzer Graph und rote Tangente

Eine Tangente (von lateinisch: tangere = „berühren“) ist in der Geometrie eine Gerade, die eine gegebene Kurve in einem bestimmten Punkt berührt. Ein Beispiel ist eine Schiene, die von einem Rad in einem einzigen Punkt berührt wird. Tangente und Kurve haben im Berührungspunkt die gleiche Richtung. Die Tangente ist in diesem Punkt die beste lineare Annäherung für die Kurve.

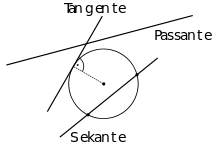
Besonders einfach sind die Verhältnisse beim Kreis: Alle Geraden können bezüglich eines Kreises unterschieden werden in Sekanten, Tangenten und Passanten – je nachdem, ob sie mit dem Kreis zwei Punkte, einen oder gar keinen Punkt gemeinsam haben. Die Kreistangente trifft den Kreis also in genau einem Punkt. Sie steht dort senkrecht auf dem zu diesem Punkt gehörenden Berührungsradius.

Auch im allgemeinen Fall steht die Tangente senkrecht auf dem zum Berührungspunkt gehörenden Radius des Krümmungskreises, sofern dieser existiert. Sie kann aber mit der Ausgangskurve noch weitere Punkte gemeinsam haben. Ist ein weiterer Punkt (der Ausgangskurve oder einer anderen Kurve) ebenfalls Berührpunkt, so spricht man von einer Bitangente.

Tangente in der Analysis

Ist die gegebene Kurve der Graph einer reellen Funktion f, dann ist die Tangente t im Punkt P(x₀ | f(x₀)) die Gerade, die dort die gleiche Steigung wie die Kurve hat. Die Steigung m_T der Tangente t ist also gleich der ersten Ableitung von f an der Stelle x₀: m_T = f'(x₀). Die Gleichung der Tangente t ist somit:

$y \, = \, f(x_0) + f'(x_0) \cdot (x-x_0)$

(siehe auch: Punkt-Steigungs-Formel).

Die Tangente entspricht der besten linearen Näherung für die Funktion f an der Stelle x₀:

$f(x) \, \approx \, f(x_0) + f'(x_0) \cdot (x-x_0)$ für $x \, \approx \, x_0$

Differenzialgeometrie

Eine Kurve im $\mathbb{R}^n$ sei durch eine auf dem reellen Intervall [a,b] definierte Funktion $\gamma:\,[a,b]\to\mathbb{R}^n$ gegeben. Ist $\gamma (t_0)\,$ (mit $t_0 \in [a,b]$) ein Kurvenpunkt, so nennt man die erste Ableitung von γ an der Stelle t₀ (also $\gamma\,'(t_0)\,$) einen Tangentialvektor. Eine Kurventangente in diesem Punkt ist eine Gerade durch den Punkt γ(t₀), die die gleiche Richtung wie der Tangentialvektor hat.

Voraussetzungen

Eine Tangente kann in der Regel nur existieren, wenn die zugrunde liegende Funktion (oder die zugrunde liegenden Funktionen) differenzierbar ist/sind.

Ein einfaches Gegenbeispiel:

Die Betragsfunktion $x \mapsto |x|$ ist an der Stelle x = 0 nicht differenzierbar. Der zugehörige Funktionsgraph hat an dieser Stelle einen „Knick“, so dass es hier sinnlos ist, von der Tangente zu sprechen.

An einer Knickstelle existiert aber möglicherweise eine rechtsseitige und/oder eine linksseitige Ableitung; es kann also eine Rechts-Tangente und/oder eine Links-Tangente geben.

Ist eine Funktion an einer Stelle x₀ ihres Definitionsbereichs zwar nicht differenzierbar, strebt der Wert der Ableitungsfunktion für $x \to x_0$ betragsmäßig jedoch gegen Unendlich, so hat der Funktionsgraph an dieser Stelle eine senkrechte Tangente (eine Parallele zur y-Achse als Tangente). Ein Beispiel hierfür ist die Funktion $x\mapsto \sqrt[3]{x}$, die für alle reellen Zahlen definiert ist, aber an der Stelle x₀ = 0 nicht differenzierbar ist. Dort liegt eine senkrechte Tangente vor.

Siehe auch

• Differentialrechnung
• Kurvendiskussion
• Tangentialraum
• Subtangente

Weblinks

 Wiktionary: Tangente – Bedeutungserklärungen, Wortherkunft, Synonyme, Übersetzungen