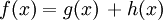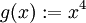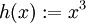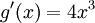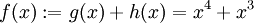Differenzregel

Die Summenregel ist in der Mathematik eine der Grundregeln der Differentialrechnung. Sie besagt, dass die Summe aus zwei differenzierbaren Funktionen wieder differenzierbar ist und dass eine solche Summe aus Funktionen gliedweise differenziert werden kann.

Regel

Die Funktionen g und h seien in einem gemeinsamen Intervall definiert, das die Stelle x₀ enthält. An dieser Stelle x₀ seien beide Funktionen differenzierbar. Dann ist auch die Funktion f mit

$f(x) = g(x)\, + h(x)$

an der Stelle x₀ differenzierbar, und es gilt

$f'(x_0) = g'(x_0) + h'(x_0)\,$.

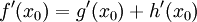Beispiel

Die Funktionen

$\ g(x) := x^4$

$\ h(x) := x^3$

sind auf $\mathbb{R}$ differenzierbar mit den Ableitungsfunktionen

$\ g'(x) = 4x^3$

$\ h'(x) = 3x^2$.

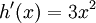Daher ist auch die Funktion

$\ f(x) := g(x) + h(x) = x^4 + x^3$

auf $\mathbb{R}$ differenzierbar mit der Ableitungsfunktion

$\ f'(x) = g'(x) + h'(x) = 4 x^3 + 3 x^2$.

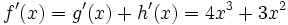Folgerungen

• Differenzregel: Betrachtet man die Differenz f = g − h = g + ( − h) für Funktionen g und h, die in x₀ differenzierbar sind, ergibt sich aus der Summenregel und der Faktorregel, dass f in x₀ differenzierbar ist und für die Ableitung f'(x) = g'(x) − h'(x) gilt.
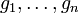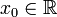• Zusammen mit der Faktorregel ergibt sich: Sind $g_1, \ldots, g_n$ in $x_0 \in \mathbb{R}$ differenzierbare Funktionen und 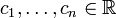$c_1, \ldots, c_n \in \mathbb{R}$ reelle Konstanten, dann ist die Linearkombination 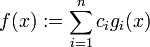$f(x) := \sum_{i=1}^nc_ig_i(x)$ wiederum in x₀ differenzierbar mit (gliedweise differenzierter) Ableitungsfunktion

  $f'(x_0) = \left(\sum_{i=1}^nc_ig_i\right)'(x_0) = \sum_{i=1}^nc_i {g_i}'(x_0)$.

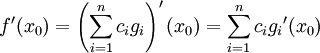• Daraus folgt nun: Die differenzierbaren Funktionen (auf einem gegebenen Intervall) bilden einen reellen Vektorraum, und die Differentiation ist eine lineare Abbildung von diesem Vektorraum in den Vektorraum aller Funktionen.

Literatur

• Heuser: Lehrbuch der Analysis - Teil 1, 6-te Auflage, Teubner 1989, ISBN 3-519-42221-2, S. 270 (Differentationregeln)

Weblinks

• Summenregel auf mathe-lexikon.at
• Summenregel auf PlanetMath (engl.)