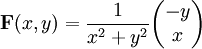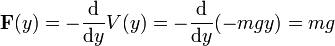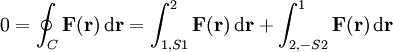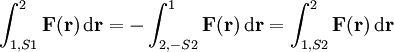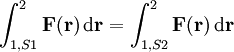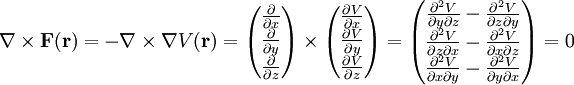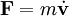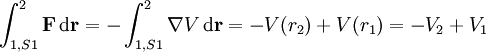- Dissipatives Kraftfeld
-
In der Physik heißt ein Kraftfeld konservativ, wenn es nur vom Ort abhängig ist und eine der drei folgenden äquivalenten Eigenschaften besitzt:
- Es gibt ein skalares Feld
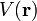 , mit
, mit 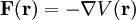 , wobei
, wobei  der Gradient ist.
der Gradient ist. - Die Arbeit
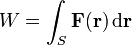 entlang eines beliebigen Weges S durch das Kraftfeld ist nur vom Anfangs- und Endpunkt des Weges, nicht aber von seinem Verlauf abhängig. Insbesondere ist die Arbeit entlang einer beliebigen geschlossenen Kurve C gleich Null, also
entlang eines beliebigen Weges S durch das Kraftfeld ist nur vom Anfangs- und Endpunkt des Weges, nicht aber von seinem Verlauf abhängig. Insbesondere ist die Arbeit entlang einer beliebigen geschlossenen Kurve C gleich Null, also 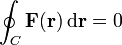
- Das Feld ist auf einem einfach zusammenhängenden Gebiet definiert und erfüllt dort die Integrabilitätsbedingung
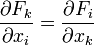 . Dies bedeutet, dass die Rotation verschwindet, also
. Dies bedeutet, dass die Rotation verschwindet, also 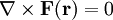
Beispiele für konservative Kräfte sind die Grundkräfte der Physik. Das Gegenteil einer konservativen Kraft ist die dissipative Kraft, die umso mehr Arbeit verrichtet, je länger der zurückgelegte Weg ist. Eine dissipative Kraft ist beispielsweise die Reibung. Die meisten physikalischen Systeme sind dissipativ, da Energie durch Reibung oder nicht-konservative Kraftfelder (Wirbelfelder) verloren geht. Allerdings kann man durch eine Erweiterung des betrachteten Systems (z. B. wenn man bei der Berücksichtigung von Reibung auch die Energieinhalte eines angekoppelten Wärmereservoirs mitberücksichtigt) jedes physikalische Ereignis in einem konservativen System beschreiben.
Inhaltsverzeichnis
Lokale Konservativität
Bei der Betrachtung der letzten dieser Eigenschaften ist Vorsicht geboten, da Kraftfelder existieren, die trotz verschwindender Rotation nicht konservativ sind. Das bekannteste Beispiel ist der stromdurchflossene Leiter, dessen Magnetfeld wie folgt aussieht:
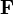 steht also senkrecht auf r, wobei x2 + y2 = r2 gilt. Zwar ist die Integrabilitätsbedingung erfüllt, jedoch existieren die Ableitungen im Nullpunkt nicht, da das Gebiet nicht einfach zusammenhängend ist. Damit handelt es sich nicht um ein Gradientenfeld, wie man auch anhand des Ringintegrals um den Einheitskreis erkennen kann. Der Einheitskreis wird parametrisiert durch
steht also senkrecht auf r, wobei x2 + y2 = r2 gilt. Zwar ist die Integrabilitätsbedingung erfüllt, jedoch existieren die Ableitungen im Nullpunkt nicht, da das Gebiet nicht einfach zusammenhängend ist. Damit handelt es sich nicht um ein Gradientenfeld, wie man auch anhand des Ringintegrals um den Einheitskreis erkennen kann. Der Einheitskreis wird parametrisiert durch
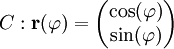 mit
mit 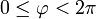 .
.
Damit ist das Ringintegral
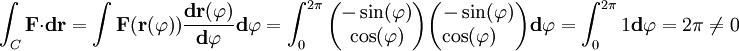 .
.
Ist ein Feld konservativ - somit verschwindet jedes Integral entlang eines geschlossenen Weges -, dann folgt daraus, dass die Rotation verschwindet (lokale Konservativität). Die Umkehrung dieser Aussage aber gilt im Allgemeinen nicht: Bei verschwindender Rotation ist das Feld nicht unbedingt konservativ.
Potential
Das skalare Feld V(r) aus dem ersten Kriterium heißt Potential oder potentielle Energie. Das Minuszeichen in diesem Kriterium ist Konvention und hat eine tiefere Bedeutung, die aber erst im Variationsprinzip der Lagrange-Mechanik offensichtlich wird und somit vorerst willkürlich wirkt. Den Grund für diese Konvention kann man sich an folgendem Beispiel klar machen: In der Nähe der Erdoberfläche ist das Gravitationspotential einer Masse m in einer Höhe h=y unter der Erdbeschleunigung g > 0 näherungsweise (d.h. unter Annahme konstanter Erdbeschleunigung für kleine y-Bereiche) V(y)= + m g y. Da Koordinatensysteme auf der Erdoberfläche nach oben positiv gezählt werden (denn einen Körper höher zu heben, heißt auch, größeres Potential aufzubauen), muss die nach unten gerichtete Erdbeschleunigung negativ sein. Wenn man also nicht nur die Beträge von g und y verwendet, sondern auch ihre entgegengesetzte Richtung berücksichtigt, so schreibt sich V(y)= - m g y mit den Vektoren g und y. Berechnet man damit anschließend die Kraft nach dem ersten Kriterium, erhält man:
Die Kraft wirkt also, wie erwartet, in Richtung Erdmittelpunkt, genau in die gleiche Richtung wie die Erdbeschleunigung g.
Beweis und Gleichheit der Kriterien
Wie anfangs bereits festgestellt, sind die drei Kriterien für ein konservatives Kraftfeld gleichbedeutend. Das erste Kriterium ist gerade die Definition eines konservativen Kraftfeldes, die anderen beiden sind lediglich andere Formulierungen des ersten Kriteriums. Oftmals werden Kraftfelder dieser Art auch direkt durch das zweite Kriterium definiert. Davon ausgehend, dass die Arbeit in einem konservativen Kraftfeld wegunabhängig ist, kann zunächst die Korrektheit des zweiten Kriteriums gezeigt werden.
Man betrachte dazu einen geschlossenen Weg C in einem konservativen Kraftfeld, der wie im Bild rechts verläuft: Von Punkt 1 über Weg S1 zum Punkt 2, dann über den Weg S2 zurück zum Punkt 1.
Das Ringintegral über diesen Weg ergibt sich damit zu
Für alle möglichen Wege S1, S2 wäre das Integral über den Weg S1 + (-S2) nur gleich Null, wenn
gilt. Also ist
was gerade der Wegunabhängigkeit und damit einer der möglichen Definitionen für ein konservatives Kraftfeld entspricht.
Das dritte Kriterium sagt aus, dass die Rotation des Kraftfeldes verschwindet. Da nach dem ersten Kriterium
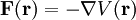 ist, gilt für die Rotation
ist, gilt für die RotationWobei der letzte Schritt wegen der Vertauschbarkeit der partiellen Ableitungen gemäß des Satzes von Schwarz zustande kam. Das erste und dritte Kriterium sind damit gleichbedeutend.
Hieraus folgt nun jedoch auch, dass diese gleichbedeutend zum zweiten Kriterium sind. Da
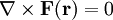 ist, gilt nach dem Satz von Stokes für eine geschlossene Kurve C, die von einer Fläche A umschlossen wird
ist, gilt nach dem Satz von Stokes für eine geschlossene Kurve C, die von einer Fläche A umschlossen wird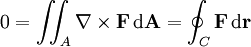 .
.
Da hier die Arbeit wieder verschwindet, was nach dem ersten Beweis die Unabhängigkeit der betrachteten Wege bedeutet, folgt schließlich die Gleichheit aller drei Kriterien.
Energieerhaltung
In der klassischen Mechanik gilt für die kinetische Energie
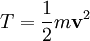 ,
,
wobei v die Geschwindigkeit ist.
Mit dem zweiten Newtonschen Axiom
für konstante Massen m kann die Energie geschrieben werden als
![E = \int_{t_1}^{t_2} \mathbf F[\mathbf r(t),\mathbf v(t),t] \, \mathbf v(t) \, \mathrm dt=\int_{t_1}^{t_2} m \dot \mathbf v(t) \, \mathbf v(t) \, \mathrm dt](/pictures/dewiki/50/299861002cf285c288dc94c04b2c9beb.png) .
.
Dann gilt für den Weg von Punkt 1 zum Punkt 2 das Wegintegral
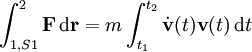 .
.
Für die rechte Seite dieser Gleichung gilt
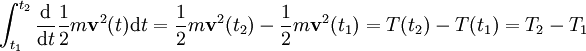 .
.
Das bedeutet, dass die gesamte Arbeit, die bei der Bewegung aufgebracht wird, der Änderung der kinetischen Energie entspricht. Für die linke Seite gilt hingegen unter Verwendung der Eigenschaften konservativer Kräfte
und damit
- T2 − T1 = − V2 + V1
bzw.
- T1 + V1 = T2 + V2
was gerade dem Energieerhaltungssatz entspricht. Die Eigenschaft der Energieerhaltung ist auch der Grund, weshalb konservative Kraftfelder ihren Namen erhielten - die Energie ist konserviert. Der Begriff der Konservativität wird ebenfalls in einem erweiterten Zusammenhang verwendet, wenn nicht die Energie, sondern eine andere physikalische Größe, wie beispielsweise die Masse, erhalten bleibt (konservativer Massenübertrag).
Siehe auch
- Es gibt ein skalares Feld
Wikimedia Foundation.