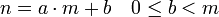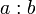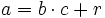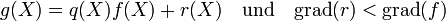Divisionsalgorithmus

Die Artikel Division mit Rest und Modulo überschneiden sich thematisch. Hilf mit, die Artikel besser voneinander abzugrenzen oder zu vereinigen. Beteilige dich dazu an der Diskussion über diese Überschneidungen. Bitte entferne diesen Baustein erst nach vollständiger Abarbeitung der Redundanz. Gunther 16:56, 2. Nov. 2006 (CET)

Die Division mit Rest oder der Divisionsalgorithmus ist ein mathematischer Satz aus der Algebra und der Zahlentheorie. Er besagt, dass es zu zwei Zahlen n und 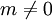$m \ne 0$ eindeutig bestimmte Zahlen a und b gibt für die

$n = a \cdot m + b \quad 0 \le b < m$

gilt. Die Zahlen a und b lassen sich durch die schriftliche Division ermitteln.

Die Division mit Rest ist auch für Polynome definiert. Die allgemeinste mathematische Struktur, in der es eine Division mit Rest gibt, ist der euklidische Ring.

Natürliche Zahlen

Wenn zwei natürliche Zahlen, der Dividend a und der Divisor b (ungleich 0), mit Rest dividiert werden sollen, also wenn

$a : b\,$

berechnet werden soll, so wird gefragt, wie man die Zahl a als Vielfaches von b und einem „kleinen Rest“ darstellen kann:

$a = b \cdot c + r$

Hier sind c der so genannte Ganzzahlquotient und r der Rest. Entscheidende Nebenbedingung ist, dass r eine Zahl in 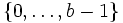$\{0, \dots, b-1\}$ ist. Hierdurch wird r eindeutig bestimmt.

Der Rest ist also die Differenz zwischen dem Dividenden und der größten Zahl, die höchstens so groß wie der Dividend und durch den Divisor teilbar ist, für die die Division also keinen Rest ergibt. Ein Rest ungleich 0 ergibt sich folglich nur, wenn zwei Zahlen nicht Vielfache voneinander sind. Man sagt auch: Der Dividend ist nicht durch den Divisor teilbar, weshalb ein Rest übrigbleibt.

Liegt der Divisor fest, so spricht man beispielsweise auch vom Neunerrest einer Zahl, also dem Rest, der sich bei Division dieser Zahl durch neun ergibt.

Beispiel

Bei einer Division durch 3 kann der Rest die Werte 0, 1 oder 2 annehmen. Sehr anschaulich wird das, wenn man die Zahlen durch Striche ersetzt:

Division 7 durch 3:

7 = |||||||
3 = |||

Jetzt kann man die 7 Striche zu Blöcken mit je 3 Strichen gruppieren:

7 = ||| ||| |

Ein dabei entstehender unvollständige 3er-Block bildet den Rest. Dieser kann aus einem oder zwei Strichen bestehen oder fehlen, wenn die Division restlos aufgeht.

Ganze Zahlen

Ist b eine negative ganze Zahl, dann gibt es keine Zahlen zwischen 0 und b-1. Stattdessen fordert man, dass der Rest zwischen 0 und |b|-1 (dem Betrag von b minus 1) liegt. Alternativ kann man aber auch verlangen, dass der Rest in diesem Fall zwischen b+1 und 0 liegt, also dasselbe Vorzeichen hat wie b. Eine dritte Möglichkeit ist, den betragskleinsten Rest zu wählen. Diese Variante liefert für a = b · c + r die beste Näherung b · c für a.

Beispiel

Dividiert man negative Zahlen, ergibt sich entsprechend der Alltagserfahrung folgendes Bild:

 7 :   3 =  2 Rest  1
−7 :   3 = −2 Rest −1

übertragen auf negative Teiler – obwohl wenig anschaulich – folgt:

 7 :  −3 = −2 Rest  1
−7 :  −3 =  2 Rest −1

(hierbei wird für die Wahl von Quotient und Rest, zunächst so getan, als gäbe es keine Vorzeichen, sie werden sozusagen nach der „eigentlichen Berechnung wieder hinzugefügt“). Als Quotient wird hier immer ein Wert bestimmt, dessen Betrag kleiner oder gleich dem Betrag des Quotienten im Bereich der rationalen Zahlen ist. Der Rest und sein Vorzeichen folgen aus der Wahl des Quotienten.

Man beachte, dass DIV- und MOD-Befehle (für ganzzahlige Division und Restbildung) in den meisten Programmiersprachen (und z. B. sogar in Intels 80x86-Prozessoren) genau diesem Alltagsansatz entsprechend implementiert sind.

Wie groß der Rest bei einer Division nun ausfällt, sei Geschmackssache, könnte man meinen, denn es steht jedem frei, nur einen Teil einer gegebenen Größe zu teilen, den verbleibenden Rest erklärt er einfach zum „Rest“. Lassen wir hierbei auch zu, dass „Schulden“ gemacht werden dürfen, sind beispielsweise alle folgenden Ergebnisse zulässig:

 7 :  3 =  1 Rest  4
 7 :  3 =  2 Rest  1
 7 :  3 =  3 Rest −2

bzw.

−7 :  3 = −1 Rest −4
−7 :  3 = −2 Rest −1
−7 :  3 = −3 Rest  2

Zur Normierung wird in der Mathematik die Konvention verwendet, die Vorzeichen der Reste aus denen der Teiler zu beziehen, wie in den folgenden Beispielen dargestellt:

 7 :   3 =  2 Rest  1
−7 :   3 = −3 Rest  2
 7 :  −3 = −3 Rest −2
−7 :  −3 =  2 Rest −1

hierbei kann die Zugehörigkeit einer Zahl zu einer Restklasse direkt am Rest abgelesen werden.

Einige Programmiersprachen und Computeralgebrasysteme tragen dieser Vielfalt von Konventionen Rechnung, indem sie zwei Modulo- oder Rest-Operatoren zur Verfügung stellen. Im Beispiel Ada hat:

• (A rem B) dasselbe Vorzeichen wie A und einen Absolutwert kleiner als der Absolutwert von B
• (A mod B) dasselbe Vorzeichen wie B und einen Absolutwert kleiner als der Absolutwert von B

Bestimmung des Restes für spezielle Teiler

Häufig kann man den Rest an der Dezimaldarstellung ablesen (die folgenden Regeln gelten nur für natürliche Zahlen):

• bei Division durch 2: der Rest ist 1, wenn die letzte Ziffer ungerade ist, und 0, wenn die letzte Ziffer gerade ist
• bei Division durch 3: der Rest ist gleich dem Rest, den die iterierte Quersumme bei Division durch 3 lässt
• bei Division durch 5: der Rest ist gleich dem Rest, den die letzte Ziffer bei Division durch 5 lässt
• bei Division durch 9: der Rest ist die iterierte Quersumme oder 0, falls diese 9 ist
• bei Division durch 10: der Rest ist die letzte Ziffer.

Ähnliche, wenn auch etwas kompliziertere Regeln existieren für etliche weitere Teiler.

Verallgemeinerung: Reelle Zahlen

Sind a und b reelle Zahlen, b ungleich 0, dann kann man eine Division mit Rest folgendermaßen definieren: Der ganzzahlige Quotient c und Rest r im halboffenen Intervall [0, |b|) sind diejenigen (eindeutig bestimmten) Zahlen, die die Gleichung a = b · c + r erfüllen.

Auch hier gibt es die Alternativen, dem Rest dasselbe Vorzeichen wie b zu geben oder den betragskleinsten Rest zu wählen. Letztere Alternative entspricht der Rundung: Die Division mit Rest von a durch 1 liefert eine ganze Zahl c und eine reelle Zahl r mit Betrag ≤ 0,5, die die Gleichung a = c + r erfüllen. Die Zahl c ist der auf ganze Zahlen gerundete Wert von a.

Beachte, dass hierbei der Quotient nicht aus derselben Menge (der reellen Zahlen) genommen wird wie Divisor und Dividend.

Polynome

Bei der Division mit Rest für Polynome muss das als Divisor auftretende Polynom f(X) aus dem Polynomring R[X] eine Voraussetzung erfüllen: Der Leitkoeffizient von f(X) muss eine Einheit von R sein (insb. ist f(X) nicht das Nullpolynom). Unter dieser Bedingung gibt es zu jedem $g(X) \in R[X]$ eindeutig bestimmte Polynome $q(X), r(X) \in R[X]$ mit

$g(X) = q(X) f(X) + r(X) \quad \text{und} \quad \operatorname{grad}(r) < \operatorname{grad}(f)$

Ein Beispiel ist das folgende Polynom.

2x² + 4x + 5 = (2x + 2)(x + 1) + 3

Die Polynome q(X) und r(X) lassen sich durch Polynomdivision bestimmen.