Divisionsring

Ein Schiefkörper oder Divisionsring ist eine Menge mit zwei zweistelligen Verknüpfungen „+“ und „·“, die alle Eigenschaften eines Körpers besitzt, außer dass die Multiplikation nicht notwendigerweise kommutativ ist.

Ein Schiefkörper ist somit ein Ring mit Einselement 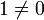$1\neq0$, in dem jedes Element 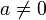$a\neq0$ ein Inverses a ^{− 1} besitzt, so dass $a \cdot a^{-1}=a^{-1} \cdot a = 1$.

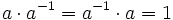Alle Schiefkörper mit einer endlichen Anzahl von Elementen sind nach dem Satz von Wedderburn zugleich Körper. Ist ein Schiefkörper kein Körper, muss er demnach aus unendlich vielen Elementen bestehen. Ein Beispiel ist der Schiefkörper der Quaternionen.

Das Zentrum eines Schiefkörpers S ist ein (kommutativer) Körper K, und mittels der Inklusion wird S zu einer K-Algebra. Die Gesamtheit derjenigen Schiefkörper mit einem vorgegebenen Zentrum K, die als K-Vektorraum endlichdimensional sind, wird durch die Brauergruppe von K beschrieben.

Ähnliche Begriffe

In einer Divisionsalgebra muss die Multiplikation nicht notwendigerweise assoziativ sein.