Satz von Artin-Wedderburn

Als halbeinfach bezeichnet man in der Mathematik bestimmte Strukturen, die auf vergleichsweise leicht verständliche Weise aus „Grundbausteinen“ zusammengesetzt sind.

Der Begriff wird im mathematischen Gebiet der Algebra in unterschiedlichen Zusammenhängen benutzt. Besondere Bedeutung hat er in der Theorie der Moduln und Ringe. Die „Grundbausteine“ sind hier die „einfachen Moduln“. Halbeinfache Moduln sind dann gewissermaßen die nächste Stufe, nämlich solche, die aus einfachen Moduln „zusammengesetzt“ sind. Für diesen „Aufbau“ ist das Konzept der direkten Summe entscheidend. Über halbeinfache Moduln (und Ringe) sind viele Sätze bekannt, sie sind mathematisch gesehen also, wie der Name andeutet, immer noch recht „einfache“ Objekte.

Eine der wichtigsten Anwendungen liegt in der Darstellungstheorie von Gruppen und basiert auf dem Satz von Maschke.

Halbeinfache Moduln

(Im Folgenden wird Vertrautheit des Lesers mit dem Begriff des Moduls vorausgesetzt.)

Sei M ein Modul über einem Ring (mit Eins) R.

M heißt einfach oder irreduzibel, falls 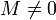$M \neq 0$ und M keine Untermoduln außer sich selbst und den Nullmodul enthält.

M heißt halbeinfach oder vollständig reduzibel, wenn eine der folgenden äquivalenten Bedingungen erfüllt ist:

1. M lässt sich als direkte Summe von irreduziblen Moduln schreiben.
2. M lässt sich als Summe von irreduziblen Moduln schreiben.
3. Existenz von Komplementen: Für jeden Untermodul N von M existiert ein Untermodul P von M, so dass $M=N\oplus P$.

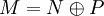Eigenschaften

• Untermoduln, Quotientenmoduln und direkte Summen von halbeinfachen Moduln sind halbeinfach.
• Dichtesatz (Jacobson)
• Ein Modul ist einfach genau dann, wenn jedes Element 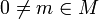$0 \neq m \in M$ schon M erzeugt (als Modul).

Halbeinfache Ringe

Jeder Ring R wirkt auf sich selbst durch Multiplikation von links und wird so zu einem Linksmodul über sich selbst. Die Untermoduln sind dann genau die Linksideale. Die irreduziblen Untermoduln sind genau die nichttrivialen minimalen Linksideale. Natürlich kann man analog R zu einem Rechtsmodul über sich selbst machen.

Ein Ring heißt halbeinfach, wenn er als Modul über sich selbst halbeinfach ist. Man kann zeigen, dass dies nicht davon abhängt, ob man R als Links- oder Rechtsmodul betrachtet.

Bemerkung: Ein Ring heißt einfach, wenn er keine nichttrivialen beidseitigen Ideale besitzt. Nicht jeder einfache Ring ist halbeinfach.

Eigenschaften

• Ist R halbeinfach, so ist jeder R-Modul halbeinfach. Dies folgt aus obigen Eigenschaften von halbeinfachen Moduln und aus der Tatsache, dass jeder Modul ein Quotient eines freien Moduls (also einer direkten Summe von Kopien von R) ist.

Satz von Artin-Wedderburn

Jeder halbeinfache Ring ist isomorph zu einem (endlichen) Produkt von Matrizenringen über Schiefkörpern (Divisionsringen). Hierbei ist der ganze Matrizenring gemeint, nicht ein Unterring.

Beispiel

Sei G eine endliche Gruppe und K ein Körper. Sei K[G] die Gruppenalgebra (dabei handelt es sich um den K-Vektorraum mit Basis G und der Multiplikation, die durch die Gruppenstruktur induziert wird). Die Darstellungen von G in K-Vektorräumen entsprechen genau den K[G]-Moduln. Unterdarstellungen entsprechen Untermoduln, und irreduzible Darstellungen entsprechen irreduziblen Moduln.

Sei nun K so, dass die Charakteristik von K nicht | G | teilt (z.B. 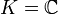$K=\mathbb{C}$). Dann besagt der Satz von Maschke, dass jeder K[G]-Modul halbeinfach ist.

Literatur

• Serge Lang, Algebra
• Nathan Jacobson, Basic Algebra II