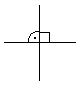Drehwinkel

Ein Winkel ist in der Geometrie ein Teil der Ebene, der von zwei in der Ebene liegenden Strahlen (Halbgeraden) mit gemeinsamem Anfangspunkt begrenzt wird.

Der gemeinsame Anfangspunkt der beiden Strahlen wird Scheitelpunkt des Winkels, Winkelscheitel oder kurz „Scheitel“ genannt; die Strahlen heißen Schenkel des Winkels. Ein Winkel kann durch drei Punkte festgelegt werden, von denen einer im Scheitel des Winkels liegt und die beiden anderen auf je einem Schenkel des Winkels.

Die physikalische Größe, die die relative Lage der Strahlen zueinander beschreibt, wird als Winkelweite, Drehwinkel oder Winkelabstand (Winkeldistanz) bezeichnet, üblicherweise auch verkürzend als „Winkel“, wenn eine Unterscheidung von dem geometrischen Objekt nicht notwendig ist, beispielsweise in der Physik. Die Größe des Winkels wird mit einem Winkelmaß angegeben.

Die Winkelweite kann auch als Maß einer ebenen Drehung definiert werden.

Zur Unterscheidung vom Raumwinkel wird der hier definierte Winkel auch als ebener Winkel bezeichnet.

Definition

In der Geometrie sind zur Definition des Winkels als Objekt verschiedene Ansätze möglich. Dabei lassen sich zwei Typen unterscheiden:

• Der ungerichtete Winkel, der durch eine vorzeichenlose Winkelweite gekennzeichnet ist.
• Der gerichtete Winkel, der über eine Orientierung verfügt, und als Drehwinkel oder Winkelabstand gemessen wird.

Darstellung als Strahlenpaar

Die eingangs angeführte Definition zweier von einem Punkt ausgehenden Strahlen ist in die Anwendungen wie etwa die Koordinatensysteme und deren Achsen eingebunden.

Darstellung als Halbgeradenpaar

Der Winkel ist ein geometrisches Gebilde zweier Halbgeraden.

Seien f, g zwei Geraden, die sich in einem Punkt S schneiden, so teilt der Punkt S die Geraden f, g in Halbgeraden. Je eine Halbgerade von f und g (die Schenkel) zusammen mit S (den Scheitel) bilden einen Winkel.

Über die „ursprünglichen“ Geraden ermöglicht diese Darstellung etwa Betrachtungen über die verschiedenen Winkelpaare.

Darstellung als Teil der Ebene

Der Winkel ist ein Teilbereich der Zeichenebene, der von zwei Halbstrahlen oder Halbgeraden begrenzt wird. Diese bilden den Rand, und der Rest des Bereiches das Innere.

Die Definition wird im Schulunterricht verwendet und betont das „Körperhafte“ des Gebildes, und dient – über die Festlegung eines Innen- und Außenraums – der Einführung in die Trigonometrie: Das Dreieck lässt sich als Schnittmenge zweier Winkel mit einem gemeinsamen Schenkel definieren.

Ad hoc ist bei diesen drei Ansätzen der Winkel ein ungerichteter Winkel, erst eine zusätzliche Auszeichnung einer der beiden Halbstrahlen oder Halbgeraden als die „erste“ ermöglicht die Angabe eines gerichteten Winkels.

Darstellung als Drehung

Drehwinkel

Man kann auch sagen, dass ein Winkel durch eine Drehung eines Strahls oder einer Halbgeraden in einer Ebene um seinen bzw. ihren Anfangspunkt entsteht.

Da es zwei verschiedene Möglichkeiten gibt, den Strahl zu drehen, muss zusätzlich die Drehrichtung angeben werden:

• Linksdrehung, gegen den Uhrzeigersinn, auch mathematisch positiver Drehsinn genannt (Winkel ist positiv). grün dargestellt
• Rechtsdrehung, mit dem Uhrzeigersinn, auch mathematisch negativer Drehsinn genannt (Winkel ist negativ). blau dargestellt

In der Mathematik ist es üblich, die Drehung gegen den Uhrzeigersinn – also im mathematisch positiven Drehsinn – auszuführen. Wenn die Drehung andersherum erfolgen soll, sollte dieses ausdrücklich angegeben werden.

In der Geodäsie (Vermessungswesen) wird der Winkel im Uhrzeigersinn, also rechtsdrehend von 0 Gon bis 400 Gon gezählt. Da es in der Geodäsie per Definition keine negativen Winkel gibt, ist der Drehsinn positiv. Analog zur Uhr, auch hier wird von 0 bis 24 h positiv, rechtsdrehend gezählt. Alle geodätischen Messinstrumente werden zur Richtungs- oder Winkelmessung rechtsherum gedreht.

Bezeichnung von Winkeln

∡

∠

Die Angabe eines Winkels erfolgt nach DIN 1302 oder ISO 31-11:

• Winkel werden meistens mit kleinen griechischen Buchstaben, z. B. α oder β, bezeichnet.
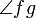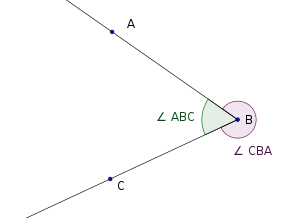
• Ein Winkel $\angle fg$ ist ein Winkel zwischen zwei Halbstrahlen, Geraden, Kanten und ähnlichem. Er wird dann von f ausgehend Richtung g gezählt.
• Alternativ kann man die drei Punkte angeben, die den Winkel definieren, wobei der Scheitelpunkt immer in der Mitte steht, z. B. Winkel ABC, 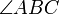$\angle ABC$ oder veraltend 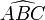$\widehat {ABC}$. Dies bezeichnet den Winkel zwischen [BA] und [BC], wobei [BA] im mathematisch positiven Drehsinn auf [BC] gedreht wird.
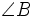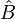• Im englischen Sprachraum ist auch nur die Angabe des Scheitels $\angle B$ bzw. $\hat {B}$ üblich.

Für den Formelsatz steht das Zeichen »∠« (HTML ∠/∠, TeX \angle, Unicode U+2221) zur Verfügung, für den gerichteten Winkel auch »∡« (TeX \measuredangle, U+2220 MEASURED ANGLE, keine HTML-Entity), die sich beide im Unicode-Block Mathematische Operatoren finden. Das liegende Winkelzeichen entspricht den angloamerikanischen Gewohnheiten, im europäischen Formelsatz ist ein Zeichen üblich, das dem amerikanischen »∢« U+2222 für den Raumwinkel zum Verwechseln ähnlich sieht. »∠« findet auch für Neigung und Winkligkeit (Lagetoleranz, DIN EN ISO 1101) Verwendung. Speziell für den rechten Winkel verwendet man »∟«, einen punktierten Winkel, in der Technik auch ein Quadrat, oder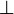 $\perp$.

Winkelmaße und Maßeinheiten für Winkel

Ausführliche Informationen bietet der Hauptartikel Winkelmaß, Umrechnungen sind bei den einzelnen Maßen zu finden.

Winkelmaß	Maßeinheit	1 Vollwinkel =	Einheitenzeichen
-	Vollwinkel	1
Bogenmaß	Radiant	2π	rad
Gradmaß	Grad (Bogenminute, Bogensekunde)	360	° ( ′ ″ )
Geodätisches Winkelmaß	Gon (veraltet: Neugrad)	400	gon
Zeitmaß	Stunden, Minuten, Sekunden	24	h ′ ″
-	Nautischer Strich	32	¯
-	Artilleristischer Strich (Schweiz: Artilleriepromille)	6400	mil ( A‰ )
-	Prozent, Promille	nichtlinear	%, ‰

Weitere Formen der Angabe eines Winkels:

• Der Tangens der Winkelweite des Steigungswinkels (auch Steigungsmaß genannt, entspricht der Maßangabe in Prozent)
• Ein Paar (x, y) mit Cosinus und Sinus (entspricht den kartesischen Koordinaten des Punktes auf dem Einheitskreis)

Arten von Winkeln

spitzer Winkel

kleiner ¼ Vollwinkel: (0°, < 90°) = (0^g, < 100^g) = (0, < ½·π);

rechter Winkel

gleich ¼ Vollwinkel: 90° = 100^g = ½·π;

stumpfer Winkel

größer ¼ und kleiner ½ Vollwinkel: (> 90°, < 180°) = (> 100^g, < 200^g) = (> ½·π, < π);

gestreckter Winkel

gleich ½ Vollwinkel: 180° = 200^g = π;

überstumpfer (erhabener) Winkel

größer ½ und kleiner 1 Vollwinkel: (> 180°, < 360°) = (>200^g, < 400^g) = (> π, < 2·π);

voller Winkel (Vollwinkel)

360° Winkel

Vollwinkel und Rechter Winkel

Rechter Winkel, Kennzeichnung

• Einen 360°-Winkel nennt man auch Vollwinkel oder Vollkreis.
• Einen 90°-Winkel nennt man auch rechter Winkel.

Zwischen zwei sich schneidenden Geraden gibt es vier Winkel. Jeweils zwei nebeneinander liegende summieren sich dabei zu 180°. Der rechte Winkel hat die Besonderheit, dass diese beiden Winkel genau gleich sind. Jeweils zwei gegenüberliegende Winkel sind gleich. Der Vollwinkel hat die Besonderheit, dass zwei der Winkel null sind.

Zwei Geraden oder Strecken, die sich im rechten Winkel schneiden, nennt man zueinander orthogonal. In einer Zeichnung wird der rechte Winkel durch einen Viertelkreis mit Punkt oder durch ein Quadrat dargestellt.

Der Vollwinkel ist in Deutschland eine gesetzliche Einheit im Messwesen, er besitzt kein Einheitenzeichen.

Spezielle Winkelpaare

Die Geometrie kennt besondere Bezeichnungen für Paare von Winkeln, die zueinander in einer besonderen Beziehung stehen. Die für solche Winkel geltenden Gesetze helfen bei der Untersuchung komplexerer geometrischer Objekte.

Komplement- oder Komplementärwinkel

Supplement- oder Ergänzungswinkel

Komplementwinkel oder Komplementärwinkel

Zwei Winkel heißen Komplementwinkel, wenn sie sich zu einem rechten Winkel (90°) ergänzen.

Supplementwinkel oder Ergänzungswinkel

Zwei Winkel heißen Supplementwinkel (auch: Supplementärwinkel), oder kurz E-Winkel, wenn sie sich zu 180° ergänzen.

Nebenwinkel

Nebenwinkel

Schneiden sich zwei Geraden, so bezeichnet man ein Paar benachbarter Winkel als Nebenwinkel.

Nebenwinkel ergänzen sich zu 180°.

Sie sind also Supplementwinkel.

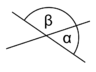
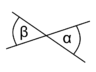
Scheitelwinkel oder Gegenwinkel

Scheitelwinkel

Schneiden sich zwei Geraden, so bezeichnet man das Paar gegenüberliegender Winkel als Scheitelwinkel oder Gegenwinkel.

Scheitelwinkel sind immer gleich groß.

Die Bezeichnung Scheitelwinkel kommt daher, dass die beiden Winkel durch Punktspiegelung am Scheitelpunkt aufeinander abgebildet werden.

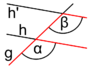
Wechselwinkel oder Z-Winkel

Wechsel- oder Z-Winkel

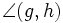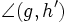Schneidet eine Gerade g zwei Geraden h und h', so heißen die Winkel $\angle(g,h)$ und $\angle(g,h')$, die auf unterschiedlichen Seiten von g und unterschiedlichen Seiten von h bzw. h' liegen, Wechsel- oder Z-Winkel. Für den Fall der Parallelität der Geraden h und h' gilt:

Wechselwinkel an Parallelen sind gleich groß.

Aus der Winkelgleichheit kann umgekehrt auf die Parallelität von Geraden geschlossen werden: Wird ein Geradenpaar h, h' von einer weiteren Geraden g so geschnitten, dass die Schnittwinkel auf unterschiedlichen Seiten von g und unterschiedlichen Seiten von h bzw. h' gleich groß sind, so sind die Geraden h und h' parallel.

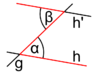
Stufenwinkel oder F-Winkel

Stufen- oder F-Winkel

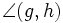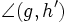Schneidet eine Gerade g zwei Geraden h und h', so heißen die Winkel $\angle(g,h)$ und $\angle(g,h')$, die auf derselben Seite von g und beide entweder ober- oder unterhalb von h bzw. h' liegen, Stufen- oder F-Winkel. Für den Fall der Parallelität der Geraden h und h' gilt:

Stufenwinkel an Parallelen sind gleich groß.

Aus der Winkelgleichheit kann umgekehrt auf die Parallelität von Geraden geschlossen werden: Wird ein Geradenpaar h, h' von einer weiteren Geraden g so geschnitten, dass die Schnittwinkel auf derselben Seite von g und jeweils ober- oder unterhalb von h und h' gleich groß sind, so sind die Geraden h und h' parallel.

Nachbarwinkel oder E-Winkel

Nachbar- oder E-Winkel

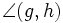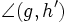Schneidet eine Gerade g zwei weitere parallele Geraden h und h', so bezeichnet man die Winkel $\angle(g,h)$ und $\angle(g,h')$, die auf derselben Seite von g, aber auf unterschiedlichen Seiten von h und h' liegen, als Nachbar- oder E-Winkel.

Nachbarwinkel ergänzen sich zu 180°.

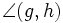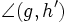Aus der Ergänzung der Winkel zu 180° kann umgekehrt auf die Parallelität von Geraden geschlossen werden: Wird ein Geradenpaar h, h' von einer weiteren Geraden g so geschnitten, dass sich die Schnittwinkel $\angle(g,h)$ und $\angle(g,h')$, die auf derselben Seite von g, aber jeweils auf unterschiedlichen Seiten von h und h' liegen, zu 180° ergänzen, so sind die Geraden h und h' parallel.

Die Eigenschaft, dass sich Nachbarwinkel zu 180° ergänzen, folgt direkt aus dem Parallelenaxiom der euklidischen Geometrie. Die folgenden Eigenschaften von Stufen- und Wechselwinkeln lassen sich aus der Betrachtung von Neben- und Scheitelwinkeln von Nachbarwinkeln herleiten.

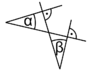
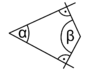
Winkel mit paarweise rechtwinkligen Schenkeln

Winkel mit paarweise rechtwinkligen Schenkeln a)

Winkel mit paarweise rechtwinkligen Schenkeln b)

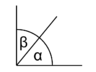
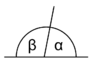
Winkel, deren Schenkel paarweise senkrecht aufeinander stehen, sind gleich groß oder ergänzen sich zu 180°. Vergleiche nebenstehende Abbildungen.

Winkelkonstruktion

Einige Winkel kann man allein mit Zirkel und Lineal konstruieren. Dazu gehören der 90 Grad-, 60 Grad-, 72 Grad- und 54 Grad-Winkel, sowie sämtliche Winkel, die durch Verdoppelung, Halbierung, Addition oder Subtraktion (siehe unten) dieser Winkel entstehen.

Die Aussage, jeder Winkel kann allein mit Hilfe von Zirkel und Lineal gedrittelt werden, gilt im Allgemeinen nicht!

Konstruktion des 90-Grad-Winkels (rechten Winkels)

Man konstruiert genauer gesagt die Senkrechte zu einer bereits gegebenen Strecke.

Konstruktion

Zeichne eine Gerade g. Wähle einen Punkt P auf g. Zeichne einen Kreis um P mit beliebigem Radius r. Dieser Kreis schneidet g in zwei Punkten, bspw. A und B. Zeichne um diese beiden Punkte jeweils einen Kreis mit einem Radius größer als r. Verbinde die beiden Schnittpunkte dieser Kreise und verlängere sie in beide Richtungen. Die entstandene Gerade schneidet g im rechten Winkel und zwar genau im Punkt P.

Ratschlag

Man braucht die Kreise nicht ganz zu schlagen; es reicht jeweils einen Bogenabschnitt zu ziehen, auf dem der Schnittpunkt liegt. Die Schnittpunkte liegen genau über (bzw. unter) dem Scheitelpunkt in senkrechter Verbindung zur gegebenen Strecke.

Daumenregel fürs Zeichnen

Je größer die Radien der Kreise, desto genauer wird der rechte Winkel.

Folgerung (Streckenhalbierung, Mittelsenkrechte)

Man halbiert eine gegebene Strecke, in dem man Kreise, deren Radius größer ist als die Hälfte der Strecke, um die Endpunkte dieser Strecke zieht. Verbindet man nun die Schnittpunkte, die beide Kreise miteinander haben, so schneidet diese Verbindungslinie die Gerade genau in der Mitte und im rechten Winkel. Infolgedessen wurde eine Mittelsenkrechte konstruiert.

Konstruktion eines 60-Grad-Winkels

Man konstruiert um den Scheitelpunkt auf einer gegebenen Strecke einen Kreis und trägt ausgehend vom Schnittpunkt zwischen Kreis und Strecke einmal den Radius des Kreises auf dem Kreis selbst ab. Die Verbindung zwischen Scheitelpunkt und dem so konstruierten Schnittpunkt schließt mit der gegebenen Gerade einen 60-Grad-Winkel ein.

Konstruktion

Man nehme einen beliebigen Abstand in den Zirkel, steche im Scheitelpunkt ein und schlage einen Kreis. Den Abstand behalte man im Zirkel und steche dann im Schnittpunkt zwischen Kreis und gegebener Gerade ein und zeichne einen weiteren Schnittpunkt mit dem Kreis.

Man verbinde diesen Schnittpunkt und den Scheitelpunkt durch eine Linie mittels Lineal.

Folgerung (Konstruktion gleichseitige Dreiecke)

Verbindet man zusätzlich den im ersten Schritt konstruierten Schnittpunkt auf der gegebenen Strecke mit dem zuletzt konstruierten Schnittpunkt, so erhält man ein gleichseitiges Dreieck. Dieses hat folglich drei gleichgroße Winkel von je 60 Grad.

Muss man also ein gleichseitiges Dreieck aus gegebener Seitengröße konstruieren, so zeichne man eine Linie, nehme die Seitengröße in den Zirkel, und schlage um einen beliebigen Punkt auf der Linie einen Kreis. Man sticht auf dem Schnittpunkt zwischen Kreis und Linie ein und trägt so die Seitenlänge auf dem Kreis selbst ab. Nun verbinde man den zuletzt konstruierten Punkt mit beiden Einstichpunkten.

Folgerung (Konstruktion von Sechsecken)

Trägt man auf einem beliebigen Kreis den Radius, den der Kreis selbst hat, mit dem Zirkel ab, so erhält man, wenn man alle auf dem Kreis nebeneinanderliegenden Schnittpunkte durch eine Gerade verbindet, ein regelmäßiges Sechseck (Hexagon)).

Dieses liegt daran, dass wenn man den Kreismittelpunkt mit den Ecken des Sechsecks verbindet jeweils 6 gleichseitige Dreiecke erhält, deren Winkel am Kreismittelpunkt jeweils 60 Grad betragen. 6·60° = 360°, also ein Kreis gleichschenkliger Dreiecke, deren Besonderheit ist, auch noch gleichseitig zu sein.

Konstruktion eines 72- oder 54-Grad-Winkels

Für die etwas exotischere Konstruktion des 72°- oder des 54°-Winkels konstruiert man ein regelmäßiges Fünfeck.

Addition und Subtraktion von Winkeln

Jeder Winkel lässt sich zu einem anderen Winkel konstruktiv addieren. Hierfür sticht man in den Punkt beim zu addierenden Winkel ein und schlägt einen Bogen, so dass er die Schenkel des Winkels schneidet. Der Radius des Bogens muss im Zirkel behalten werden; man schlägt nun einen Kreis (oder je nach Winkelgröße auch nur einen abzuschätzenden Bogen) um den Punkt bei dem Winkel, zu dem man addieren möchte, so dass dieser einen Schenkel ebendieses Winkels schneidet. Daraufhin sticht man in den Schnittpunkt des Bogens mit einem der Schenkel des zu addierenden Winkels ein und spannt diesen bis zum anderen Schenkel. Dieser Abstand wird wieder beibehalten, man schlägt nun einen Kreis um den Schnittpunkt des Bogens mit dem Schenkel des Winkels, zu dem man addieren möchte. Der Schnittpunkt der beiden Bögen wird mit dem Punkt beim Winkel, zu dem man addieren möchte, verbunden, und erhält so die Summe der beiden Ausgangswinkel.

Ebenso verhält es sich mit der Subtraktion eines Winkels, nur dass hierbei der Winkel eben nicht an den Winkel zusätzlich angetragen wird, sondern so, dass der neue Schenkel zwischen die Ausgangsschenkel des Winkels, von dem man subtrahieren möchte, liegt.

Winkelhalbierung

Ein Winkel besteht stets aus zwei Schenkeln, die sich im Scheitelpunkt treffen. Zieht man nun zwei gleichgroße Kreise auf je einem Schenkel durch den Scheitelpunkt, so bildet die Strecke zwischen den Kreisschnittpunkten die Winkelhalbierende. Jeder Punkt auf der Winkelhalbierenden ist gleich weit von den Schenkeln entfernt.

Konstruktion

Man nehme einen Abstand in den Zirkel und steche am Scheitelpunkt ein. Man zeichne so die Schnittpunkte mit den beiden Schenkeln ein. Nun behält man den Abstand im Zirkel, sticht an je einem der Schnittpunkte ein und schlägt um sie je einen Kreis. Man verbinde beide Schnittpunkte durch eine Linie mit dem Lineal und erhält so die Winkelhalbierende.

Folgerung (allgemeine Winkelkonstruktionen)

Konstruiert man die obigen Winkel (90°, 60°, 72° oder 54° oder deren Summen bzw. Differenzen), so lassen sich aus diesen per Winkelhalbierung weitere Winkel (45°, 30°, 36° und 27° oder den zugehörigen Summen bzw. Differenzen) konstruieren, die und deren Abkömmlinge sich wieder halbieren lassen. Generell lassen sich alle ganzzahligen Winkel konstruieren, die ein Vielfaches von 3° sind.

Winkelmessung

Hauptartikel: Winkelmessung

Weblinks

Winkel für Schüler erklärt