Dreiteilung

Unter der Dreiteilung des Winkels (auch: Trisektion des Winkels) versteht man in der Geometrie das Problem, ob man einen beliebigen Winkel nur mit Hilfe von Zirkel und Lineal (den euklidischen Werkzeugen) konstruktiv und präzise in drei gleich große Winkel unterteilen kann. Die Dreiteilung des Winkels gehört zu den drei klassischen Problemen der antiken Mathematik.

Drittelung von 180° (∢ AMC) in 60° (∢ BMC) und 120° (∢ AMB)

Bei speziellen Winkeln ist die Dreiteilung des Winkels möglich, etwa bei jedem ganzzahligen Vielfachen von 90°. Schon die alten Griechen versuchten vergeblich, eine allgemeine Lösung für beliebige Winkel zu finden. Um das Jahr 1830 schuf der französische Mathematiker Évariste Galois die Grundlagen, mit denen später bewiesen wurde, dass dies nicht allgemein möglich ist. Beispielsweise ist es nicht möglich, den konstruierbaren Winkel 60° zu dritteln, da 20° nicht konstruierbar ist.

Eine Dreiteilung ist nur möglich, wenn man andere Hilfsmittel verwendet als Zirkel und Lineal – etwa die Quadratrix – oder wenn man auf dem Lineal Markierungen anbringt. Andererseits kann man mit Zirkel und Lineal beliebig gute Näherungslösungen angeben.

Verallgemeinerung

Eine Verallgemeinerung des Problems ist es, genau zu charakterisieren, welche Winkel konstruierbar sind und welche nicht. Äquivalente Fragestellungen sind, für welche natürlichen Zahlen n man einen Kreis (einen Kuchen) in n gleich große Stücke mittels Zirkel und Lineal unterteilen kann bzw. welche regulären n-Ecke man konstruieren kann. Die exakte Charakterisierung der konstruierbaren n-Ecke wurde 1837 von Pierre Wantzel (nach wesentlichen Vorarbeiten von Carl Friedrich Gauß und Évariste Galois) erzielt und besagt, dass dies genau dann der Fall ist, wenn n ein Produkt aus einer Zweierpotenz und untereinander verschiedenen fermatschen Primzahlen ist. Der erste entscheidende Schritt über die Mathematik des Altertums hinaus war dem jungen Gauß mit seiner Entdeckung zu verdanken, dass das reguläre Siebzehneck konstruierbar ist. Die bekannten Fermatschen Primzahlen sind 3, 5, 17, 257 und 65537. Allgemein sind Fermat-Zahlen die Zahlen 2^m + 1, wobei m = 2^q selbst eine Zweierpotenz ist. Man vermutet, dass die Fermat-Zahlen mit q > 4 keine Primzahlen sind und weiß es für viele q.

Für das Problem der Winkeldreiteilung braucht man die fortgeschrittenen Theorien von Gauß und Galois nicht. Hier genügt die Erkenntnis, dass eine Streckenlänge, die einer irreduziblen Gleichung dritten Grades genügt, nicht konstruierbar ist; denn jede konstruierbare Streckenlänge lässt sich algebraisch durch die aufeinanderfolgende Lösung quadratischer Gleichungen gewinnen, ist also algebraisch von einem Zweierpotenzgrad.

Die Methode des Archimedes

Die Winkeldreiteilung nach Archimedes: α = 3β

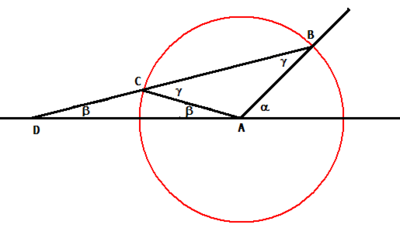
Archimedes war ein Pragmatiker, er hatte eine Lösung gefunden. Sei α der dreizuteilende Winkel wie in nebenstehender Zeichnung. Gehe dann wie folgt vor:

1. Schlage einen Kreis um A mit irgendeinem Radius r.
2. Am Lineal bringe zwei Markierungen im Abstand r an.
3. Lege das Lineal so an B, dass eine der beiden Markierungen auf der Geraden AD im Punkt D und die andere auf der Kreislinie im Punkt C liegt, und zeichne die Strecke $\overline{BD}$.
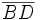4. Der Winkel β bei D ist der gesuchte Drittelwinkel.

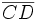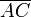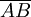Zur Begründung beachte man, dass wegen der speziellen Positionierung des Lineals die Länge der Strecke $\overline{CD}$ gleich dem Abstand r der Markierungen ist, also gleich dem Radius des Kreises, der sich auch als $\overline{AC}$ und $\overline{AB}$ wiederfindet. Insbesondere ist das Dreieck ACD gleichschenklig, weshalb der Winkel β auch bei A auftritt. Der Winkel des Dreiecks ACD bei C ist einerseits gleich 180^o − 2β (Winkelsumme im Dreieck), andererseits der Nebenwinkel von γ, also ist γ = 2β. Da das Dreieck ABC ebenfalls gleichschenklig ist, taucht der Winkel γ auch bei B auf, und der Winkel dieses Dreiecks bei A ist gleich 180^o − 2γ. Beachtet man nun, dass sich die Winkel bei A zu 180^o aufaddieren, ergibt sich α = 180^o − (180^o − 2γ) − β = 2γ − β = 3β.

Dass mit dieser Methode jeder Winkel wie bewiesen dreigeteilt werden kann, steht nicht im Widerspruch zur Unlösbarkeit des klassischen Problems, denn die obige Konstruktion wurde nicht nach den klassisch erlaubten Regeln durchgeführt. Eine Markierung am Lineal und ein geschicktes Anlegen des Lineals sind nicht erlaubte Konstruktionsmethoden. Es wurde also ein abweichender Instrumentensatz verwendet und die möglichen Konstruktionen sind vom Instrumentensatz abhängig.

Siehe auch

• Konstruierbare Polygone

Weblinks

• Eric W. Weisstein: Angle Trisection auf MathWorld (englisch)