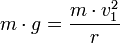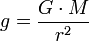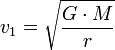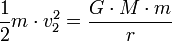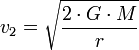Dritte kosmische Geschwindigkeit

Als kosmische Geschwindigkeiten, auch astronautische Geschwindigkeiten, werden einige Geschwindigkeitswerte bezeichnet, die in der Raumfahrtphysik eine besondere Bedeutung haben.

Bez.	v in km/s	vopt in km/s
1.	7,9	7,4
2.	11,2	10,7
3.	42,1	12,3
4.	320	100

Die Tabelle fasst die kosmischen Geschwindigkeiten 1 bis 4 zusammen. Die Werte verringern sich, wenn man die Rotationsgeschwindigkeit der Erde am Äquator oder die Bahngeschwindigkeit des Systems nutzen kann.

Erste kosmische Geschwindigkeit oder Kreisbahngeschwindigkeit

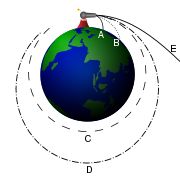
Als erste kosmische Geschwindigkeit oder Kreisbahngeschwindigkeit wird die Geschwindigkeit bezeichnet, bei der ein tangential zu einer Planetenoberfläche bewegter Satellit gerade nicht mehr auf den Planeten zurückfällt, sondern sich auf einer niedrigstmöglichen Kreisbahn um den Planeten bewegt. Die Kreisbahngeschwindigkeit folgt aus dem Gleichsetzen von Gravitationskraft und Zentripetalkraft:

Bei einer Satellitenmasse m und einem Abstand vom Planetenmittelpunkt r ergibt sich

$m \cdot g = \frac{ m \cdot v_1^2}{r}$

mit der Schwerebeschleunigung

$g = \frac{ G \cdot M }{r^2}$

wobei G die Gravitationskonstante und M die Planetenmasse ist. Daraus ergibt sich die Kreisbahngeschwindigkeit zu

$v_1 = \sqrt{\frac{ G \cdot M }{r}}$

Die Kreisbahngeschwindigkeit ist unabhängig von der Masse des Satelliten. Für die Erde beträgt sie etwa 7,9 km/s^[1], wenn als Bahnradius der Erdradius angesetzt wird. Die Umlaufperiode um die Erde ist gerade die Schuler-Periode.

Bei Satellitenstarts von der Erde muss dabei beachtet werden, dass ein Teil dieser Geschwindigkeit bereits von der Erdrotation aufgebracht wird, abhängig von der geographischen Breite des Startorts und der Startrichtung des Satelliten. Im Idealfall (Start am Äquator in Richtung Osten) beträgt dieser Beitrag 0,46 km/s.

Die Kreisbahngeschwindigkeit um die Erde ist ein hypothetischer Wert für eine Bahnhöhe von Null. Aufgrund der Reibung an der Atmosphäre haben Erdsatelliten eine Bahnhöhe von mindestens ca. 150 km über der Erdoberfläche. Die dazu notwendige Kreisbahngeschwindigkeit verringert sich entsprechend.

Zweite kosmische Geschwindigkeit oder Fluchtgeschwindigkeit

Ein Satellit mit der 1. kosmischen Geschwindigkeit beschreibt die Bahn C. Eine größere Geschwindigkeit bewirkt die Bahn D. Bei Erreichen der 2. kosmischen Geschwindigkeit entfernt sich der Flugkörper auf der Parabelbahn E.

Parabel als Grenzfall der Ellipse

Hat der Satellit eine größere Geschwindigkeit als die seiner Flughöhe entsprechende Kreisbahngeschwindigkeit, verformt sich seine Flugbahn zu einer Ellipse (hier bleibt nur der einfache Fall des waagerechten Abschusses betrachtet, die Fluchtgeschwindigkeit bleibt aber prinzipiell von der Abschussrichtung unabhängig) mit größerer Exzentrizität. Im Grenzfall liegt der erdferne Punkt der Umlaufbahn im Unendlichen, so dass der Satellit sich nicht mehr auf einer geschlossenen elliptischen Umlaufbahn befindet, sondern sich auf einer Parabelbahn von der Erde entfernt. Die hierzu notwendige Geschwindigkeit wird als zweite kosmische Geschwindigkeit, Fluchtgeschwindigkeit oder Entweichgeschwindigkeit bezeichnet. Bei einer Überschreitung dieser Geschwindigkeit nimmt die Flugbahn die Form eines Hyperbelasts an.

Herleitung nach der Potentialtheorie

Um das Gravitationsfeld verlassen zu können, muss ein Objekt eine kinetische Energie besitzen, welche größer oder gleich der potentiellen Energie des Gravitationsfeldes ist. Für die Fluchtgeschwindigkeit v₂ gilt also:

$\frac{1}{2} m \cdot v_2^2 = \frac{G \cdot M \cdot m}{r}$

$v_2 = \sqrt{\frac {2 \cdot G \cdot M}{r}}$

wobei G die Gravitationskonstante, M die Masse des Planeten und r der Planetenradius bzw. der Abstand vom Mittelpunkt des Planeten sind. Werden für M die Erdmasse und für r der Erdradius eingesetzt, ergibt sich für die Erde eine Fluchtgeschwindigkeit v₂ von 11,2 km/s^[2].

Die Fluchtgeschwindigkeit liegt immer um den Faktor 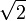$\sqrt{2}$ über der Kreisbahngeschwindigkeit des Planeten.

Fluchtgeschwindigkeit in der Raumfahrt

Interplanetare Raumsonden befinden sich häufig zuerst auf einer Erdumlaufbahn, bevor die Triebwerke erneut gezündet werden und den Flugkörper auf die Fluchtgeschwindigkeit beschleunigen. Hierbei leistet die Umlaufgeschwindigkeit bereits einen großen Beitrag zur notwendigen Endgeschwindigkeit.

Für Flugbahnen zum Mond muss die Fluchtgeschwindigkeit nicht vollständig erreicht werden, vielmehr muss die maximale Entfernung des Flugkörpers zur Erde der Distanz Erde–Mond entsprechen. Die tatsächliche Flugbahn ist durch den Einfluss des Mondes (eingeschränktes Dreikörperproblem) nicht algebraisch berechenbar.

Spezialfall Schwarzes Loch

Einen Spezialfall stellt ein Schwarzes Loch dar. Hier ist die Fluchtgeschwindigkeit innerhalb des sogenannten Ereignishorizontes größer als die Lichtgeschwindigkeit c, welche nicht überschritten werden kann. Somit kann nichts, was hinter den Ereignishorizont gerät, dem Schwarzen Loch entkommen. Aufgrund relativistischer Effekte gilt dies sogar für beschleunigte Objekte.

Beispiele

Einige Fluchtgeschwindigkeiten:

Himmels- körper	Fluchtgeschwindigkeit am Äquator
	in m/s	in km/s	in km/h
Merkur	4.300	4,3	15.480
Venus	10.200	10,2	36.720
Erde	11.200	11,2	40.320
Mond	2.300	2,3	8.280
Mars	5.000	5,0	18.000
Jupiter	59.600	59,6	214.560
Saturn	35.500	35,5	127.800
Uranus	21.300	21,3	76.680
Neptun	23.300	23,3	83.880
Pluto	1.100	1,1	3.960
Sonne	617.300	617,3	2.222.280

Dritte kosmische Geschwindigkeit

Wird die Fluchtgeschwindigkeit nicht auf die Erde, sondern auf die Sonne angewandt, spricht man auch von der dritten kosmischen Geschwindigkeit, die notwendig ist, um das Sonnensystem zu verlassen. Hierbei wird für r üblicherweise die Entfernung Erde–Sonne eingesetzt, so dass sich ein Wert von 42,1 km/s ergibt, der für eine ruhende Erde gilt. Da die Umlaufgeschwindigkeit der Erde um die Sonne bereits 29,8 km/s beträgt, ist bei günstiger Abschussrichtung nur eine Geschwindigkeit von 12,3 km/s relativ zur Erde notwendig, um das Sonnensystem zu verlassen.

Vierte kosmische Geschwindigkeit

Die vierte kosmische Geschwindigkeit ist schließlich nötig, um auch die Milchstraße zu verlassen. Aus der Angabe, dass die Sonne für einen Umlauf um das galaktische Zentrum im Abstand von 28.000 Lichtjahren 230 Millionen Jahre benötigt, ergibt sich aus dem dritten keplerschen Gesetz für die innere Masse der Galaxie 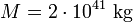$M = 2 \cdot 10^{41} \text{ kg}$^[3], womit die Fluchtgeschwindigkeit von der ruhenden Sonne aus ca. 320 km/s^[4] beträgt. Nutzt man die Umlaufgeschwindigkeit der Sonne um die Galaxis, die bei 220 km/s liegt, reduziert sich die vierte kosmische Geschwindigkeit auf ca. 100 km/s.

Quellen

• Universität München: Kosmische Geschwindigkeiten
• Urbin.de: Welche Rolle spielt die Himmelsmechanik?

1. ↑ Berechnung der ersten kosmischen Geschwindigkeit für die Erde mit dem Google Calculator
2. ↑ Berechnung der zweiten kosmischen Geschwindigkeit für die Erde mit dem Google Calculator
3. ↑ Google Rechner: Masse der Galaxis
4. ↑ Berechnung der vierten kosmischen Geschwindigkeit für die Erde mit dem Google Calculator