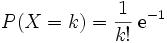Drittelgesetz

Das Gesetz der kleinen Zahlen, Zwei-Drittel-Gesetz oder Gesetz des Drittels ist eine Konsequenz aus der Poisson-Verteilung.

Die Bezeichnung Gesetz der kleinen Zahlen geht auf den russischen Mathematiker Ladislaus von Bortkewitsch (1898) zurück. Obwohl Bortkewitsch dieses Gesetz bei der Untersuchung der Anzahlen der Todesfälle durch Hufschlag in den einzelnen Kavallerie-Einheiten der preußischen Armee fand, wird es fast immer anhand des Roulettespiels dargestellt:

Das Gesetz der kleinen Zahlen beim Roulette

Betrachtet man beim Roulette mehrere Rotationen, d. h. Serien von jeweils 37 einzelnen Spielen (Coups), so stellt man fest, dass im Laufe einer Rotation nur ungefähr zwei Drittel der Nummern getroffen werden, davon etwa die Hälfte sogar mehrfach, während das verbleibende Drittel nicht getroffen wird – daher die von den „Roulette-Wissenschaftlern“ gebrauchten Bezeichnungen Zwei-Drittel-Gesetz oder Gesetz des Drittels.

Im Laufe einer Rotation beim Roulette werden im Mittel

• 36,8% der Nummern, d. h. 13,6 Zahlen nicht getroffen
• 36,8% der Nummern, d. h. 13,6 Zahlen genau einmal getroffen
• 18,4% der Nummern, d. h. 6,8 Zahlen genau zweimal getroffen
• 6,1% der Nummern, d. h. 2,3 Zahlen genau dreimal getroffen
• 1,9% der Nummern, d. h. 0,7 Zahlen viermal oder öfter getroffen.

Nach dem Gesetz der großen Zahlen tritt im langfristigen Mittel jede der 37 Zahlen mit der gleichen relativen Häufigkeit auf, d. h. ist die Anzahl von Coups genügend groß, so entfällt auf jede einzelne Nummer der gleiche Anteil, nämlich 1/37 = 2,7%. Betrachtet man mehrere Rotationen und eine im vorhinein bestimmte Zahl, so wird diese im Mittel in jeder Rotation einmal getroffen.

Dies verleitet viele Spieler zum Fehlschluss, dass in einer Serie von 37 Coups jede einzelne Zahl einmal auftritt. Dies ist aber nicht der Fall; es ist vielmehr extrem unwahrscheinlich, dass jede Nummer genau einmal getroffen wird; die Wahrscheinlichkeit hierfür beträgt nur 1,3·10^-15.

Trotz der Gleichwahrscheinlichkeit aller Zahlen tritt im Falle einer kleinen Anzahl von Spielen keine Gleichverteilung ein, sondern das obige durch die Wahrscheinlichkeiten der Poisson-Verteilung vorgegebene Muster.

Auch mit Hilfe des Zwei-Drittel-Gesetzes lässt sich keine Gewinnstrategie finden (siehe Marsch).

Der allgemeine Fall

Das Gesetz der kleinen Zahlen ist eine einfache Anwendung der Poisson-Verteilung für λ = 1 und gilt natürlich nicht nur für Rotationen beim Roulette, sondern für beliebige Serien von n voneinander unabhängigen Spielen, wovon jedes einzelne n gleichwahrscheinliche Ausgänge nehmen kann. So z. B. wenn n Objekte unter n Empfänger verlost werden und die einzelnen Auslosungen voneinander unabhängig sind.

Das Gesetz der kleinen Zahlen trifft umso genauer zu, je größer die Anzahl n ist. Für 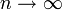$n\to \infty$ strebt der Anteil der Empfänger, die genau k Objekte erhalten, gegen den Wert

$P(X=k) = \frac{1}{k!}\; {\rm e}^{-1}$

Der Anteil der Empfänger, die nichts bekommen, strebt somit gegen 1/e ≈ 36,7879%. Dasselbe gilt für den Anteil derjenigen, die genau einmal bedacht werden.

Beispiel Reiskörner

Zufällig auf dem Boden verstreute Reiskörner

Das Bild rechts zeigt zufällig auf dem Boden verstreut liegende Reiskörner. Bildausschnitt und Rastergröße sind so gewählt, dass im Mittel auf ein Quadrat ein Reiskorn fällt, d. h. es gilt λ = 1.

Das Auszählen der Häufigkeiten bestätigt trotz der kleinen Stichprobengröße von n = 64 die Erwartungswerte:

• 23 Quadrate enthalten kein Reiskorn. Erwartungswert (auf 2 Dezimalen gerundet): 23,54
• 25 Quadrate enthalten genau ein Reiskorn. Erwartungswert: 23,54.
• 12 Quadrate enthalten genau zwei Reiskörner. Erwartungswert: 11,77.
• 2 Quadrate enthalten genau drei Reiskörner. Erwartungswert: 3,92.
• 2 Quadrate enthalten vier oder mehr Reiskörner (1 x 4 bzw. 1 x 5). Erwartungswert: 1,22.

(Die Summe der Erwartungswerte ergibt auf eine Dezimale gerundet: 64,0.)

Siehe auch

• Zufall