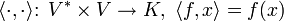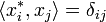- Dualbasis
-
Der (algebraische) Dualraum ist ein Begriff aus dem mathematischen Teilgebiet der linearen Algebra.
Zu einem Vektorraum V über einem Körper K bezeichnet V * den zu V gehörigen Dualraum, das heißt die Menge aller linearen Abbildungen von V nach K. Seine Elemente werden je nach Kontext auch Funktionale, Linearformen oder auch 1-Formen genannt. Insbesondere in der Physik verwendet man gerne die Sprache der Tensoralgebra; dann heißen die Elemente von V kontravariante, die von V * kovariante Vektoren, oder auch Kovektoren.
Durch die nachfolgende Definition der Addition und der skalaren Multiplikation von K auf V * ist V * selbst ein Vektorraum über dem Körper K.
Hierzu definiert man die vektorielle Addition:
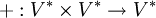 durch
durch 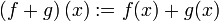 für alle
für alle 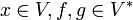
und die skalare Multiplikation:
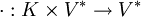 durch
durch 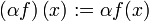 für alle
für alle 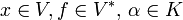
Ist V ein endlich-dimensionaler Vektorraum so ist auch V * endlich-dimensional, und es gilt: dimKV * = dimKV.
Sei
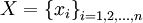 eine endliche Basis von V, dann heißt
eine endliche Basis von V, dann heißt 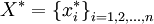 mit
mit-
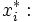
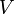

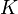 linear und
linear und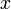
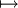
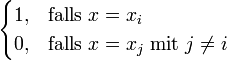
die duale Basis zur Basis X und ist eine Basis des Dualraumes V * .
Ist V ein unendlich-dimensionaler Vektorraum, so lässt sich auf diese Art und Weise i.A. keine duale Basis konstruieren. (Sei
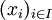 eine Basis des unendlichdimensionalen Vektorraums V. Man betrachte die lineare Abbildung
eine Basis des unendlichdimensionalen Vektorraums V. Man betrachte die lineare Abbildung 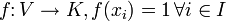 , die in V * liegt, aber keine endliche Linearkombination der
, die in V * liegt, aber keine endliche Linearkombination der 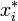 ist. Daher bilden die
ist. Daher bilden die 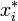 kein Erzeugendensystem von V * .)
kein Erzeugendensystem von V * .)Die Wirkung der Elemente von V * auf V definiert eine Bilinearform:
Damit lässt sich die Wirkung dualer Basisvektoren
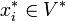 auf Basisvektoren
auf Basisvektoren 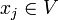 übersichtlich mit dem Kronecker-Delta schreiben:
übersichtlich mit dem Kronecker-Delta schreiben:Inhaltsverzeichnis
Topologischer Dualraum eines normierten Raums
Falls der zugrundeliegende Vektorraum V ein normierter Vektorraum ist, kann man zusätzlich zum algebraischen auch den topologischen Dualraum betrachten. Dieser ist die Menge aller stetigen linearen Funktionale und wird in der Regel mit
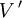 bezeichnet. Die Unterscheidung zwischen algebraischem und topologischem Dualraum ist nur dann wichtig, wenn V ein unendlich-dimensionaler Raum ist. In einem endlich-dimensionalen Raum sind alle linearen Funktionale automatisch stetig, und somit sind der algebraische und der topologische Dualraum identisch. Wenn im Zusammenhang mit Banachräumen von einem Dualraum die Rede ist, ist meistens der topologische Dualraum gemeint. Das Studium der Dualräume von Banachräumen ist eines der Hauptgebiete der Funktionalanalysis.
bezeichnet. Die Unterscheidung zwischen algebraischem und topologischem Dualraum ist nur dann wichtig, wenn V ein unendlich-dimensionaler Raum ist. In einem endlich-dimensionalen Raum sind alle linearen Funktionale automatisch stetig, und somit sind der algebraische und der topologische Dualraum identisch. Wenn im Zusammenhang mit Banachräumen von einem Dualraum die Rede ist, ist meistens der topologische Dualraum gemeint. Das Studium der Dualräume von Banachräumen ist eines der Hauptgebiete der Funktionalanalysis.Der topologische Dualraum ist wieder ein normierter Vektorraum mit der Norm
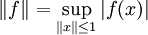 .
.Ist V ein Vektorraum über einem analytisch vollständigen Körper (also z. B.
 oder
oder  ), dann ist der Dualraum immer vollständig, also ein Banachraum.
), dann ist der Dualraum immer vollständig, also ein Banachraum.Besonders einfach ist der (topologische) Dualraum, falls V ein Hilbertraum ist. Nach einem Satz, den M. Fréchet 1907 für separable und F. Riesz 1934 für allgemeine Hilberträume bewiesen hat, sind ein Hilbertraum und sein Dualraum isometrisch isomorph zueinander, siehe Rieszscher Darstellungssatz. Die Vertauschbarkeit von Raum und Dualraum kommt besonders deutlich in der Bra-Ket-Schreibweise von Dirac zum Ausdruck. Diese wird besonders in der Quantenmechanik verwendet, denn die quantenmechanischen Zustände werden durch Vektoren in einem Hilbertraum modelliert.
Da jeder endlich-dimensionale Vektorraum über den reellen oder komplexen Zahlen isomorph zu einem Hilbertraum ist, sind endlich-dimensionale Räume stets selbstdual.
Der starke Dualraum eines lokalkonvexen Raums
Ist E ein lokalkonvexer Raum, so bezeichnet E' wie im Falle der normierten Räume den Raum der stetigen, linearen Funktionale. Die Auszeichnung einer geeigneten Topologie auf dem Dualraum ist aufwändiger. Folgende Definition ist so angelegt, das sich im Spezialfall des normierten Raums die oben beschriebene Normtopologie auf dem Dualraum ergibt:
Ist
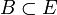 beschränkt, so definiert
beschränkt, so definiert 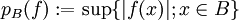 eine Halbnorm auf E'. Die Menge der Halbnormen pB, wobei B die beschränkten Mengen von E durchläuft, definiert die sogenannte starke Topologie auf E'. Man nennt E' mit der starken Topologie den starken Dualraum und bezeichnet ihn manchmal genauer mit Eb', wobei das tiefgestellte b für beschränkt (engl. bounded, frz. borné) steht.
eine Halbnorm auf E'. Die Menge der Halbnormen pB, wobei B die beschränkten Mengen von E durchläuft, definiert die sogenannte starke Topologie auf E'. Man nennt E' mit der starken Topologie den starken Dualraum und bezeichnet ihn manchmal genauer mit Eb', wobei das tiefgestellte b für beschränkt (engl. bounded, frz. borné) steht.Die schwach-*-Topologie ist ebenfalls eine häufig betrachtete Topologie auf E', diese fällt aber im Falle unendlich-dimensionaler normierter Räume nicht mit der oben beschriebenen Normtopologie auf dem Dualraum zusammen. In der Theorie der lokalkonvexen Räume ist daher mit Dualraum in der Regel der starke Dualraum gemeint.
Bidual
Da der Dualraum V' eines Banachraums wieder ein Banachraum ist, kann man den Dualraum des Dualraums, den sogenannten Bidualraum V'' betrachten. Hier ist interessant, dass es eine kanonische Einbettung von V in V'' gibt, die durch
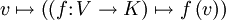 gegeben ist. (Das heißt: jedes Element des ursprünglichen Raumes V ist auf natürliche Weise auch ein Element des Bidualraums). Wenn sich jedes Element des Bidualraums durch ein Element aus V darstellen lässt, genauer wenn die kanonische Einbettung ein Isomorphismus ist, dann heißt der Banachraum reflexiv. Reflexive Räume sind einfacher zu handhaben als nicht reflexive. Sie sind in gewisser Weise den Hilberträumen am ähnlichsten. Ein Beispiel für einen nicht-reflexiven Raum ist der Raum C[0,1] der stetigen Funktionen auf dem Einheitsintervall mit der Maximumsnorm.
gegeben ist. (Das heißt: jedes Element des ursprünglichen Raumes V ist auf natürliche Weise auch ein Element des Bidualraums). Wenn sich jedes Element des Bidualraums durch ein Element aus V darstellen lässt, genauer wenn die kanonische Einbettung ein Isomorphismus ist, dann heißt der Banachraum reflexiv. Reflexive Räume sind einfacher zu handhaben als nicht reflexive. Sie sind in gewisser Weise den Hilberträumen am ähnlichsten. Ein Beispiel für einen nicht-reflexiven Raum ist der Raum C[0,1] der stetigen Funktionen auf dem Einheitsintervall mit der Maximumsnorm.Ein anderes Beispiel für nicht-reflexive Räume sind Banachräume, bei denen die kanonische Einbettung kein Isomorphismus ist, es aber einen anderen Isomorphismus zwischen Raum und Bidualraum gibt. Ein Beispiel dafür sind die sogenannten Jamesräume, nach Robert Clarke James.
Beispiele
In der folgenden Aufstellung wird zu einem Banachraum V der ersten Spalte ein weiterer Banachraum W in der zweiten Spalte angegeben, der im Sinne der in der dritten Spalte angegebenen Dualität isometrisch isomorph zum Dualraum von V ist. Genauer bedeutet dies: Jedes Element aus W definiert durch die Formel der Dualität ein stetiges lineares Funktional auf V. Dadurch erhält man eine Abbildung
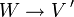 , und diese ist linear, bijektiv und isometrisch.
, und diese ist linear, bijektiv und isometrisch.Banachraum Dualraum Dualität Bemerkung c0 = Raum der Nullfolgen mit der Supremumsnorm 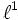 = Raum der absolut summierbaren Folgen mit der Norm
= Raum der absolut summierbaren Folgen mit der Norm 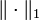
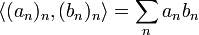
c = Raum der konvergenten Folgen mit der Supremumsnorm 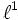 = Raum der absolut summierbaren Folgen mit der Norm
= Raum der absolut summierbaren Folgen mit der Norm 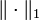
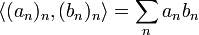
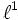 = Raum der absolut summierbaren Folgen mit der Norm
= Raum der absolut summierbaren Folgen mit der Norm 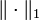
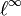 = Raum der beschränkten Folgen mit der Supremumsnorm
= Raum der beschränkten Folgen mit der Supremumsnorm 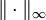
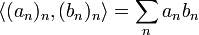
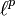 = Raum der in p-ter Potenz absolut summierbaren Folgen mit der Norm
= Raum der in p-ter Potenz absolut summierbaren Folgen mit der Norm 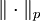
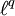 = Raum der in q-ter Potenz absolut summierbaren Folgen mit der Norm
= Raum der in q-ter Potenz absolut summierbaren Folgen mit der Norm 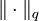
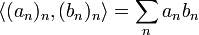
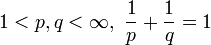
K(H) = Raum der kompakten Operatoren auf dem Hilbertraum H N(H) = Raum der nuklearen Operatoren auf dem Hilbertraum H 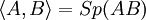
siehe nuklearer Operator N(H) = Raum der nuklearen Operatoren auf dem Hilbertraum H B(H) = Raum der beschränkten Operatoren auf dem Hilbertraum H 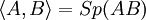
siehe nuklearer Operator N(E) = Raum der nuklearen Operatoren auf E B(E,E'') = Raum der beschränkten Operatoren 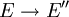
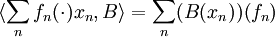
E Banachraum mit Approximationseigenschaft, siehe nuklearer Operator 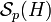 = p-Schatten-Klasse auf dem separablen Hilbertraum H
= p-Schatten-Klasse auf dem separablen Hilbertraum H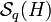 = q-Schatten-Klasse auf dem separablen Hilbertraum H
= q-Schatten-Klasse auf dem separablen Hilbertraum H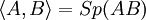
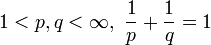
Lp(X,μ) = Raum der in p-ter Potenz integrablen Funktionen mit der Norm 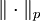
Lq(X,μ) = Raum der in q-ter Potenz integrablen Funktionen mit der Norm 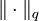
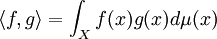
(X,μ) Maßraum, 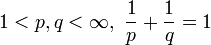 , siehe Lp-Raum
, siehe Lp-RaumL1(X,μ) = Raum der integrablen Funktionen mit der Norm 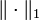
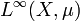 = Raum der wesentlich beschränkten, messbaren Funktionen mit der Norm
= Raum der wesentlich beschränkten, messbaren Funktionen mit der Norm 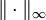
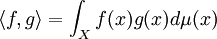
(X,μ) σ-endlicher Maßraum 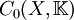 = Raum der stetigen
= Raum der stetigen 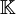 -wertigen Funktionen, die im Unendlichen verschwinden, mit der Supremumsnorm
-wertigen Funktionen, die im Unendlichen verschwinden, mit der Supremumsnorm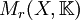 = Raum der regulären Borelmaße mit der totalen Variation als Norm
= Raum der regulären Borelmaße mit der totalen Variation als Norm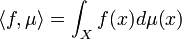
X lokalkompakter Hausdorffraum Siehe auch
Literatur
- Dirk Werner: Funktionalanalysis. Springer Verlag, 2005. ISBN 3-540-43586-7
Wikimedia Foundation.