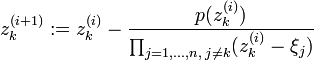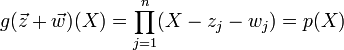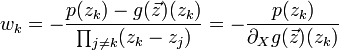Durand-Kerner-Verfahren

Das Weierstraß-(Durand-Kerner)-Verfahren (W-(D-K)-Verfahren) ist ein iteratives Verfahren zur simultanen Bestimmung aller Nullstellen eines univariaten Polynoms. Es ist benannt nach Karl Weierstraß, der es als Teil eines Beweises zum Fundamentalsatz der Algebra zwischen 1859 und 1891 entwickelte, sowie E. Durand und Immo Kerner, die es 1960 bzw. 1966 in einen Computeralgorithmus überführten.

Das Verfahren

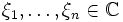Es sei $p(X)=X^n+p_{n-1}X^{n-1}+\dots+p_0$ ein normiertes univariates Polynom mit komplexen Koeffizienten und mit führendem Koeffizienten 1. Dieses hat nach dem Fundamentalsatz der Algebra genau n Nullstellen $\xi_1,\dots,\xi_n\in\mathbb C$ und kann in Linearfaktoren zerlegt werden,

$p(X)=(X-\xi_1)\cdot\ldots\cdot(X-\xi_n)$.

Aus dieser Formel kann jede der Nullstellen formal isoliert werden, es gilt

$\xi_k=X-\frac{p(X)}{\prod_{j=1,\dots,n,\;j\ne k}(X-\xi_j)}$.

Diese Formel kann als triviale Fixpunktiteration verstanden werden, die Iteration

$z_k^{(i+1)}:=z_k^{(i)}-\frac{p(z_k^{(i)})}{\prod_{j=1,\dots,n,\;j\ne k}(z_k^{(i)}-\xi_j)}$

wird offensichtlich nach dem ersten Iterationsschritt in der Nullstelle ξ_k stationär.

Ersetzt man nun in der Iterationsvorschrift die anderen Nullstellen durch gute Näherungen, so bleibt ξ_k ein Fixpunkt und jede Iteration, die in der Nähe dieser Nullstelle startet, konvergiert auch gegen diese. Die Iteration des W-(D-k)-Verfahrens ergibt sich, wenn nun für alle Nullstellen gleichzeitig mittels dieser Iterationsvorschrift Näherungsfolgen bestimmt werden, und die jeweils bestimmte Näherung einer Nullstelle sofort in die Bestimmung der nächsten Näherungen der anderen Nullstellen eingeht.

Am Anfang eines jeden Iterationsschrittes stehen n paarweise verschiedene komplexe Zahlen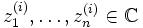 $z_1^{(i)},\dots,z_n^{(i)}\in\mathbb C$. Für den ersten Schritt können diese Zahlen 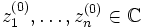$z_1^{(0)},\dots,z_n^{(0)}\in\mathbb C$ zufällig, aber paarweise verschieden gewählt werden, in späteren Schritten stehen diese Zahlen für Approximationen der Nullstellen von p(X).

Dem Tupel 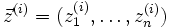$\vec z^{(i)}=(z_1^{(i)},\dots,z_n^{(i)})$ wird das Polynom 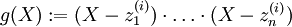$g(X):=(X-z_1^{(i)})\cdot\ldots\cdot(X-z_n^{(i)})$ zugeordnet, das diese komplexen Zahlen als Nullstellen hat. Von diesem Polynom wird die Ableitung g'(X) nach der Unbestimmten X bestimmt. Es gelten

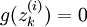$g(z_k^{(i)})=0$ und $g'(z_k^{(i)})=\prod_{j\ne k}(z_k^{(i)}-z_j^{(i)})$.

Aus p(X) und der Ableitung 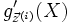$g_{\vec z^{(i)}}'(X)$ werden die Weierstraß-Korrekturen 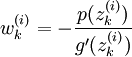$w_k^{(i)}=-\frac{p(z_k^{(i)})}{g'(z_k^{(i)})}$, k=1,...,n bestimmt und das korrigierte Tupel 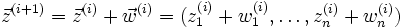$\vec z^{(i+1)}=\vec z^{(i)}+\vec w^{(i)}=(z_1^{(i)}+w_1^{(i)},\dots,z_n^{(i)}+w_n^{(i)})$ als Ergebnis und Eingabe des nächsten Iterationsschrittes erhalten.

Die Iteration kann z. B. abgebrochen werden, wenn die Korrektur eine zuvor festgelegte Rückgabegenauigkeit unterschreitet. (Die Rechengenauigkeit sollte etwas höher als diese Rückgabegenauigkeit sein.)

Beispiel

Zu lösen sei die kubische Gleichung x³ − 3x² + 3x − 5 = 0. Als Starttupel werde (z₁,z₂,z₃) = (a⁰,a¹,a²) mit dem komplexen Parameter 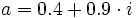$a=0.4+0.9\cdot i$ gewählt. Es ergeben sich die folgenden ersten Iterationsschritte

It.-Nr.	z1	z2	z3
0	+1.0000+0.0000i	+0.4000+0.9000i	-0.6500+0.7200i
1	+1.3608+2.0222i	-0.3658+2.4838i	-2.3858-0.0284i
2	+2.6597+2.7137i	+0.5977+0.8225i	-0.6320-1.6716i
3	+2.2704+0.3880i	+0.1312+1.3128i	+0.2821-1.5015i
4	+2.5428-0.0153i	+0.2044+1.3716i	+0.2056-1.3721i
5	+2.5874+0.0000i	+0.2063+1.3747i	+0.2063-1.3747i
6	+2.5874+0.0000i	+0.2063+1.3747i	+0.2063-1.3747i

In den ersten 4 Iterationen wird das Tripel (z₁,z₂,z₃) scheinbar chaotisch bewegt, ab dem 5 Schritt bleiben zunehmend mehr Dezimalstellen konstant, Iteration 6 bestätigt die Korrektheit von Iteration 5 im Rahmen der angegebenen Genauigkeit. Dieses allgemeine Verhalten ist charakteristisch für diese Methode.

Als Gleichung 3. Grades mit reellen Koeffizienten hat p(X) eine reelle Nullstelle und ein konjugiertes Paar komplexer Nullstellen. Die Näherungen erfüllen dieses Muster. Nach der Satzgruppe von Vieta muss z. B. die Summe aller Nullstellen dem Negativen des Koeffizienten zweithöchsten Grades entsprechen, also 3 sein. Auch dies bestätigt sich in den Näherungen.

Begründung als Newton-Verfahren

Die – wenigstens lokale – Konvergenz der Weierstraß-Iteration ergibt sich aus ihrer Interpretation als mehrdimensionales Newton-Verfahren. Das Gleichungssystem dazu ergibt sich aus dem Vergleich der Koeffizienten gleichen Grades in der angestrebten Identität

$g(\vec z)(X)=\prod_{j=1}^n(X-z_j)=p(X)$.

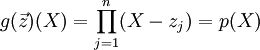Da die Polynome auf beiden Seiten normiert sind (der höchstgradige Koeffizient ist 1), ist die Identitat im Grad n trivial und es ergeben sich n Gleichungen für die n Unbekannten.

Im Allgemeinen ist diese Identität nicht erfüllt. Die Korrektur 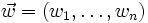$\vec w=(w_1,\dots,w_n)$ in jedem Schritt der Newton-Iteration ergibt sich aus der Forderung, dass die Identität

$g(\vec z+\vec w)(X)=\prod_{j=1}^n(X-z_j-w_j)=p(X)$

in erster Ordnung in 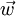$\vec w$ erfüllt sei. Aus der Taylor-Entwicklung erster Ordnung ergibt sich die in 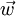$\vec w$ lineare Gleichung

$g(\vec z)(X)-\sum_{k=1}^n w_k\,\prod_{j\ne k}(X-z_j)=p(X)$.

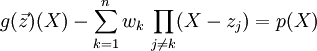Jede einzelne Korrektung w_k kann daraus durch Einsetzen von X = z_k zu

$w_k=-\frac{p(z_k)-g(\vec z)(z_k)}{\prod_{j\ne k}(z_k-z_j)} =-\frac{p(z_k)}{\partial_Xg(\vec z)(z_k)}$

gewonnen werden, was die oben angegebene Weierstraß-Korrektur ergibt.

Ein globaler Konvergenzbeweis für dieses Verfahren wurde schon in (K. Weierstraß 1891) als alternativer Beweis für den Fundamentalsatz der Algebra angegeben.

Fehlerschätzung mittels Gerschgorin-Kreisen

Eine Fehlerabschätzung und eine alternative Herleitung des Verfahrens ist im Artikel zum Satz von Gerschgorin angegeben. Danach sind in jedem Iterationsschritt alle Nullstellen des Polynoms p(X) in der Vereinigung der Kreisscheiben 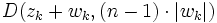$D\big(z_k+w_k, (n-1)\cdot|w_k|\big)$ enthalten. Sind die Kreisscheiben paarweise disjunkt, so enthält jede genau eine Nullstelle. (A. Neumaier 2003) zeigt die gleiche Aussage für die etwas kleineren Kreisscheiben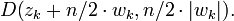 $D\big(z_k+n/2\cdot w_k,n/2\cdot|w_k|\big).$

Literatur

• Karl Weierstraß: Neuer Beweis des Satzes, dass jede ganze rationale Function einer Veränderlichen dargestellt werden kann als ein Product aus linearen Functionen derselben Veränderlichen. In: Sitzungsberichte der königlich preussischen Akademie der Wissenschaften zu Berlin. 1891.
• E. Durand: Equations du type F(x)=0: Racines d'un polynome. In: Masson et al. (Hrsg.): Solutions numeriques des equations algebriques. Vol. 1. 1960,
• Immo O. Kerner, I.: Ein Gesamtschrittverfahren zur Berechnung der Nullstellen von Polynomen. In: Numerische Mathematik. 8, 1966, S. 290-294
• Prešić, Marica: A convergence theorem for a method for simultaneous determination of all zeros of a polynomial. In: Publications de l'institut mathematique (Beograd) (N.S.). 28(42), 1980, S. 158-168
• Petkovic, M.S., Carstensen, C. and Trajkovic, M.: Weierstrass formula and zero-finding methods. In: Numerische Mathematik. 69, 1995, S. 353-372
• Bo Jacoby, Nulpunkter for polynomier, CAE-nyt (a periodical for Dansk CAE Gruppe [Danish CAE Group]), 1988.
• Agnethe Knudsen, Numeriske Metoder (lecture notes), Københavns Teknikum.
• Bo Jacoby, Numerisk løsning af ligninger, Bygningsstatiske meddelelser (Published by Danish Society for Structural Science and Engineering) volume 63 no. 3-4, 1992, pp. 83-105.
• Xavier Gourdon: Combinatoire, Algorithmique et Geometrie des Polynomes. Ecole Polytechnique, Paris 1996 (Postscript ; Stand: 15.10.2006). 
• Victor Pan (May 2002): Univariate Polynomial Root-Finding with Lower Computational Precision and Higher Convergence Rates. Tech-Report, City University of New York
• Arnold Neumaier: Enclosing clusters of zeros of polynomials. In: Journal of Computational and Applied Mathematics. 156, 2003

Weblinks

• Jan Verschelde, The method of Weierstrass (also known as the Durand-Kerner method), 2003.
• Roots Extraction from Polynomials : The Durand-Kerner Method - contains a Java applet demonstration