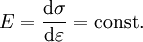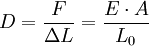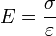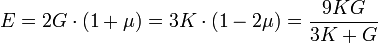E-Modul

Der Elastizitätsmodul (auch: Zugmodul, Elastizitätskoeffizient oder Youngscher Modul, benannt nach dem englischen Arzt und Physiker Thomas Young) ist ein Materialkennwert aus der Werkstofftechnik, der den Zusammenhang zwischen Spannung und Dehnung bei der Verformung eines festen Körpers bei linear elastischem Verhalten beschreibt.

Der Elastizitätsmodul wird mit E-Modul oder als Formelzeichen mit E abgekürzt und hat die Einheit einer mechanischen Spannung.

Der Plural von "der Elastizitätsmodul" lautet korrekt "die Elastizitätsmoduln". Oft wird aber auch die Form "die Module" (korrekt für die Mehrzahl von "das Modul" = zusammengesteckte Bauteile, z. B. die Solarmodule), "die Moduli" (aus dem Lateinischen eingedeutscht) oder "die Modulen" verwendet.

Der Betrag des Elastizitätsmoduls ist umso größer, je mehr Widerstand ein Material seiner Verformung entgegensetzt. Ein Bauteil aus einem Material mit hohem Elastizitätsmodul (z. B. Stahl) ist also steif, ein Bauteil aus einem Material mit niedrigem Elastizitätsmodul (z. B. Gummi) ist nachgiebig.

Der Elastizitätsmodul ist die Proportionalitätskonstante im Hookeschen Gesetz. Bei kristallinen Materialien ist der Elastizitätsmodul grundsätzlich richtungsabhängig. Sobald ein Werkstoff eine kristallographische Textur hat, ist der Elastizitätsmodul also anisotrop. Bei Materialien mit Orientierungen oder anisotropen Füllstoffen wie Fasern wird meist auch ein richtungsabhängiger Elastizitätsmodul gefunden.

Definition

Schematisches Spannungs-Dehnungs-Diagramm: für kleine Dehnungen linear, Hookesche Gerade mit Steigung E

Der Elastizitätsmodul ist als Steigung des Graphen im Spannungs-Dehnungs-Diagramm bei einachsiger Belastung innerhalb des linearen Elastizitätsbereichs definiert. Dieser lineare Bereich wird auch als Hookesche Gerade bezeichnet.

$E=\frac{\mathrm{d}\sigma}{\mathrm{d}\varepsilon}=\mathrm{const.}$

Dabei bezeichnet σ die mechanische Spannung (Normalspannung, nicht Schubspannung) und ε die Dehnung. Die Dehnung ist das Verhältnis von Längenänderung zur ursprünglichen Länge. Die Einheit des Elastizitätsmoduls ist die einer Spannung:

E in 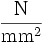$\mathrm{\frac{N}{mm^2}}$, in SI-Einheiten: E in 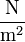$\mathrm{\frac{N}{m^2}}$ (Pascal)

Der Elastizitätsmodul wird als Materialkonstante bezeichnet, da mit ihm und den Querkontraktionszahlen das Elastizitätsgesetz aufgestellt wird. Der Elastizitätsmodul ist aber nicht bezüglich aller physikalischen Größen konstant. Er hängt von verschiedenen Umgebungsbedingungen wie z. B. Temperatur, Feuchte oder der Verformungsgeschwindigkeit ab.

Anwendung

Bei ideal linear elastischem Werkstoffgesetz (Proportionalitätsbereich im Spannungs-Dehnungs-Diagramm) ergibt sich die Federkonstante D eines geraden Stabes aus seiner Querschnittsfläche A, seiner Länge L₀ und seinem Elastizitätsmodul E.

$D=\frac{F}{\Delta L}=\frac{E \cdot A}{L_0}$

Mit den Ausdrücken 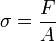$\sigma=\frac{F}{A}$ für die Spannung und 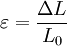$\varepsilon=\frac{\Delta L}{L_0}$ für die Dehnung erhält man aus obiger Gleichung das Hookesche Gesetz für den 1-achsigen Spannungszustand

$\sigma=E \cdot \varepsilon$

und daraus den E-Modul

$E=\frac{\sigma}{\varepsilon}$

Typische Zahlenwerte

Hinweise zur Einheitenumrechnung:

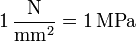• $1\,\frac{\mathrm{N}}{\mathrm{mm}^2}= 1\,\mathrm{MPa}$ (Ein Newton pro Quadratmillimeter ist ein Mega-Pascal)

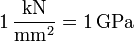• $1\,\frac{\mathrm{kN}}{\mathrm{mm}^2}= 1\,\mathrm{GPa}$ (Ein Kilo-Newton pro Quadratmillimeter ist ein Giga-Pascal)

Metallische Werkstoffe bei 20 °C		Nichtmetallische Werkstoffe bei 20 °C
Material	E-Modul in kN/mm2	Material	E-Modul in kN/mm2
Ferritischer Stahl	210	CFK parallel zur Faser	150
Austenitischer Stahl / martensitischer Stahl	195	Glas	50 bis 90
Sphäroguss	170 bis 185	Glasfaser	55 bis 87
Grauguss	90 bis 155	Beton	22 bis 45
Messing	78 bis 123	Knochen	18 bis 21
Kupfer	120	Holz parallel zur Faser	7 bis 20
Titan	105	CFK quer zur Faser	13
Aluminium	70	Epoxid	~2,5
Magnesium	42	Polyamid	2-4
Blei	16	Polyester	1-5
Invar	130 bis 150	Polypropylen	1-2
Nickel	200	Holz quer zur Faser	0,23 bis 1,33
Wolfram	411	Silikonkautschuk	0,01 bis 0,1

Bei flächigen Bauteilen wird mit Flüssen an Stelle von Spannungen gerechnet 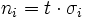$n_i=t\cdot\sigma_i$. Daher setzt man hier einen dickenbezogenen Elastizitätsmodul ein, was einer Steifigkeit entspricht. Diese Größe hat die Einheit $\mathrm{\frac{N}{mm}}$.

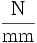Beziehungen elastischer Konstanten

Neben dem Elastizitätsmodul wird auch der Schubmodul, auch Scher- oder G-Modul genannt, verwendet, der in Torsion gemessen wird und je nach Querkontraktionszahl das 0,33- bis 0,5-fache des Elastizitätsmoduls beträgt. Bei steifen Materialien wird meistens der Elastizitätsmodul gemessen, bei weichen (Gele, Polymer-Schmelzen) der Schubmodul, da sich der Elastizitätsmodul bei solchen Systemen meist nicht mehr gut messen lässt, weil sich die Probe unter ihrem eigenen Gewicht verformt, das sog. Sagging.

Es gilt für ein linear-elastisches, isotropes Material folgender Zusammenhang zwischen dem Schubmodul G, dem Kompressionsmodul K und der Poissonzahl μ:

$E = 2G \cdot (1+\mu) = 3K\cdot(1-2\mu) = \frac {9KG} {3K+G}$

Häufige Missverständnisse

„Bezug E-Modul zu anderen Materialkonstanten?“

Häufig wird der Elastizitätsmodul mit anderen Materialkennwerten in Verbindung gebracht. Dies ist jedoch nicht einfach:

• Der E-Modul hat keinen strengen Bezug zur Härte des Materials
• Der E-Modul hat keinen strengen Bezug zur Streckgrenze R_e des Materials
• Der E-Modul hat keinen strengen Bezug zur Zugfestigkeit R_m des Materials

Ein einfacher Baustahl hat (fast) den gleichen E-Modul wie ein hochlegierter hochfester rostfreier Edelstahl.

Es gibt aber einen generellen Trend:

• Der E-Modul eines Metalles steigt mit seiner Schmelztemperatur.

Wolfram hat einen höheren E-Modul als Eisen, als Kupfer, als Aluminium, als Blei.

Außerdem gilt:

• Der E-Modul von kubisch raumzentrierten Metallen ist (bei vergleichbarer Schmelztemperatur) höher als der von kubisch flächenzentrierten.

Der Grund für die Zusammenhänge ist, dass sowohl der E-Modul als auch die Schmelztemperatur der Metalle von der Kraft-Abstands-Kurve der Atome abhängig sind.

„Spannungsreduktion durch besseres Material?“

Bei der Dimensionierung von Bauteilen herrscht oft die Meinung, dass bei einem „besseren“ Material die Spannungen kleiner werden müssten. Die Spannungen hängen aber nur von der Last und der Geometrie ab (Kraft pro Fläche), und nicht vom Material.

In Fällen von "statischer Unbestimmtheit" (z. B. Durchlaufträger, Bewegungen schwimmender Körper im Wellengang oder im Tidenhub, behinderte Wärmeausdehnung) sind die Kräfte und Spannungen abhängig von der Steifigkeit des statischen Systems. In solchen Fällen können Werkstoffe mit niedrigerem Elastizitätsmodul dazu führen, dass Bauteilspannungen reduziert werden.

„E-Modul = Steifigkeit“

Die Steifigkeit eines Bauteils hängt ab vom verwendeten Material und der Verarbeitung, aber auch von der Geometrie des Bauteils. Beim Zugstab ist die Steifigkeit das Produkt aus E-Modul und Querschnittsfläche geteilt durch die Länge, beim Biegebalken hängt die Steifigkeit vom E-Modul, dem Flächenträgheitsmoment und der Länge des Balkens ab. Bei Seilen ist die Steifigkeit außer vom Material sehr stark von der Flechtart abhängig.
Für komplexe Geometrien lässt sich kein einfacher Ausdruck für die „Steifigkeit“ formulieren. Mit Hilfe der Finite-Elemente-Methode lassen sich diese mittels einzelner Elemente nachbilden und mit einer hierfür aufgestellten Gesamtsteifigkeitsmatrix lösen.

„sigma = E * epsilon“

Die Beziehung 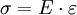$\sigma = E \cdot \varepsilon$ gilt nur für den einachsigen Zug. Im allgemeinen 2D- oder 3D-Spannungszustand muss das Hookesche Gesetz in seiner allgemeinen Form angewandt werden – hier kommen mehrere Spannungen in jeden Dehnungsterm, und mehrere Dehnungen in jeden Spannungsterm, z. B. $\varepsilon_x = \frac 1 E \cdot [\sigma_x - \mu \cdot ( \sigma_y + \sigma_z)]$. Hier bezeichnet μ die Poissonzahl.

Eine Bestimmung der Dehnung, z. B. mittels Dehnungsmessstreifen oder Speckle-Interferometrie ist also noch keine Bestimmung der Spannungen im Bauteil.

Siehe auch

• Elastizitätsgesetz
• Kriechmodul

Weblinks

• Elastizitätsmoduln gängiger Werkstoffe