Effizienter Algorithmus

Die Effizienz eines Algorithmus ist seine Sparsamkeit bezüglich der Ressourcen, Zeit und Speicherplatz, die er zur Lösung eines festgelegten Problems beansprucht. Mit steigender Effizienz sinkt die Komplexität eines Algorithmus. Jedoch sind effiziente Algorithmen meist schwerer zu verstehen, da sie oft auf ausgeklügelten Ideen beruhen. Effiziente Algorithmen sind schnell in der Lösung des entsprechenden Problems.

Bewertung der Effizienz

Laufzeit- und Speichereffizienz sind nicht alleine eine Eigenschaft des Algorithmus. Die Effizienz wird auch durch die konkrete Implementation in der jeweiligen Programmiersprache, die zugrundeliegende Hardware sowie die Eingabedaten beeinflusst. Deshalb führt man für die Effizienzbewertung unabhängige Faktoren an:

• Laufzeit eines Algorithmus auf Basis der benötigten Rechenschritte
• Speicherbedarf durch Variablen

Ob ein Algorithmus nun als effizient gelten kann oder nicht, hängt vor allem von der Perspektive ab, aus der man den Algorithmus analysiert und was man über die Komplexität des vom Algorithmus behandelten Problems weiß.

Man unterscheidet bei der Effizienz zwischen:

• Worst-Case - das schlechtestmögliche Verhalten
• Average-Case - das durchschnittliche Verhalten
• Best-Case - das bestmögliche Verhalten

Da die Zahl der benötigten Takte für elementare Operationen zwischen verschiedenen Rechnerarchitekturen schwankt, sich in der Regel aber nur um einen konstanten Faktor unterscheidet und ferner der Laufzeit- und Platzbedarf für kleine Eingaben in der Regel unerheblich ist, nutzt man die Landau-Notation. Dadurch ist das Laufzeitverhalten und der Platzbedarf unter Vernachlässigung eines konstanten Vorfaktors für große Eingabegrößen darstellbar, was jedoch über eine Praxistauglichkeit des Algorithmus noch nichts aussagt, da in der Praxis meistens mit relativ kleinen Eingabegrößen gearbeitet wird, die Landau-Notation jedoch sehr große Eingabegrößen betrachtet.

Der Begriff effizienter Algorithmus wird in der theoretischen Informatik recht schwammig benutzt. Meist meint man damit einen Algorithmus, dessen Laufzeit polynomial in der Größe der Eingabe ist, aber auch solche Algorithmen können praktisch unbrauchbar sein, wenn beispielsweise der feste Exponent k des zugehörigen Polynoms n^k zu groß ist. Es gibt sogar Linearzeit-Algorithmen, die praktisch unbrauchbar sind, weil der konstante Vorfaktor c in der Darstellung 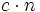$c\cdot n$ zu groß ist. Somit kann es sein, dass obwohl ein Algorithmus A in der Theorie deutlich effizienter ist als ein Algorithmus B, in der Praxis immer nur Algorithmus B verwendet wird, weil die zu bearbeitenden Eingabegrößen nicht groß genug sind, damit Algorithmus A seine Vorteile ausspielen kann.

Optimierung der Effizienz

Die Menge belegten Speichers einer Datenstruktur muss immer im Verhältnis zur Häufigkeit ihres Auftretens zur Laufzeit eines Programms bewertet werden. Der Aufwand einer Optimierung ist häufig nur dann sinnvoll, wenn viele Objekte des betrachteten Typs im Hauptspeicher angelegt bzw. dauerhaft gespeichert werden. In diesem Fall kann durch Reduzierung des Speicherverbrauchs eine Senkung der Kosten einerseits und eine Erhöhung des Systemdurchsatzes andererseits erreicht werden.

Eine Reduzierung des Speicherverbrauchs von Objekten kann eine Verschlechterung der Ausführungsdauer bestimmter Zugriffe auf die zugrundeliegende Datenstruktur haben, nämlich dann, wenn Teilinformationen zusammengefasst werden, um in Basistypen kompakt gespeichert zu werden. Die Effizienz der eingeführten Kodierungsoperationen spielt hierbei eine Rolle. Die relative Häufigkeit bestimmter Zugriffe in einem typischen Programmlauf muss beachtet werden, um in der Summe optimal zu sein. Die Operationen auf Daten werden in zwei Kategorien eingeteilt: Lesen und Schreiben. Diese entsprechen dem Dekodieren und Kodieren der Teilinformationen und müssen deshalb getrennt betrachtet werden. Ein zusätzlicher Aspekt spielt durch das Modell des abstrakten Datentyps hinein: die interne Repräsentation kann gegebenenfalls ohne Umwandlung in die Komponenten verarbeitet werden.

Ziel ist, eine ausgewogene Lösung zu finden, die Vorteile auf einer Seite nicht mit Effizienzeinbußen auf der anderen Seite bezahlt. Aufwand und Komplexität müssen durch den erzielten Gewinn gerechtfertigt sein. Im Zweifelsfall ist die klare Implementierung der trickreichen vorzuziehen. Das heißt, nicht nur unmittelbarer Resourcenbedarf des einzelnen Algorithmus zur Laufzeit wird betrachtet, sondern abhängig von den Anforderungen die Effizienz des gesamten Systems.

Ein weiteres Ziel ist die Vermeidung von Redundanz bei der Speicherung von Objektzuständen. Es ist auch zu beachten, dass Redundanz die Wartungsfreundlichkeit vermindert. Allerdings kann gerade gezielt eingesetzte Redundanz bei bestimmten Anwendungen die Zugriffsgeschwindigkeit auf Daten deutlich erhöhen.