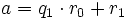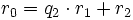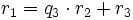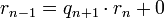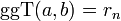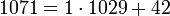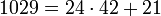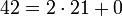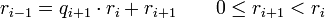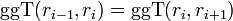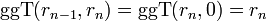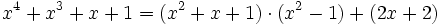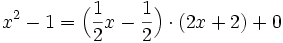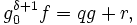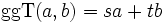Euklidscher Algorithmus

Der euklidische Algorithmus ist ein Algorithmus aus dem mathematischen Teilgebiet der Zahlentheorie. Mit ihm lässt sich der größte gemeinsame Teiler zweier natürlicher Zahlen berechnen. Das Verfahren ist nach dem griechischen Mathematiker Euklid benannt, der es in seinem Werk „Die Elemente“ beschrieben hat.

Der größte gemeinsame Teiler zweier Zahlen kann auch aus ihren Primfaktorzerlegungen ermittelt werden. Ist aber von keiner der beiden Zahlen die Primfaktorzerlegung bekannt, so ist der euklidische Algorithmus das schnellste Verfahren zur Berechnung des größten gemeinsamen Teilers.

Der euklidische Algorithmus lässt sich nicht nur auf natürliche Zahlen anwenden. Vielmehr kann damit der größte gemeinsame Teiler von zwei Elementen eines jeden euklidischen Rings berechnet werden. Dazu zählen beispielsweise Polynome über einem Körper.

Historisches

Der euklidische Algorithmus ist der älteste bekannte nicht-triviale Algorithmus. Das Verfahren wurde von Euklid um 300 v. Chr. in seinem Werk „Die Elemente“ (Buch VII, Proposition 1 und 2) beschrieben. Er nannte es antepheiresis (Wechselwegnahme) und formulierte es als geometrisches Problem: Er suchte ein gemeinsames „Maß“ zweier Strecken. Das Verfahren wurde jedoch wahrscheinlich nicht von Euklid erfunden, sondern war schon bis zu 200 Jahre früher bekannt. Es war mit annähernder Sicherheit Eudoxos von Knidos (um 375 v. Chr.) bekannt und auch Aristoteles (um 330 v. Chr.) wies auf dieses Verfahren in seinem Werk „Topik“ (158b, 29-35) hin.^[1]

Der klassische Algorithmus

Wenn CD aber AB nicht misst, und man nimmt bei AB, CD abwechselnd immer das kleinere vom größeren weg, dann muss (schließlich) eine Zahl übrig bleiben, die die vorangehende misst.

(Aus Euklid, Die Elemente, Herausgegeben von Clemens Thaer, Wissenschaftliche Buchgesellschaft Darmstadt, VII Buch, §2)

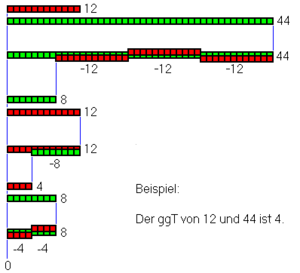
Euklid berechnete den größten gemeinsamen Teiler, indem er nach einem gemeinsamen „Maß“ für die Längen zweier Linien suchte. Dazu zog er wiederholt die kleinere der beiden Längen von der größeren ab.

Ist die Differenz von a und b sehr groß, sind unter Umständen viele Subtraktionsschritte notwendig.
Hippasos von Metapont benutzte schon vor Euklid diese so genannte Wechselwegnahme geometrisch für den Beweis der Inkommensurabilität bei gewissen regelmäßigen n-Ecken: Im Quadrat oder im regelmäßigen Fünfeck etwa gibt es keinen gemeinsamen Teiler (Maß) einer Seite mit der Diagonalen.

Heutzutage wird in der Regel der weiter unten beschriebene Divisions-Algorithmus verwendet, bei dem die Schritte 2 und 3 dadurch ersetzt werden, dass man, an Stelle der Differenz von m und n, für r den Rest bei der Division von m durch n nimmt. Ein weiterer Vorteil dieser Variante ist, dass man sie auf beliebige euklidische Ringe (zum Beispiel Polynomringe, siehe Ringtheorie) übertragen kann, in denen der klassische Algorithmus nicht funktioniert.

Beschreibung durch Pseudocode

Der klassische Algorithmus hier in Pseudocode dargestellt:

EUCLID_OLD(a,b)
1  wenn a = 0
2      dann return b
3  sonst solange b ≠ 0
4      wenn a > b
5          dann a $\leftarrow$ a - b
6          sonst b $\leftarrow$ b - a
7  return a

Dieser Algorithmus kann auch in einer rekursiven Version angegeben werden:

EUCLID_OLD_RECURSIVE(a,b)
1  wenn b = 0
2      dann return a
3      sonst wenn a = 0
4         dann return b
5         sonst wenn a > b
6            dann return EUCLID_OLD_RECURSIVE(a - b, b)
7            sonst return EUCLID_OLD_RECURSIVE(a, b - a)

Moderner Euklidischer Algorithmus

Heutzutage ersetzt man die im klassischen Algorithmus auftretenden wiederholten Subtraktionen eines Wertes jeweils durch eine einzige Division mit Rest. Der moderne euklidische Algorithmus führt nun in jedem Schritt solch eine Division mit Rest aus. Er beginnt mit den beiden Zahlen a und b = r₀ deren größter gemeinsamer Teiler bestimmt werden soll.

$a = q_1 \cdot r_0 + r_1$

In jedem weiteren Schritt wird mit dem Divisor und dem Rest des vorhergehenden Schritts eine erneute Division mit Rest durchgeführt. Und zwar solange bis eine Division aufgeht, das heißt der Rest Null ist.

$r_0 = q_2 \cdot r_1 + r_2$

$r_1 = q_3 \cdot r_2 + r_3$

$\vdots$

$r_{n-1} = q_{n+1} \cdot r_n + 0$

Der Divisor r_n der letzten Division ist dann der größte gemeinsame Teiler.

$\operatorname{ggT}(a,b) = r_n$

Da sich die Zahlen in jedem Schritt mindestens halbieren, ist das Verfahren auch bei großen Zahlen extrem schnell.

Beispiel

Der größte gemeinsame Teiler von 1071 und 1029 wird mit dem Euklidischen Algorithmus wie folgt berechnet:

$1071 = 1 \cdot 1029 + 42$

$1029 = 24 \cdot 42 + 21$

$42 = 2 \cdot 21 + 0$

Der größte gemeinsame Teiler von 1071 und 1029 ist somit 21.

Beschreibung durch Pseudocode

Im Folgenden wird der moderne Euklidische Algorithmus sowohl in einer rekursiven, als auch einer iterativen Variante beschrieben. Dabei sind a und b jeweils die beiden Zahlen deren größter gemeinsamer Teiler berechnet werden soll.

Rekursive Variante

EUCLID(a,b)
1  wenn b = 0
2      dann return a
3      sonst return EUCLID(b, a mod b)

Iterative Variante

EUCLID(a,b)
1  solange b ≠ 0
2      h $\leftarrow$ a mod b
3      a $\leftarrow$ b
4      b $\leftarrow$ h
5  return a

Korrektheit des Algorithmus

In jedem Schritt des Algorithmus wird eine Division mit Rest ausgeführt.

$r_{i - 1} = q_{i + 1} \cdot r_i + r_{i + 1} \qquad 0 \le r_{i + 1} < r_i$

Die Division mit Rest hat die Eigenschaft, dass

$\operatorname{ggT}(r_{i - 1}, r_i) = \operatorname{ggT}(r_i, r_{i + 1})$

gilt.

Im letzten Schritt des Algorithmus

$r_{n - 1} = q_{n + 1} \cdot r_n + 0$

ist r_{n + 1} = 0 und es gilt deshalb

$\operatorname{ggT}(r_{n - 1}, r_n) = \operatorname{ggT}(r_n, 0) = r_n$

Da im ersten Schritt r_{i − 1} = a und r_i = b war, ist

$\operatorname{ggT}(a, b) = r_n$

Laufzeitanalyse

Mit dem euklidischen Algorithmus kann man den ggT mit verhältnismäßig geringem Aufwand (im Vergleich zur Berechnung der Primfaktorzerlegung der Zahlen a und b) berechnen. Bei der Laufzeitanalyse stellt sich heraus, dass der schlimmste Eingabefall zwei aufeinander folgende Fibonacci-Zahlen sind. Bei aufeinander folgenden Fibonacci-Zahlen ergibt sich als Rest immer die nächst kleinere Fibonacci-Zahl. Die Anzahl der benötigten Divisionen beträgt im schlimmsten Fall Θ(log(ab)), wobei log(ab) proportional zur Anzahl der Ziffern in der Eingabe ist (siehe Landau-Symbole).

Da die für die Division zweier Zahlen benötigte Zeit wiederum von der Anzahl der Ziffern der Zahlen abhängt, ergibt sich eine tatsächliche Laufzeit von O(ab•log(ab)) bei naiver Division. Durch die vollständige Überführung der eigentlichen Berechnung in den Frequenzbereich mittels einer speziellen schnellen Fourier-Transformation wie sie im Schönhage-Strassen-Algorithmus Verwendung findet, schneller Reziprokwertberechnung mit dem Newton-Verfahren (im Frequenzbereich) für die Division und anschließender Rücktransformation mittels inverser schneller Fourier-Transformation kommt man so zu einer theoretischen Untergrenze von O(n•log(n)²), wobei n die maximale Anzahl an Ziffern von a und b ist.

Euklidischer Algorithmus und Kettenbruchzerlegung

Die Quotienten, die im euklidischen Algorithmus vorkommen, sind genau die Zahlen, die in der Kettenbruchzerlegung von 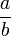$\frac{a}{b}$ vorkommen. Hier für das obige Beispiel mit hervorgehobenen Ziffern:

1071	= 1	× 1029	+ 42
1029	= 24	× 42	+ 21
42	= 2	× 21	+ 0

Hieraus lässt sich der Kettenbruch entwickeln:

$\frac{1071}{1029} = \mathbf{1}+ \frac{42}{1029} = \mathbf{1}+ \frac{1}{\frac{1029}{42}} = \mathbf{1}+ \frac{1}{\mathbf{24}+ \frac{21}{42}} = \mathbf{1}+ \frac{1}{\mathbf{24}+ \frac{1}{\mathbf{2}}} = [1; 24, 2]$.

Dieses Verfahren lässt sich auch für jede beliebige reelle Zahl r anwenden. Ist r nicht rational, so endet der Algorithmus einfach nie. Die so gewonnene Folge an Quotienten stellt dann die unendliche Kettenbruchzerlegung von r dar.

Euklidischer Algorithmus für Polynome

Polynome in einer Variable über einem Körper bilden einen euklidischen Ring. Die Polynomdivision ist für diese Polynome also eine Division mit Rest und der euklidische Algorithmus kann genauso wie bei den ganzen Zahlen durchgeführt werden. Die Berechnung des größten gemeinsamen Teilers der Polynome f = x⁴ + x³ + x + 1 und g = x² − 1 gestaltet sich beispielsweise folgendermaßen:

$x^4 + x^3 + x + 1 = (x^2 + x + 1) \cdot (x^2 - 1) + (2x + 2)$

$x^2 - 1 = \Big(\frac12x - \frac12\Big) \cdot (2x + 2) + 0$

Damit ist 2x + 2 der größte gemeinsame Teiler von f und g.

Polynome mit Koeffizienten aus einem faktoriellen Ring

Wir halten einen faktoriellen Ring (d. h. einen Ring mit bis auf Einheiten eindeutiger Primfaktorzerlegung) R fest und betrachten Polynome aus dem Polynomring R[x], also Polynome in einer Variablen x mit Koeffizienten aus R. Im Spezialfall R = k[y], wobei k ein Körper sei, erhalten wir so den Ring k[x,y] der Polynome in zwei Variablen über k.

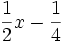In R[x] ist Division mit Rest nicht mehr allgemein durchführbar. Seien z. B. f = x² + 1 und g = 2x + 1 in $\mathbb{Z}[x]$. Polynomdivision in $\mathbb{Q}[x]$ liefert den Quotienten $\frac{1}{2}x-\frac{1}{4}$, der nicht in $\mathbb{Z}[x]$ liegt. Wir können allerdings eine Pseudodivision wie folgt definieren: Seien f und g Polynome aus R[x] mit Grad d_f bzw. d_g, sei g₀ der Leitkoeffizient des Polynoms g, und δ: = d_f − d_g. Dann gibt es Polynome $q,r \in R[x]$, so dass

$g_0^{\delta + 1}f = qg + r,$

wobei wieder r von geringerem Grad ist als g. Durch wiederholte Durchführung der Pseudodivision lässt sich der ggT von f und g bestimmen, allerdings ist das Verfahren in der Praxis ineffizient, da die Faktoren 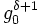$g_0^{\delta+1}$ die Koeffizienten der Zwischenergebnisse exponentiell anwachsen lassen. Um das zu vermeiden kann nach jedem Schritt der Inhalt des Rests r entfernt werden, was allerdings wiederum ggT-Berechnungen in R erfordert. Effizienter lässt sich der ggT mit dem Subresultantenverfahren berechnen.

Varianten

Von Josef Stein stammt der nach ihm benannte steinsche Algorithmus, der ohne die aufwändigen Divisionen auskommt. Er verwendet nur noch Divisionen durch Zwei, die von einem Rechner sehr schnell durchzuführen sind. Aus diesem Grund wird dieser Algorithmus auch binärer euklidischer Algorithmus genannt.

Merkt man sich beim euklidischen Algorithmus die Quotienten q_i der Zwischenschritte, dann lässt sich damit eine Darstellung

$\operatorname{ggT}(a,b) = sa + tb$

mit ganzen Zahlen s und t finden. Dies nennt man den erweiterten euklidischen Algorithmus. Damit lassen sich die Inversen in Restklassenringen berechnen.

Eine andere Erweiterung ist der Algorithmus, der hinter dem Quadratischen Reziprozitätsgesetz steckt. Mit diesem lässt sich das Jacobi-Symbol effizient berechnen.

Quellen

1. ↑ Donald E. Knuth: The Art of Computer Programming. Volume 2: Seminumerical Algorithms. 3. Auflage. Addison-Wesley Professional, 1997, ISBN 0-201-89684-2, S. 334–337