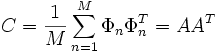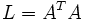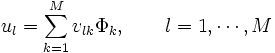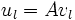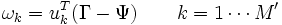Eigenface

Eigengesichter (engl. auch Eigenfaces genannt) ist ein Verfahren zur Gesichtserkennung das auf der Hauptkomponentenanalyse basiert. Entwickelt wurde das Verfahren von Matthew Turk und Alex Pentland.

Geschichte des Verfahrens

Die Eigengesichter basieren auf einem Verfahren von Sirovich und Kirby, mit dem effizient Gesichter komprimiert und wiederhergestellt werden können. Das geschieht mit Hilfe einiger Hauptkomponenten aus der Hauptkomponentenanalyse.

Beschreibung des Verfahrens

Trainingsbilder der Gesichter 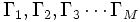$\Gamma_1, \Gamma_2, \Gamma_3 \cdots \Gamma_M$ werden in lexikografischer Reihenfolge eingelesen und in Vektoren gespeichert.

Eigengesichter-Beispiele

Aus dem Trainingsset wird ein Durchschnittsgesicht 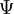$\Psi \!$ gebildet:

$\Psi = \frac{1}{M} \sum_{n=1}^M \Gamma_n$.

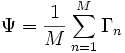Von jedem 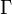$\Gamma \!$ wird ein Differenzgesicht 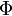$\Phi \!$ gebildet:

$\Phi_i = \Gamma_i - \Psi \!$.

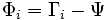Mit Hilfe der Differenzbilder 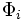$\Phi_i \!$ wird eine Kovarianzmatrix C erstellt:

$C = \frac{1}{M} \sum_{n=1}^M \Phi_n \Phi_n^T = AA^T$

wobei $A = [\Phi_1 \Phi_2 \cdots \Phi_M]$ ist. Die Eigenvektoren der Matrix C sind die Hauptkomponenten, die wegen ihres gesichtsähnlichen Aussehens von Turk und Pentland als Eigengesichter benannt wurden. Das Berechnen der Eigenvektoren aus C ist jedoch in dieser Form für Desktop Computer wegen des sehr großen Speicherbedarfs unmöglich. Dazu gibt es einen anderen effizienteren Weg, da es nur M − 1 wichtige Eigenvektoren gibt. Dazu wird die neue Matrix L berechnet:

$L = A^TA \!$

Die Eigenvektoren v_l von L können ohne Probleme berechnet werden, da L viel kleinere Dimensionen hat. Weiterhin muss folgendes gemacht werden:

$u_l = \sum_{k=1}^M v_{lk} \Phi_k, \qquad l = 1,\cdots,M$

oder anders

$u_l = A v_l \!$

Die somit erhaltenen Vektoren u_l sind die Eigenvektoren von C, wobei uns nur die M' u's mit den höchsten Eigenwerten interessieren. Die u's müssen orthonormal sein, d. h. sie müssen noch normalisiert werden.

Anwendung

Mit Hilfe der ermittelten Eigengesichter u_l können Bilder in den Gesichtsraum projiziert werden (das Bild wird in seine Eigengesicht-Komponenten zerlegt).

$\omega_k = u_k^T (\Gamma - \Psi) \qquad k = 1 \cdots M'$

Der so erhaltene Vektor $\Omega^T = [\omega_1,\cdots,\omega_{M'}]$ kann von einem Mustererkennungs-Algorithmus für eine Gesichtswiedererkennung benutzt werden.

Literatur

• Turk, M., and Pentland, A., "Eigenfaces for Recognition", Journal of Cognitive Neuroscience, Vol. 3, No. 1, pp. 71-86, Winter 1991 (PDF 10,2 MB).
• L. Sirovich and M. Kirby (1987), Low-Dimensional procedure for the characterization of human faces. Journal of the Optical Society of America A, 4(3), 519-524.
• M. Kirby and L. Sirovich. Application of the karhunen-loeve procedure for the characterization of human faces., IEEE Transactions on Pattern Analysis and Machine Intelligence, 12(1):103--108, Jan. 1990.

Weblinks

• http://www.face-rec.org