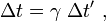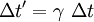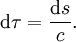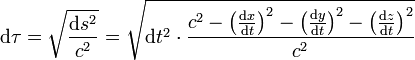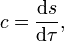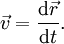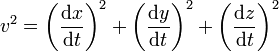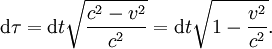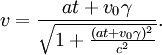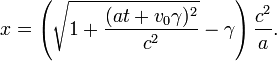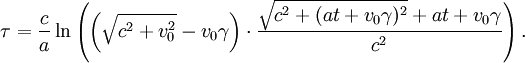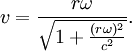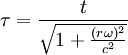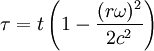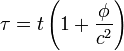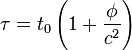Eigenzeit

Bei der Zeitdilatation (aus lat.: dilatare "ausbreiten", "aufschieben") handelt es sich um ein Phänomen der Relativitätstheorie. Befindet sich ein Beobachter im Zustand der gleichförmigen Bewegung bzw. ruht er in einem Inertialsystem, geht nach der speziellen Relativitätstheorie jede relativ zu ihm bewegte Uhr aus seiner Sicht langsamer. Diesem Phänomen unterliegen allerdings nicht nur Uhren, sondern jeder beliebige Vorgang und damit die Zeit im bewegten System selbst. Dabei ist die Zeitdilatation umso stärker, je größer die Relativgeschwindigkeit der Uhr ist, woraus folgt, dass sie nicht im alltäglichen Leben, sondern erst bei Geschwindigkeiten beobachtbar ist, die im Vergleich zur Lichtgeschwindigkeit nicht vernachlässigbar klein sind. Die Tatsache, dass für alle Beobachter die Zeit des jeweils anderen langsamer verstreicht, stellt jedoch keinen Widerspruch dar, wie eine nähere Betrachtung der Relativität der Gleichzeitigkeit aufzeigt (näheres siehe im Artikel spezielle Relativitätstheorie und Minkowski-Diagramm).

Ein solcher Effekt wurde zuerst von Joseph Larmor (1897) und Hendrik Antoon Lorentz (1899) im Rahmen einer inzwischen überholten Äthertheorie abgeleitet. Albert Einstein (1905) gelang es jedoch im Rahmen der speziellen Relativitätstheorie zu zeigen, dass der veränderte Uhrengang nicht mit einer Beeinflussung durch einen Äther, sondern mit einer radikalen Neuinterpretation der Konzepte von Raum und Zeit zusammenhängt (näheres siehe im Artikel Geschichte der speziellen Relativitätstheorie).

Bei der gravitativen Zeitdilatation handelt es sich um ein Phänomen der allgemeinen Relativitätstheorie. Mit der gravitativen Zeitdilatation bezeichnet man den Effekt, dass eine Uhr, und auch jeder physikalische Prozess, in einem Gravitationsfeld langsamer geht als außerhalb desselben. So läuft die Zeit auf der Erdoberfläche relativ um 6,95317 · 10^-10 s langsamer ab als im fernen Weltraum. Genauer gesagt mißt jeder gegenüber dem Gravitationsfeld ruhende Beobachter eine längere bzw. kürzere Ablaufzeit von Vorgängen, die in identischer Weise im bzw. außerhalb des Gravitationsfelds ausgelöst wurden (wie z.B. eine Oszillation des elektrischen Feldstärkevektors eines Lichtstrahls, welche als Zeitbasis verwendet werden kann). Anders als bei der Zeitdilatation durch Bewegung ist die gravitative Zeitdilatation nicht gegenseitig: Während der im Gravitationsfeld weiter oben befindliche Beobachter die Zeit des weiter unten befindlichen Beobachters langsamer ablaufen sieht, sieht der untere Beobachter die Zeit des oberen Beobachters entsprechend schneller ablaufen. Die gravitative Zeitdilatation wurde 1960 im Pound-Rebka-Experiment von Robert Pound und Glen Rebka nachgewiesen.

Zeitdilatation durch relative Bewegung

Bei konstanter Geschwindigkeit

Die Zeitdilatation in einem Inertialsystem, welches sich relativ zu einem anderen Inertialsystem mit einer konstanten Geschwindigkeit v bewegt, ist

$\Delta t = \gamma \ \Delta t'\ ,$

wobei Δt die Zeitdifferenz im ruhenden und Δt' die Zeitdifferenz im bewegten Inertialsystem sind. Der Beobachter beider Inertialsysteme befindet sich hier im ruhenden Inertialsystem.

Wenn sich der Beobachter beider Inertialsysteme im bewegten Inertialsystem befinden würde, dann wäre

$\Delta t' = \gamma \ \Delta t\$

Dabei ist 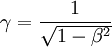$\gamma = \frac{1}{\sqrt{1 - \beta^2}}$ mit β = v / c der Lorentzfaktor.

Lichtuhr

Lichtuhr, links ruhend, rechts mit 25% der Lichtgeschwindigkeit bewegt

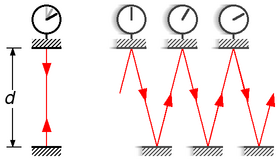
Für eine einfache Erklärung dieses Faktors kann das Konzept der Lichtuhr herangezogen werden. Eine Lichtuhr besteht aus zwei Spiegeln im Abstand d, die einen kurzen Lichtblitz hin und her reflektieren − wobei dieses Gedankenexperiment erstmals 1909 von Gilbert Newton Lewis und Richard C. Tolman besprochen wurde.^[1]

Wenn eine Lichtuhr A gegeben ist, wird aus Sicht eines mit ihr mitbewegten Beobachters ein Blitz für den einfachen Weg zwischen den Spiegeln die Zeit t = d / c benötigen. An einem der beiden Spiegel wird jedes Auftreffen des Lichtblitzes registriert und dabei jedes Mal die Lichtuhr um eine Zeiteinheit weitergestellt, die der Gesamtlaufzeit des Lichtblitzes 2t entspricht.

Wird nun eine zweite Lichtuhr B senkrecht zur Verbindungslinie der Spiegel mit der Geschwindigkeit v bewegt, so muss das Licht aus Sicht des A-Beobachters zwischen den Spiegeln eine größere Strecke zurücklegen als bei Uhr A. Unter der Annahme der Konstanz der Lichtgeschwindigkeit geht für den A-Beobachter Uhr B daher langsamer als Uhr A. Die Zeit t' = d' / c, die der Lichtblitz für den einfachen Weg d' zwischen den Spiegeln benötigt, ergibt sich über den Satz des Pythagoras

d'² = d² + (vt')².

Durch Einsetzen der Ausdrücke für d und d' und Auflösen nach t' erhält man schließlich

$t' = \frac{t}{\sqrt{1 - \frac{v^2}{c^2}}}$.

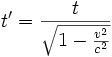Hingegen ein mit Uhr B mitbewegter Beobachter kann gemäß Relativitätsprinzip ebenfalls von sich behaupten, sich in Ruhe zu befinden. Da heißt seine bei ihm befindliche Uhr B wird eine einfache Laufzeit von 2t' für den Lichtblitz anzeigen. Hingegen der Lichtblitz der aus seiner Sicht bewegten Uhr A wird für ihn einen größeren Weg zurücklegen und benötigt folgende Zeit:

$t = \frac{t'}{\sqrt{1 - \frac{v^2}{c^2}}}$.

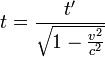Daraus ersieht man die vom Relativitätsprinzip geforderte Symmetrie der Zeitdilatation: Jeder misst, dass die Uhr des jeweils anderen langsamer geht.

Myonen in der Erdatmosphäre

Beim Auftreffen der kosmischen Strahlung auf die Moleküle der oberen Luftschichten entstehen in 9 bis 12 Kilometern Höhe Myonen. Diese bewegen sich in Richtung Erdoberfläche mit nahezu Lichtgeschwindigkeit weiter und können dort detektiert werden. In einem von B. Rossi und D. B. Hall durchgeführten Experiment wurde die Anzahl der Myonen, die in verschiedenen Höhen ankommen, gemessen. Durch eine spezielle Filteranordnung ist es möglich, die Messung auf solche Myonen zu beschränken, die sich mit 99,94 % der Lichtgeschwindigkeit bewegen. Der Vergleich der gemessenen Anzahlen ermöglicht es, die Halbwertszeit der schnell bewegten Myonen zu bestimmen. Diese ist mit 1,3 · 10⁻⁵ s um ein Vielfaches höher als die Halbwertszeit von ruhenden Myonen mit 1,5 · 10⁻⁶ s. Die schnell bewegten Myonen zerfallen also langsamer als ihre unbewegten Gegenstücke.

Reise zu entfernten Sternen

Ein anderes Beispiel wäre die Bewegung eines Raumschiffes, das von der Erde startet, einen entfernten Planeten ansteuert, und wieder zurückkommt. Ein Raumschiff startet von der Erde und fliegt mit der konstanten Beschleunigung von 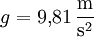$g = 9{,}81\,\frac{\mathrm{m}}{\mathrm{s}^2}$ zu einem 28 Lichtjahre entfernten Stern. Die Beschleunigung von 1g wurde gewählt, da hierdurch irdische Gravitationsverhältnisse an Bord eines Raumschiffes simuliert werden können. Auf halber Strecke ändert das Raumschiff das Vorzeichen der Beschleunigung und verzögert mit 1g. Nach Abschluss einer 6-monatigen Aufenthaltsdauer kehrt das Raumschiff auf gleiche Weise zur Erde zurück. Die vergangenen Zeiten ergeben sich für den Reisenden zu 13 Jahren, 9 Monaten und 16 Tagen (Messung mit an Bord befindlicher Uhr). Auf der Erde sind bei der Rückkehr des Raumschiffes dagegen 60 Jahre, 3 Monate und 5 Stunden vergangen.

Wesentlich extremere Unterschiede bekommt man bei einem Flug zum Andromedanebel, der etwa 2 Millionen Lichtjahre entfernt ist (bei gleichen Beschleunigungs- und Verzögerungsphasen). Für die Erde vergehen etwa 4 Millionen Jahre, während für den Reisenden nur ungefähr 56 Jahre vergangen sind.

Das Raumschiff überschreitet die Lichtgeschwindigkeit nie. Je länger es beschleunigt, desto näher kommt es an die Lichtgeschwindigkeit heran, wird diese jedoch niemals erreichen. Aus Sicht der Erde läuft auf dem Raumschiff die Zeit entsprechend der Zeitdilatation langsamer, der Abstand zwischen Erde und Reiseziel bleibt trivialerweise konstant. Aus Sicht des Raumschiffes läuft die Eigenzeit trivialerweise ganz normal, jedoch verkürzt sich aufgrund der Lorentzkontraktion der Weg zwischen Erde und Reiseziel. Wenn man nun im Raumschiff ist und seine Geschwindigkeit relativ zur Erde unter Berücksichtigung der Lorentzkontraktion bestimmt, dann kommt man auf dasselbe Resultat wie wenn man von der Erde aus die Geschwindigkeit des Raumschiffes bestimmt. Das große Problem an diesem Beispiel ist nur, dass ein Antrieb nicht realisierbar ist, der über so lange Zeit eine so hohe Beschleunigung erreicht.

Näheres hierzu siehe Artikel Zwillingsparadoxon.

Allgemeine Zeitdilatation

Das relativistische Linienelement ds ist definiert durch

ds² = c²dt² − dx² − dy² − dz².

Als Eigenzeitelement gilt der Quotient dieses relativistischen Linienelements oder Abstands ds und der Lichtgeschwindigkeit c

$\mathrm d\tau = \frac{\mathrm d s}{c}.$

Durch Einsetzen und Herausheben von dt² folgt dann

$\mathrm d\tau = \sqrt \frac{\mathrm d s^2}{c^2} = \sqrt {\mathrm d t^2 \cdot \frac{c^2 - \left( \frac{\mathrm d x}{\mathrm d t}\right)^2-\left(\frac{\mathrm \mathrm dy}{\mathrm dt}\right)^2-\left(\frac{\mathrm dz}{\mathrm dt}\right)^2}{c^2} }$

Einerseits ergibt sich mit dem relativistischen Linienelement ds und dem Eigenzeitelement dτ

$c = \frac{\mathrm ds}{\mathrm d\tau},$

anderseits ist eine Geschwindigkeit 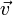$\vec{v}$ allgemein als Ableitung des Ortesvektors 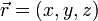$\vec{r}=(x,y,z)$ nach der Zeit t definiert

$\vec{v} = \frac{\mathrm d\vec r}{\mathrm dt}.$

Mit dem Quadrat der Geschwindigkeit

$v^2 = \left(\frac{\mathrm dx}{\mathrm dt}\right)^2+\left(\frac{\mathrm dy}{\mathrm dt}\right)^2+\left(\frac{\mathrm dz}{\mathrm dt}\right)^2$

folgt schließlich für das Element der Eigenzeit

$\mathrm d\tau = \mathrm dt \sqrt { \frac {c^2 - v^2} {c^2} } = \mathrm dt \sqrt{1 - \frac{v^2}{c^2}}.$

Die Eigenzeit τ ist diejenige Zeit, welche im bewegten Bezugssystem vergeht. Da sie langsamer als die Zeit t im Ruhesystem läuft, ist sie stets kleiner als dieselbe - also τ < t. Über das Eigenzeitelement wird integriert, um die Größe zu erhalten

$\tau = \int_0^t \mathrm dt \sqrt{1 - \frac{v^2}{c^2}}$.

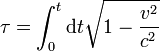Bei konstanter Geschwindigkeit v ist der Wurzelfaktor 1 / γ, und es ergibt sich

$\tau = \frac{t}{\gamma}$.

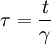In Worten: Wenn im Ruhesystem die Zeit t vergangen ist, ist im bewegten System erst die kleinere Zeit $\frac{t}{\gamma}$ vergangen.

Umgekehrt gilt

t = γτ.

In Worten: Wenn im bewegten System die Zeit τ vergangen ist, so im Ruhesystem die größere Zeit γτ vergangen.

Bewegung mit konstanter Beschleunigung

Die Momentangeschwindigkeit beträgt nach einer in einem ruhenden Inertialsystem vergangenen Zeit t bei der Anfangsgeschwindigkeit v₀ und konstanter Beschleunigung a

$v=\frac{a t + v_0 \gamma}{\sqrt{1+\frac{(a t + v_0 \gamma)^2}{c^2}}}.$

Den zurückgelegten Weg x erhält man durch Integration dieses Ausdrucks über die Zeit

$x = \left( \sqrt{1 + \frac{(a t + v_0 \gamma)^2}{c^2}} - \gamma \right) \frac {c^2}{a}.$

Zur Berechnung der Eigenzeit, also der im bewegten System vergangenen Zeit, muss die Momentangeschwindigkeit in das obige Integral

$\tau = \int_0^t \mathrm dt \sqrt{1 - \frac{v^2}{c^2}}$

eingesetzt werden. Das Ergebnis der Integration ist

$\tau=\frac{c}{a} \ln \left( \left(\sqrt{c^2 + v_0^2} - v_0 \gamma \right) \cdot \frac{\sqrt{c^2 + (a t + v_0 \gamma)^2} + a t + v_0 \gamma}{c^2} \right).$

Zeitdilatation durch Gravitation

Die gravitative Zeitdilatation beschreibt den relativen Zeitablauf von Systemen, die in verschiedenen Entfernungen eines Gravitationszentrums (beispielsweise eines Sterns oder Planeten) relativ zu diesem ruhen. Zu beachten ist, dass die gravitative Zeitdilatation nicht etwa durch eine mechanische Einwirkung auf die Uhren entsteht, sondern eine Eigenschaft der Raumzeit selbst darstellt. Jeder relativ zum Gravitationszentrum ruhende Beobachter misst für identische, jedoch in unterschiedlichen Entfernungen vom Gravitationszentrum ablaufende Vorgänge, unterschiedliche Ablaufzeiten, bezogen auf seine eigene Zeitbasis. Ein Effekt, der auf der gravitativen Zeitdilatation beruht, ist die Gravitationsrotverschiebung.

Beschleunigung und Gravitation: Die rotierende Scheibe

Diese Problemstellung wird auch als Ehrenfestsches Paradoxon bezeichnet.

Nach dem Äquivalenzprinzip der allgemeinen Relativitätstheorie kann man lokal nicht zwischen einem ruhenden System in einem Gravitationsfeld und einem beschleunigten System unterscheiden. Deshalb kann man den Effekt der Gravitations-Zeitdilatation anhand der Zeitdilatation durch Bewegung erläutern.

Betrachten wir eine mit konstanter Winkelgeschwindigkeit ω rotierende Scheibe, so bewegt sich ein Punkt im Abstand r vom Zentrum mit der Geschwindigkeit

$v = \frac{r\omega}{\sqrt{1+\frac{(r\omega)^2}{c^2}}}.$

Dementsprechend wird im Abstand r vom Mittelpunkt der Scheibe die Eigenzeit

$\tau = \frac{t}{\sqrt{1+\frac{(r\omega)^2}{c^2}}}$

auftreten. Für hinreichend kleine Abstände (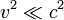$v^2 \ll c^2$) ist dieser Ausdruck näherungsweise

$\tau = t\left(1 - \frac{(r\omega)^2}{2 c^2}\right)$

Ein auf der Scheibe befindliches, mitrotierendes Objekt erfährt nun die Zentrifugalkraft F = mω²r. Aufgrund des Äquivalenzprinzips kann man diese Kraft auch als Gravitationskraft deuten, zu der ein Gravitationspotential

φ = − (rω)² / 2

gehört. Dies ist aber gerade der Term, der bei der Zeitdilatation im Zähler auftritt. Somit ergibt sich für „kleine“ Abstände:

$\tau = t \left(1 + \frac{\phi}{c^2}\right)$

(Hinweis: Das hier angegebene Potential entspricht nicht dem üblichen Zentrifugalpotential, da hier eine Anpassung an die lokale Drehgeschwindigkeit der Scheibe vorgenommen wird, während beim üblichen Zentrifugalpotential stattdessen Drehimpulserhaltung gilt)

Zeitdilatation im Schwerefeld der Erde

In einem schwachen Gravitationsfeld wie dem der Erde kann die Gravitation und somit die Zeitdilatation näherungsweise durch das Newtonsche Gravitationspotential beschrieben werden:

$\tau = t_0 \left(1+\frac{\phi}{c^2}\right)$

Hierbei ist t₀ die Zeit bei Potential φ = 0, und φ das Newtonsche Gravitationspotential (Multiplikation mit der Masse eines Körpers ergibt dessen potentielle Energie an einem bestimmten Ort)

Auf der Erde kann (solange die Höhe klein ist gegen den Erdradius von ca. 6400  Kilometern) das Gravitationspotential durch φ = gh genähert werden. In 300 Kilometern Höhe (das ist eine typische Höhe, in der Space Shuttles fliegen) vergehen somit in jeder „Erdbodensekunde“ 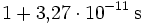$1+3{,}27 \cdot 10^{-11}\,\mathrm{s}$, das ist etwa eine Millisekunde pro Jahr mehr. Das heißt, ein Astronaut, der in 300 Kilometern Höhe über der Erde ruhen würde (zum Beispiel mit Unterstützung eines Raketenantriebs), würde in jedem Jahr etwa eine Millisekunde schneller altern als jemand, der auf der Erde ruht. Zu beachten ist hierbei, dass diese Zahl nicht angibt, wie ein Shuttle-Astronaut altert, da das Shuttle sich zusätzlich bewegt (es kreist um die Erde), was zu einem zusätzlichen Effekt in der Zeitdilatation führt.

Wenn man die durch die Höhe verursachte Verringerung der gravitativen Zeitdilatation relativ zur Erdoberfläche, und die durch die für diese Höhe erforderliche Kreisbahngeschwindigkeit bedingte Zeitdilatation mit einander vergleicht, zeigt sich, dass sich bei einem Bahnradius vom 1,5-fachen des Erdradius, also in einer Flughöhe von einem halben Erdradius, die beiden Effekte genau aufheben, und daher die Zeit auf einer solchen Kreisbahn genau so schnell vergeht, wie auf der Erdoberfläche.

Einzelnachweise

1. ↑ Lewis, Gilbert N. & Tolman, Richard C.: The princicple of relativity, and non-Newtonian mechanics. In: Proceedings of the American Academy of Arts and Sciences. 44, 1909, S. 709-726

Weblinks

• Beispiel-Applet, das demonstriert, dass die Uhr im Raumschiff langsamer geht als die beiden Uhren des Systems, in dem Erde und Pluto unbewegt sind.
• Videos von Vorlesungen der Universität Tübingen über die Zeitdilatation
• Video eines Vortrags aus Physikwiki, der freien Wissensdatenbank Video Zeit, Zeitpfeile und Zeitreisen

Literatur

• Thomas Cremer: Interpretationsprobleme der speziellen Relativitätstheorie. Verlag Harri Deutsch, 1990
• Walter Greiner und Johann Rafelski: Spezielle Relativitätstheorie. Verlag Harri Deutsch, 1989
• Harald Fritzsch: E=mc². Eine Formel verändert die Welt. Piper Verlag, 1990
• Roland Pabisch: Derivation of the time dilatation effect from fundamental properties of photons. Springer, Wien 1999, ISBN 3-211-83153-3