Einsteinsche Summationsregel

Die einsteinsche Summenkonvention ist eine Konvention innerhalb des sogenannten Ricci-Kalküls und stellt eine Indexschreibweise dar. Dieser Kalkül wird in der Tensoranalysis, der Differentialgeometrie und insbesondere in der theoretischen Physik verwendet. Die Summenkonvention wurde 1916 von Albert Einstein eingeführt. Mit ihr werden die Summenzeichen zur Verbesserung der Übersicht einfach weggelassen und stattdessen wird über doppelt auftretende Indizes summiert.

Motivation

In der Matrix- und Tensorrechnung werden oft Summen über Indizes gebildet. Das Matrixprodukt lautet in Komponenten beispielsweise für zwei $n \times n$-Matrizen: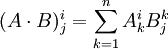

$(A \cdot B)_j^i = \sum_{k=1}^n A_k^i B_j^k$

Hier wird über den Index k von 1 bis n summiert. Treten mehrere Matrixmultiplikationen, Skalarprodukte oder andere Summen in einer Rechnung auf, kann dies schnell unübersichtlich werden. Mit der einsteinschen Summenkonvention lautet die Rechnung von oben dann:

$(A \cdot B)_j^i = A_k^i B_j^k$

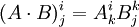
Formale Beschreibung

Über einen Index wird summiert, wenn er in der Indexschreibweise eines Tensors sowohl als kovarianter als auch als kontravarianter Index auftritt. Die Summenkonvention wird ebenfalls angewendet, wenn in einem Produkt bei mehreren Variablen bestimmte Indizes mehrfach vorkommen.

Üblicherweise wird ab drei Indizes in einem Produkt nicht mehr summiert. In der strengen Auslegung der Summenkonvention wird sogar nur summiert, wenn der entsprechende Index bei dem einen Symbol unten und bei dem anderen oben steht. So ist es auch möglich, in einem Produkt zweimal den gleichen Index vorkommen zu lassen, ohne dass summiert wird.

Die Summenkonvention verringert vor allem den Schreibaufwand. Teilweise hilft sie dabei, bestehende Zusammenhänge und Symmetrien hervorzuheben, die in der konventionellen Summenschreibweise nicht so leicht erkennbar sind.

Beispiele

Skalarprodukt

Standardskalarprodukt zweier Vektoren 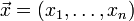$\vec{x} = (x_1, \dots , x_n)$ und $\vec{y} = (y_1, \dots, y_n)$:

$\vec{x} \cdot \vec{y} = x_i y_i$

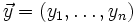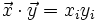
Matrixprodukt

Das Produkt zweier $n \times n$-Matrizen lautet: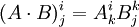

$(A \cdot B)_j^i = A_k^i B_j^k$

Auch wenn beliebig viele Matrizen nacheinander multipliziert werden, lässt sich das Produkt einfach schreiben:

$(A B C \dots X Y Z)_j^i = A^i_a B^a_b C^b_c \dots X^w_x Y^x_y Z^y_j$

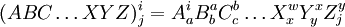
Determinante

Die Determinante einer $3 \times 3$-Matrix lautet:

$\operatorname{det} A = \varepsilon_{ijk}A_1^i A_2^j A_3^k$.

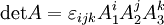Hierbei bezeichnet $\varepsilon$ das Levi-Civita-Symbol.

Literatur

• Albert Einstein, Die Grundlage der allgemeinen Relativitätstheorie, Annalen der Physik, Band 49 (354. Band der ganzen Reihe), S. 770-822, Barth, 1916.

Siehe auch

• Tensor
• Levi-Civita-Symbol