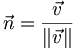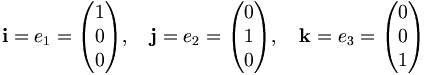- Einsvektor
-
In der linearen Algebra ist ein Einheitsvektor oder normierter Vektor ein Vektor mit der Norm (anschaulich: der Länge) Eins. Einheitsvektoren gibt es also nur in einem normierten Vektorraum.
Inhaltsverzeichnis
Definition
Ein Element v eines normierten Vektorraumes V heißt Einheitsvektor, wenn
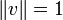 gilt.
gilt.Einordnung
Einen gegebenen, vom Nullvektor verschiedenen Vektor
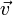 kann man normieren, indem man ihn durch seine Norm (= Betrag) dividiert:
kann man normieren, indem man ihn durch seine Norm (= Betrag) dividiert:Dieser Vektor ist der Einheitsvektor, der in dieselbe Richtung wie
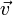 zeigt. Er spielt z. B. eine Rolle beim Gram-Schmidtschen Orthogonalisierungsverfahren oder der Berechnung der Hesseschen Normalform.
zeigt. Er spielt z. B. eine Rolle beim Gram-Schmidtschen Orthogonalisierungsverfahren oder der Berechnung der Hesseschen Normalform.Die Elemente einer Basis (= Basisvektoren) werden oft als Einheitsvektoren gewählt, denn durch die Verwendung von Einheitsvektoren werden viele Rechnungen vereinfacht. Zum Beispiel ist in einem euklidischen Raum das Skalarprodukt zweier Einheitsvektoren gleich dem Kosinus des Winkels zwischen den beiden.
Endlichdimensionaler Fall
In den endlichdimensionalen reellen Vektorräumen
 besteht die am häufigsten bevorzugte Standardbasis aus den kanonischen Einheitsvektoren
besteht die am häufigsten bevorzugte Standardbasis aus den kanonischen Einheitsvektoren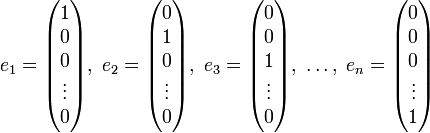 .
.
Fasst man die kanonischen Einheitsvektoren zu einer Matrix zusammen, erhält man eine Einheitsmatrix.
Die Menge der kanonischen Einheitsvektoren des
 bildet bezüglich dem kanonischen Skalarprodukt eine Orthonormalbasis, d. h. je zwei kanonische Einheitsvektoren stehen senkrecht aufeinander (=„ortho“), alle sind normiert (=„normal“) und sie bilden eine Basis.
bildet bezüglich dem kanonischen Skalarprodukt eine Orthonormalbasis, d. h. je zwei kanonische Einheitsvektoren stehen senkrecht aufeinander (=„ortho“), alle sind normiert (=„normal“) und sie bilden eine Basis.Beispiel
Die drei kanonischen Einheitsvektoren des dreidimensionalen Vektorraums
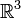 werden in den angewandten Naturwissenschaften manchmal mit
werden in den angewandten Naturwissenschaften manchmal mit 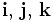 bezeichnet:
bezeichnet:Unendlichdimensionaler Fall
In unendlichdimensionalen unitären Vektorräumen (= VR mit Skalarprodukt) bildet die (unendliche) Menge der kanonischen Einheitsvektoren zwar noch ein Orthonormalsystem, aber nicht notwendig eine (Vektorraum-)Basis. In Hilberträumen gelingt es jedoch durch Zulassung unendlicher Summen, jeden Vektor des Raumes darzustellen, man spricht deshalb weiter von einer Orthonormalbasis.
Siehe auch
Wikimedia Foundation.