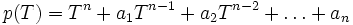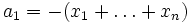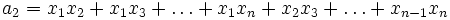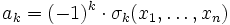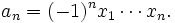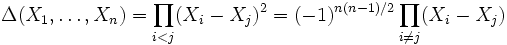- Elementarsymmetrisches Polynom
-
In der Mathematik heißt ein Polynom in mehreren Unbestimmten symmetrisch, wenn man die Unbestimmten untereinander vertauschen kann, ohne das Polynom zu verändern.
Betrachtet man beispielsweise die Polynome p = X + Y − 1 und q = X + Y2, so erhält man durch Vertauschen von X und Y die Polynome
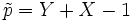 bzw.
bzw. 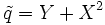 .
.
Da die Addition kommutativ ist, erhält man im Fall von p also dasselbe Polynom, d. h., p ist symmetrisch in X und Y, im Fall von q erhält man ein anderes Polynom, q ist nicht symmetrisch.
Handelt es sich bei dem Polynom um eine Funktion so spricht man auch von symmetrischen Funktionen beziehungsweise von elementarsymmetrischen Funktionen.Inhaltsverzeichnis
Formale Definition
Es seien n > 1 eine natürliche Zahl, A ein Ring. Dann heißt ein Polynom
![p\in A[X_1,\ldots, X_n]](/pictures/dewiki/97/a2bd231ff737c9f0cdf29d6c1080cf35.png) symmetrisch in
symmetrisch in 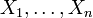 , wenn
, wenn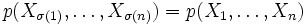 für alle Permutationen
für alle Permutationen 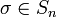
gilt.
Äquivalente Beschreibungen sind:
- Für alle
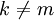 ist
ist
-
- d. h., man kann zwei beliebige Unbestimmte gegeneinander austauschen.
- Es sei
-
- Dann ist p genau dann symmetrisch, wenn
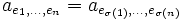 für alle
für alle 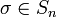
- gilt. Anschaulich bedeutet das, dass der Koeffizient eines Monoms von p nur davon abhängt, welche Exponenten wie oft vorkommen, und nicht, bei welchen Unbestimmten.
- Die symmetrische Gruppe Sn operiert durch
-
- auf dem Polynomring
![A[X_1,\ldots,X_n]](/pictures/dewiki/54/6db64ebd51e05450497af6864094421e.png) . Ein Polynom ist genau dann symmetrisch, wenn es invariant unter dieser Operation ist, d. h., wenn
. Ein Polynom ist genau dann symmetrisch, wenn es invariant unter dieser Operation ist, d. h., wenn
- σp = p für alle
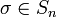
- σp = p für alle
- gilt. Eine mögliche Schreibweise für den Ring der symmetrischen Polynome ist deshalb
Beispiele
- Das Polynom X + Y ist symmetrisch in X und Y, jedoch nicht symmetrisch in X,Y,Z.
Elementarsymmetrische Polynome
Es seien
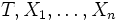 Unbestimmte. Die Koeffizienten von
Unbestimmte. Die Koeffizienten vonals Polynom in T sind symmetrisch in
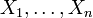 ; sie heißen elementarsymmetrische Polynome. Sie sind explizit angebbar als
; sie heißen elementarsymmetrische Polynome. Sie sind explizit angebbar alsDabei kann man σk auch schreiben als
Eigenschaften
- Die zentrale Aussage über elementarsymmetrische Polynome ist: Jedes symmetrische Polynom lässt sich auf eindeutige Weise als Polynom in den elementarsymmetrischen Polynomen schreiben.
In Formeln:
- Es seien A ein Integritätsbereich,
-
- ein Polynom mit Koeffizienten in A und
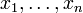 die (mit Vielfachheit gezählten) Nullstellen von p in einem algebraischen Abschluss des Quotientenkörpers von A. Dann gilt nach dem Wurzelsatz von Vieta:
die (mit Vielfachheit gezählten) Nullstellen von p in einem algebraischen Abschluss des Quotientenkörpers von A. Dann gilt nach dem Wurzelsatz von Vieta:
Beispiele
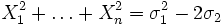
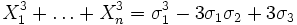 , allgemein sind die Potenzsummen mit den elementarsymmetrischen Polynomen durch die Newton-Identitäten verbunden.
, allgemein sind die Potenzsummen mit den elementarsymmetrischen Polynomen durch die Newton-Identitäten verbunden.- Das Polynom
-
- ist symmetrisch in
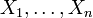 , also kann man es als Polynom in den elementarsymmetrischen Polynomen schreiben. Ist nun
, also kann man es als Polynom in den elementarsymmetrischen Polynomen schreiben. Ist nun
- ein Polynom mit Nullstellen
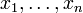 wie oben und setzt man diese in Δ ein, so entsprechen die elementarsymmetrischen Ausdrücke bis auf die Vorzeichen den Koeffizienten ai, d. h.,
wie oben und setzt man diese in Δ ein, so entsprechen die elementarsymmetrischen Ausdrücke bis auf die Vorzeichen den Koeffizienten ai, d. h., 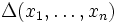 ist ein nur von n abhängendes Polynom in den Koeffizienten
ist ein nur von n abhängendes Polynom in den Koeffizienten 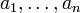 . Bis auf Definitionsvarianten beim Vorzeichen ist dieses Polynom die Diskriminante von p.
. Bis auf Definitionsvarianten beim Vorzeichen ist dieses Polynom die Diskriminante von p.
Wikimedia Foundation.

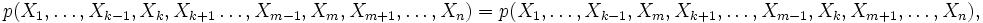
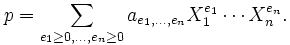
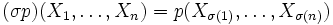
![A[X_1,\ldots,X_n]^{S_n}.](/pictures/dewiki/56/8d3809fba2f4e3a158dbe79b7e3d7617.png)
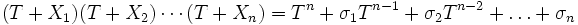
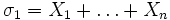
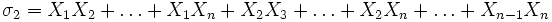
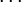
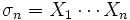
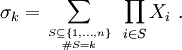
![A[X_1,\ldots,X_n]^{S_n}=A[\sigma_1,\ldots,\sigma_n].](/pictures/dewiki/50/2d01ee62e4146e2e6e07a3c7848e87c2.png)