Elferprobe

Die Neuner- und Elferprobe sind Verfahren zum Nachweis einer fehlerhaften Addition, Subtraktion oder Multiplikation. Der Vorteil dieser Proben liegt darin, dass sich die Richtigkeit des Ergebnisses einer langwierigen Rechnung anhand leichterer alternativer Rechenwege auf Glaubwürdigkeit prüfen lässt.

Umgangssprachlich wird der Begriff Neunerprobe auch allgemein für eine überschlägige Prüfung von Ergebnissen verwendet.

Vorgehensweise

Zunächst wird der jeweilige Rest für die einzelnen Operanden ermittelt.

Der Neunerrest ergibt sich aus der iterativen Quersumme einer Zahl

z.B. für 5387:

5 + 3 + 8 + 7 = 23 und 2 + 3 = 5. Fertig.

Der Elferrest ergibt sich aus der iterativen alternierenden Quersumme einer Zahl

z.B. für 5919:

9 - 1 + 9 - 5 = 12 und 2 - 1 = 1. Fertig.

Dann führt man dieselbe Rechnung mit den Resten an Stelle der ursprünglichen Operanden aus.

Im letzten Schritt prüft man, ob der Rest des ursprünglichen Ergebnisses mit dem Rest des Ergebnisses der Stellvertreterrechnung übereinstimmt. Ist dies nicht der Fall, hat man einen Fehler in der Rechnung aufgedeckt. Stimmen die beiden Ergebnisse jedoch überein, ist das Ergebnis in 8 von 9 Fällen (Neunertest) bzw. in 10 von 11 Fällen (Elfertest) richtig. Das geprüfte Ergebnis kann dann nur genau um Vielfache von 9 (bzw. 11) vom tatsächlichen Ergebnis abweichen. Führt man beide Tests erfolgreich durch, ist das Ergebnis in 98 von 99 Fällen richtig. Das geprüfte Ergebnis kann dann nur genau um Vielfache von 99 vom tatsächlichen Ergebnis abweichen.

Das Verfahren lässt sich gleichermaßen auf Addition, Subtraktionen und Multiplikationen anwenden, wobei eventuell auftretende negative Neunerreste (bzw. Elferreste) in positive überführt werden müssen, indem man 9 (bzw. 11) addiert.

Rechenbeispiele

Addition

Rechnung	Neunerprobe	Elferprobe
573 +492 +145 1210	Rest Probe 6 6 6 +6 1 +1 4 13≡4 4 = 4	Rest Probe 1 1 8 +8 2 +2 0 11≡0 0 = 0

Subtraktion

(mit Zahlendreher)

Rechnung	Neunerprobe	Elferprobe
573 −492 81	Rest Probe 6 6 6 −6 0 0 0 = 0	Rest Probe 1 1 8 -8 7 −7≡4 7 ≠ 4

Hinweis: Die Elferprobe gibt hier einen Fehler aus, weil die Quersumme der Zahl 81 falsch berechnet wurde. Bei der Quersumme für die Elferprobe ist es wichtig, diese von der Einerstelle aus beginnend zu bilden. Die richtige Quersumme wäre also: 81 -> 1 - 8 = -7 ≡ +4. Damit führt auch die Elferprobe nicht mehr zu einem Widerspruch.

Multiplikation

Rechnung	Neunerprobe	Elferprobe
573 ×492 281916	Rest Probe 6 6 6 ×6 9 36≡9 9 = 9	Rest Probe 1 1 8 ×8 8 8 8 = 8

Herkunft

Das Verfahren ist - wohl durch arabische Vermittlung - bereits seit dem 12. Jahrhundert in Europa bekannt.

Im al-Khwarizmis "Algorismus" (9. Jh.) wird die Neunerprobe, aber ohne Verwendung der Quersummen, zum ersten Mal für die Verdopplung und Multiplikation besprochen. Die Faktoren bzw. das Produkt werden durch 9 dividiert und der Rest wird aufgeschrieben. Die so ermittelten Reste entsprechen den Neunerresten der Faktoren bzw. des Produkts.

Einschränkung

Mit der Neunerprobe kann man nicht, wie vielfach angenommen, die Richtigkeit, sondern nur die Fehlerhaftigkeit einer Rechnung nachweisen. Während das Misslingen der Neunerprobe klar ausschließt, dass man korrekt gerechnet hat, lässt ihr Gelingen die Korrektheit der Ergebnisses lediglich wahrscheinlicher werden: das Ergebnis könnte beispielsweise durch Vertauschen der Ziffern trotz erfolgreicher Neunerprobe falsch sein. Zur weiteren Prüfung kann die Elferprobe angeschlossen werden, deren zusätzliches Gelingen die Wahrscheinlichkeit der Korrektheit auf 98:99 erhöht.

Hinweis: Es sollte bedacht werden, dass in der Neunerprobe selbst natürlich Rechenfehler stecken können; besonders wenn man sie selten anwendet (im Computerzeitalter anzunehmen), kann man sich bereits beim Ermitteln der Neunerreste im Kopf leicht vertun.

Andere Basen

Die besondere Bedeutung der Neuner- und Elferprobe im Dezimalsystem ergibt sich daraus, dass sich der Neunerrest einfach als Quersumme und der Elferrest als alternierende Quersumme berechnen lässt. Wegen

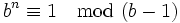$b^n\equiv 1 \mod (b-1)$ und

$b^n\equiv (-1)^n \mod (b+1)$

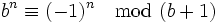
lassen sich in einem Stellenwertsystem zur Basis b die Proben mit den Zahlen b-1 und b+1 besonders einfach durchführen. Beispielsweise ergibt im Hexadezimalsystem die Quersumme den 15er-Rest und die alternierende Quersumme den 17er-Rest. Die 15er und die 17er-Probe sehen dann beispielsweise für die Rechnung A1F+C02 folgendermaßen aus:

Rechnung	15er-Probe	17er-Probe
A1F +C02 1621	Rest Probe B B E +E A 25≡A A = A	Rest Probe 7 7 E +E 4 21≡4 4 = 4

Quellen

Mohammed ibn Musa Alchwarizmi's Algorismus : Das frühste Lehrbuch zum Rechnen mit indischen Ziffern : Nach der einzigen (lateinischen) Handschrift (Cambridge Un. Lib. Ms. Ii.6.5.) in Faksimile mit Transkription und Kommentar - Hrsg. von Kurt Vogel - Otto Zeller: Aalen, 1963.