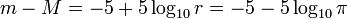Entfernungsmodul

Die absolute Helligkeit ist eine Hilfsgröße in der Astronomie, um die tatsächlichen Helligkeiten, also die Leuchtkräfte, von Himmelsobjekten (meist Sternen) vergleichen zu können.

Von der Erde aus sieht man einen Stern mit seiner scheinbaren Helligkeit, da sie durch seine Entfernung und interstellare Materie beeinflusst wird.

Um die tatsächliche Helligkeit vergleichen zu können, stellt man sich die Sterne in einheitlicher Entfernung vor. Diese beträgt zehn Parsec (32,6 Lichtjahre). Die Helligkeit, die ein Beobachter aus dieser Normdistanz messen würde, nennt man absolute Helligkeit. Bei Sternen, die weniger als zehn Parsec entfernt sind, ist die scheinbare Helligkeit größer als die absolute Helligkeit und umgekehrt. Wie auch bei der scheinbaren Helligkeit bedeutet ein kleinerer Zahlenwert größere Leuchtkraft.

Absolute Helligkeiten werden wie scheinbare Helligkeiten in Magnituden (mag) angegeben. Insbesondere in älteren Werken zur Astronomie findet man häufig die Schreibweise mit einem hochgestellten M über dem Dezimalkomma, beispielsweise 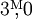$3\stackrel{\text{M}}{,}0$ bei einem Stern der dritten (absoluten) Größenklasse. Die Verwendung des Großbuchstabens verdeutlicht dabei, dass es sich um eine absolute Helligkeit handelt.

Die hellsten Fixsterne erreichen absolute Helligkeiten von etwa −9 mag (über 100.000-fache Leuchtkraft der Sonne), die lichtschwächsten dagegen +17 mag (etwa ein zehntausendstel der Sonnenleuchtkraft).

Bolometrische Helligkeit

Hauptartikel: Bolometrische Helligkeit

Diese gibt die Helligkeit eines Sterns im gesamten elektromagnetischen Spektrum an. Die hierfür erforderliche Korrektur hängt vom Empfindlichkeitsbereich des Messgerätes sowie vom Spektraltyp des betreffenden Objektes ab. Die fotografische Helligkeit der Sonne beträgt 5^M,16, die bolometrische Helligkeit dagegen 4^M,74.

Entfernungsmodul

Die Differenz zwischen scheinbarer Helligkeit m (in der Entfernung r parsec) und absoluter Helligkeit M (in der Entfernung 10 parsec) wird Entfernungsmodul genannt. Gemäß der Festlegung der Helligkeitsstufen gilt: m − M = −2,5 * log (10² / r²). Daraus folgt die Formel für den Entfernungsmodul:

$m - M = -5 + 5 \log_{10} r = -5 -5 \log_{10} \pi\,$

Dabei ist r der Abstand des Sterns in Parsec, π dessen Parallaxe. Mit Hilfe dieser für die Astronomie wichtigen Formel kann für Sterne, deren Leuchtkraft bekannt ist (z. B. Cepheiden oder Supernovae vom Typ Ia), der Abstand berechnet werden. (Auf diese Weise konnte 1923 der Abstand des Andromedanebels ermittelt werden.)

m − M	Entfernung		m − M	Entfernung
	Parsec	Lichtjahre		Parsec	Lichtjahre
− 5	1	3,26	+ 5,5	125,89	410,61
− 4	1,58	5,17	+ 6,0	158,49	516,93
− 3	2,51	8,19	+ 6,5	199,53	650,78
− 2	3,98	12,98	+ 7,0	251,19	819,28
− 1	6,31	20,58	+ 7,5	316,23	1.031,41
0	10	32,62	+ 8,0	398,11	1.298,47
+ 1	15,85	51,69	+ 8,5	501,19	1.634,68
+ 2	25,12	81,93	+ 9,0	630,96	2.057,94
+ 3	39,81	129,85	+ 9,5	794,33	2.590,80
+ 4	63,10	205,79	+ 10	1.000	3.261,62
+ 5	100	326,16	+ 25	1.000.000	3.261.619

Vergleich Scheinbare / Absolute Helligkeit einiger Sterne

Stern	Scheinbare H. (mV)	Absolute H. (MV)	Entfernungsmodul (mV − MV)	Entfernung
Sonne	− 26m,73	+ 4M,84	− 31,57	4,851·10-6 pc
Sirius	− 1m,46	+ 1M,43	− 2,89	2,64 pc
Wega	+ 0m,03	+ 0M,58	− 0,55	7,75 pc
Pollux	+ 1m,15	+ 1M,08	+ 0,07	10,34 pc
Spica	+ 1m,04	− 3M,51	+ 4,55	81,3 pc
Rigel	+ 0m,12	− 6M,78	+ 6,90	240 pc

Objekte im Sonnensystem

Bei Kometen und Asteroiden wird der Begriff Absolute Helligkeit abweichend definiert, da sie nur Licht reflektieren. Hier wird Situation angenommen, dass das Objekt (der Komet oder Asteroid) genau eine astronomische Einheit entfernt von der Sonne steht und von der Sonne aus beobachtet wird. Die Helligkeit, mit der das Objekt dann zu sehen wäre, wird als absolute Helligkeit bezeichnet.

Siehe auch

• Bolometrische Helligkeit
• Cepheiden
• Hertzsprung-Russell-Diagramm