Erneuerungsfolge

Ein Erneuerungsprozess 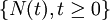$\{N(t), t\ge 0\}$ ist ein Sonderfall eines Zählprozesses, in dem die Zwischenankunftszeiten 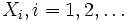$X_i, i=1,2,\ldots$ unabhängige, identisch verteilte, nichtnegative Zufallsvariablen sind. Der Begriff Erneuerung hat seinen Ursprung in industriellen Anwendungen der Wahrscheinlichkeitsrechnung. Typischerweise besitzen Systemkomponenten (z. B. Maschinen, Werkzeuge, Beleuchtungskörper) Lebenszeiten, die den Charakter nichtnegativer Zufallsvariablen haben. Wenn solche Komponenten ausfallen, müssen sie ersetzt werden (erneuert) durch gleichartige Komponenten, um das Funktionieren des Systems zu gewährleisten.

Eigenschaften

N(t) ist definiert als die Anzahl der Erneuerungen bis zum Zeitpunkt t. Dieser stochastischen Prozess wird bestimmt vom Prozess $\{S_n, n=0,1,\ldots\}$:

$S_n=\sum_{i=1}^n X_i,\qquad S_0\equiv 1, \,$

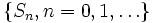dabei bezeichnen die X_i die Zwischenankunftszeiten, z. B. die Lebenszeiten von Komponenten. 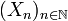$(X_n)_{n \in \mathbb{N}}$ wird auch als Erneuerungsfolge bezeichnet.

Mit anderen Worten: S_n ist der Zeitpunkt der n-ten Erneuerung. Die Äquivalenz der Beschreibung über N(t) und S_n kommt zum Ausdruck in der grundlegenden Beziehung

$\{N(t)\ge n\}\equiv \{S_n\le t\}\quad(\implies\quad P(N(t)\ge n) = P(S_n\le t)) \,$

Ein Erneuerungsprozess ist daher vollständig charakterisiert durch die gemeinsame Verteilung 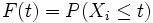$F(t)=P(X_i\le t)$ der Zwischenankunftszeiten X_i. Da S_n Summe unabhängiger Zufallsvariablen ist, ist die Verteilung F_n(t) von S_n die n-fache Faltung der Verteilung F(t), und es gilt:

$\begin{matrix} P(N(t)=n) &=& P(S_n\le t)-P(S_{n+1}\le t)\\ &=& F_n(t)-F_{n+1}(t) \end{matrix}$

Die mittlere Anzahl der Erneuerungen im Zeitintervall (0,t) heißt Erneuerungsfunktion. Diese ist eine Funktion M(t), die mittels der Verteilungen F_n(t) im Prinzip exakt angegeben werden kann:

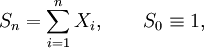
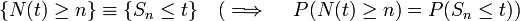
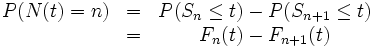
$M(t)=E[N(t)] = \sum_{n=1}^\infty n\left[F_n(t)-F_{n+1}(t)\right]=\sum_{n=1}^\infty F_n(t) \,$