Euklids Primzahlbeweis

Der Satz von Euklid besagt, dass es unendlich viele Primzahlen gibt. Dieser Satz geht auf den griechischen Mathematiker Euklid zurück, der um 300 v. Chr. in Alexandria lebte. In seinem Werk Die Elemente schrieb er: „Es gibt mehr Primzahlen als jede vorgelegte Anzahl von Primzahlen“ (Buch IX, Proposition 20).

Beweis von Euklid

Euklid verwendete einen Widerspruchsbeweis, um die Aussage des Satzes zu beweisen.

Angenommen, es gäbe nur endlich viele Primzahlen 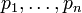$p_1, \ldots, p_n$. Es sei m die kleinste Zahl, die von allen diesen Zahlen geteilt wird. Ist m + 1 eine Primzahl, dann ist sie nach Konstruktion größer als 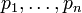$p_1, \ldots, p_n$ und somit eine weitere Primzahl im Widerspruch zur Annahme. Andernfalls sei q ein Primteiler von m + 1. Wäre q eine der Primzahlen 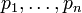$p_1, \ldots, p_n$, so würde q sowohl m als auch m + 1 teilen. Dann muss q aber auch die Differenz, also 1, teilen, was absurd ist. Also ist q eine weitere Primzahl, was wiederum der Annahme widerspricht. Die Annahme, es gäbe nur endlich viele Primzahlen, ist also falsch.

(Euklid führte den Beweis nur mit drei Primzahlen.^[1])

Anwendung

Der Beweis des Satzes von Euklid zeigt eine Möglichkeit auf, wie aus einer oder mehreren vorgegebenen Primzahlen mindestens eine weitere Primzahl berechnet werden kann. Dazu berechnet man das Produkt dieser Primzahlen und addiert 1 zu dem Produkt:

$n = 1 + p_1 \cdot p_2 \cdot ... \cdot p_r = 1 + \prod_{i=1}^r p_i$

Anschließend berechnet man die Primfaktorzerlegung der so gewonnenen Zahl n. Alle Primfaktoren sind dann Primzahlen, die in der ursprünglichen Primzahlmenge nicht enthalten waren.

Es ist eine offene Frage, ob es unter den Zahlen der Form 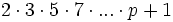$2 \cdot 3 \cdot 5 \cdot 7 \cdot ... \cdot p + 1$ mit p prim, unendlich viele Primzahlen, unendlich viele zusammengesetzte Zahlen oder beides gibt.

Beispiele

Die Zahlen 2, 5 und 11 bilden eine endliche Menge von Primzahlen. Gemäß obiger Formel berechnet sich n zu

$n = 1 + 2 \cdot 5 \cdot 11 = 111 = 3 \cdot 37$.

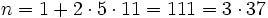Sowohl 3 als auch 37 sind weitere Primzahlen. Anhand der 3 ist zu sehen, dass auch Primzahlen gefunden werden können, die nicht größer als die vorgegebenen Primzahlen sind.

Die Zahlen 2, 3, 5, 7 und 11 bilden eine endliche Menge von Primzahlen. Gemäß obiger Formel berechnet sich n zu

$n = 1 + 2 \cdot 3 \cdot 5 \cdot 7 \cdot 11 = 2311$

2311 ist eine weitere Primzahl. Hier zeigt sich, dass schon das Ergebnis selbst eine Primzahl sein kann.

Die Zahlen 23 und 89 bilden eine endliche Menge von Primzahlen. Gemäß obiger Formel berechnet sich n zu

$n = 1 + 23 \cdot 89 = 2048 = 2^{11}$.

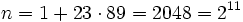2 ist eine weitere Primzahl, die sogar kleiner ist als beide vorgegebenen Primzahlen.

Weitere Beweise

Im Beweisarchiv finden sich weitere Beweise für die Existenz von unendlich vielen Primzahlen.

Einzelnachweise

1. ↑ Die Elemente, Buch IX, Proposition 20