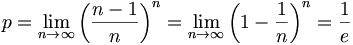- Euler'sche Zahl
-
Die eulersche Zahl e = 2,718281828459... (nach dem Schweizer Mathematiker Leonhard Euler) ist eine irrationale und sogar transzendente reelle Zahl.
Die eulersche Zahl ist die Basis des natürlichen Logarithmus und der (natürlichen) Exponentialfunktion, die aufgrund dieser Beziehung zur Zahl e häufig kurz e-Funktion genannt wird. Sie spielt in der Infinitesimalrechnung (Differential- und Integralrechnung) eine wichtige Rolle.
Inhaltsverzeichnis
Definition
Die Zahl e kann unter anderem durch Grenzwertbildung definiert werden. Die beiden bekanntesten Darstellungen lauten:
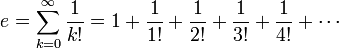 als Reihe.
als Reihe.
Mit k! wird dabei die Fakultät
 bezeichnet. Beide Darstellungen entsprechen dem Funktionswert exp(1) = e1 der Exponentialfunktion (oder „e-Funktion“) an der Stelle 1; die Reihenschreibweise entspricht zudem der Taylorentwicklung der Exponentialfunktion um den Punkt Null an der Stelle 1 ausgewertet.
bezeichnet. Beide Darstellungen entsprechen dem Funktionswert exp(1) = e1 der Exponentialfunktion (oder „e-Funktion“) an der Stelle 1; die Reihenschreibweise entspricht zudem der Taylorentwicklung der Exponentialfunktion um den Punkt Null an der Stelle 1 ausgewertet.Eigenschaften
Die eulersche Zahl e ist eine irrationale (Beweis) und transzendente Zahl (Beweis nach Charles Hermite, 1873). Sie lässt sich also (wie auch die Kreiszahl π nach Ferdinand von Lindemann 1882) weder als Bruch zweier natürlicher Zahlen noch als Lösung einer algebraischen Gleichung endlichen Grades darstellen und besitzt eine unendliche nichtperiodische Dezimalbruchentwicklung.
In der eulerschen Identität
werden fundamentale mathematische Konstanten in Zusammenhang gesetzt: Die ganze Zahl 1, die eulersche Zahl e, die imaginäre Einheit der komplexen Zahlen und die Kreiszahl π.
Herkunft des Symbols e
Der Buchstabe e für diese Zahl wurde zuerst von Euler 1736 in seinem Werk Mechanica benutzt. Es gibt keine Hinweise, dass dies in Anlehnung an seinen Namen geschah, ebenfalls ist unklar, ob er dies in Anlehnung an die Exponentialfunktion oder aus praktischen Erwägungen der Abgrenzung zu den viel benutzten Buchstaben a, b, c oder d machte. Obwohl auch andere Bezeichnungen in Gebrauch waren, etwa c in d'Alemberts Histoire de l'Académie, hat sich e durchgesetzt.
Weitere Darstellungen für die eulersche Zahl
Die eulersche Zahl lässt sich auch durch
oder durch den Quotienten aus Fakultät und Subfakultät beschreiben:
Eher von exotischem Reiz als von praktischer Bedeutung ist die catalansche Darstellung
Die Kettenbruchentwicklung von e weist folgendes Muster auf, welches sich bis ins Unendliche fortsetzt:
Die ersten 200 Nachkommastellen von e
Die Dezimalbruchentwicklung von e mit Nennung der ersten 200 Nachkommastellen lautet:
- e = 2,71828182845904523536028747135266249775724709369995
- 95749669676277240766303535475945713821785251664274
- 27466391932003059921817413596629043572900334295260
- 59563073813232862794349076323382988075319525101901...
Anschauliche Interpretationen der eulerschen Zahl
Zinseszinsrechnung
Das folgende Beispiel macht die Berechnung der eulerschen Zahl nicht nur anschaulicher, sondern es beschreibt auch die Geschichte der Entdeckung der eulerschen Zahl: Ihre ersten Stellen wurden von Jakob Bernoulli bei der Untersuchung der Zinseszinsrechnung gefunden.
Den Grenzwert der ersten Formel kann man folgendermaßen deuten: Jemand zahlt am 1. Januar einen Euro auf der Bank ein. Die Bank garantiert ihm eine momentane Verzinsung zu einem Zinssatz p=100 % pro Jahr. Wie groß ist sein Guthaben am 1. Januar des nächsten Jahres?
Nach der Zinseszinsformel ist das Kapital nach n Verzinsungen Kn = K0(1 + p / 100)n, wobei K0 das Startkapital, p der Zinssatz, und n die Anzahl der Verzinsungen sind.
In diesem Beispiel sind K0 = 1 und p = 100, wenn der Zinszuschlag jährlich erfolgt, oder p = 100 / n, wenn der Zinszuschlag n mal im Jahr erfolgt.
Bei jährlichem Zuschlag wäre
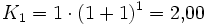 . Bei halbjährlichem Zuschlag hat man p = 100 / 2, also
. Bei halbjährlichem Zuschlag hat man p = 100 / 2, also 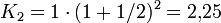 , also schon etwas mehr. Bei täglicher Verzinsung (p = 100 / 365) erhält man
, also schon etwas mehr. Bei täglicher Verzinsung (p = 100 / 365) erhält man 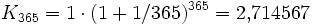 . Wenn man momentan verzinst, wird n unendlich groß, und man bekommt die oben angegebene erste Formel für e.
. Wenn man momentan verzinst, wird n unendlich groß, und man bekommt die oben angegebene erste Formel für e.Wahrscheinlichkeitsrechnung
e ist auch häufig in der Wahrscheinlichkeitstheorie anzutreffen (siehe auch Exponentialfunktion, Stochastik): Angenommen, ein Bäcker gibt für jedes Brötchen eine Rosine in den Teig und knetet gut durch. Nachher enthält statistisch gesehen jedes e-te Brötchen keine Rosine. Die Wahrscheinlichkeit p, dass bei n Brötchen alle n Rosinen in anderen Brötchen sind, ergibt im Grenzwert für
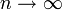 (37%-Regel):
(37%-Regel):Sonstige Eigenschaften
Die zwei Teilkurven der impliziten Funktion xy − yx = 0 schneiden sich im Punkt P(e / e). Mehrdimensionale Verallgemeinerungen dieser Funktion setzen sich im n-dimensionalen Raum aus
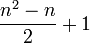 Teilkurven zusammen, die sich alle in einem Punkt schneiden, dessen Koordinaten sämtlich e betragen. Der Beweis hierfür ist nicht leicht zu führen.
Teilkurven zusammen, die sich alle in einem Punkt schneiden, dessen Koordinaten sämtlich e betragen. Der Beweis hierfür ist nicht leicht zu führen.Siehe auch
Weblinks
- Schönhacker: Die Zahl e (Diplomarbeit, PDF, 850 Kb)
- Intuitiv verständliche Verbildlichung von e in einem interaktiven Java-Applet
- Die e-Funktion für Schüler erklärt
- Die Umkehrfunktion der e-Funktion für Schüler erklärt
- e auf eine Million Stellen bei Project Gutenberg (englisch)
- ausführliche Informationen und Angaben zu relevanter Literatur (englisch)
Wikimedia Foundation.

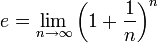 als Grenzwert einer
als Grenzwert einer 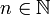 oder
oder 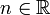 voraussetzt) und
voraussetzt) und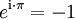
![e = \lim_{n\to\infty} \frac{n}{\sqrt[n]{n!}}](/pictures/dewiki/49/1ece0ee65e250a7a3ec0a38140ef258c.png)
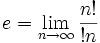
![e=\sqrt[1]{\frac{2}{1}}\cdot\sqrt[2]{\frac{4}{3}}\cdot\sqrt[4]{\frac{6\cdot 8}{5\cdot 7}}\cdot\sqrt[8]{\frac{10\cdot 12\cdot 14\cdot 16}{9\cdot 11\cdot 13\cdot 15}}\cdots](/pictures/dewiki/99/cf562e91091a5e52d0e3d117a573e394.png)
![e = [2; 1, 2, 1, 1, 4, 1, 1, 6, 1, 1, 8, 1, 1, 10, 1,\dots] = 2+\cfrac{1}{1+\cfrac{1}{2+\cfrac{1}{1+\cfrac{1}{1+\cfrac{1}{4+\cfrac{1}{1+\cfrac{1}{1+\cfrac{1}{6+\ldots}}}}}}}}](/pictures/dewiki/54/6fd242f499420fe7b0f7fdc9d363ed5b.png)