- Eulerscher Multiplikator
-
Eine exakte Differentialgleichung (auch vollständig) ist eine gewöhnliche Differentialgleichung der Form
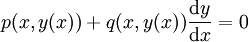 ,
,
bei der es eine stetig differenzierbare Funktion F(x,y) gibt, so dass gilt
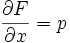 und
und 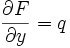 .
.
Eine solche Funktion F heißt dann Potentialfunktion des Vektorfelds (p,q).
Sind p und q stetig partiell differenzierbar und ist der Definitionsbereich von p und q ein einfach zusammenhängendes Gebiet im
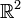 , so gibt es genau dann eine solche Potentialfunktion F, wenn die sogenannte Integrabilitätsbedingung
, so gibt es genau dann eine solche Potentialfunktion F, wenn die sogenannte Integrabilitätsbedingung 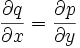 erfüllt ist.
erfüllt ist.Inhaltsverzeichnis
Erstes Integral
Falls das Vektorfeld (p,q) eine Potentialfunktion F besitzt, muss es zu jeder Lösung obiger Differentialgleichung eine Konstante C geben, so dass die implizite Gleichung
erfüllt ist. Gelegentlich kann man diese implizite Gleichung explizit auflösen. In dieser Hinsicht ist diese implizite Version ein erster Schritt zum expliziten Lösen der Differentialgleichung. Aus diesem Grunde bezeichnet man F als erstes Integral der Differentialgleichung.
Integrierender Faktor
Für eine gewöhnliche Differentialgleichung der Form
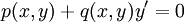 (wobei y nach x abgeleitet wird),
(wobei y nach x abgeleitet wird),
welche die Voraussetzung
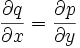 nicht erfüllt, lässt sich gelegentlich eine nullstellenfreie stetig differenzierbare Funktion
nicht erfüllt, lässt sich gelegentlich eine nullstellenfreie stetig differenzierbare Funktion 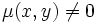 derart bestimmen, dass
derart bestimmen, dasseine exakte Differentialgleichung wird.
In diesem Fall bezeichnet man μ als integrierenden Faktor oder auch als eulerschen Multiplikator. Da μ niemals Null wird, hat diese Differentialgleichung dieselben Lösungen wie vor der Multiplikation mit μ.
Dabei ist μ(x,y) genau dann ein integrierender Faktor, wenn die partielle Differentialgleichung
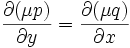 erfüllt wird.
erfüllt wird.Es ist normalerweise schwierig, diese partielle Differentialgleichung allgemein zu lösen. Da man aber nur eine spezielle Lösung μ(x,y) benötigt, wird man versuchen, mit speziellen Ansätzen für μ(x,y) eine Lösung zu finden. Solche Ansätze könnten beispielsweise lauten:
Ein solcher Ansatz führt meistens dann zum Ziel, wenn damit die partielle Differentialgleichung in eine gewöhnliche Differentialgleichung übergeht.
Kriterium für die Existenz integrierender Faktoren
Es gibt viele Kriterien, die integrierende Faktoren liefern. Prototypisch hierfür ist beispielsweise das folgende:
Der Definitionsbereich des Vektorfelds (p,q) sei ein einfach zusammenhängendes Gebiet des
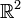 . Falls es eine Funktion
. Falls es eine Funktion 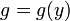 gibt, so dass
gibt, so dass  = g(y)p(x,y)](/pictures/dewiki/101/e62d7c9e44841f62a25eec9b048497e3.png) gilt, so ist jede nichttriviale Lösung μ = μ(y) von
gilt, so ist jede nichttriviale Lösung μ = μ(y) vonein integrierender Faktor.
Beweis
Die Gleichung
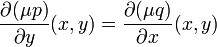 für
für 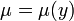 ist äquivalent zu
ist äquivalent zumit anderen Worten
Da die Nullfunktion eine Lösung von μ'(y) = g(y)μ(y) ist, besitzen alle anderen Lösungen nach dem Eindeutigkeitssatz keine Nullstellen. Somit ist μ ein integrierender Faktor.
Literatur
- Harro Heuser: Gewöhnliche Differentialgleichungen. Teubner 2004, ISBN 3519322277.
- Wolfgang Walter: Gewöhnliche Differentialgleichungen. Springer-Verlag 2000, ISBN 3540676422.
Wikimedia Foundation.

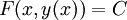
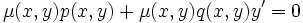
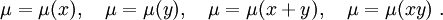
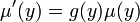
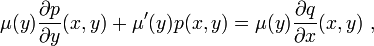
![\left[\mu'(y)-g(y)\mu(y)\right]\cdot p(x,y) = 0\ .](/pictures/dewiki/102/f9d2c701d51a3384608ef3f55a8027ae.png)