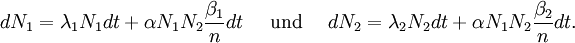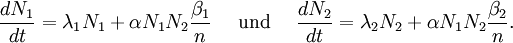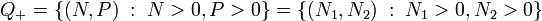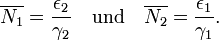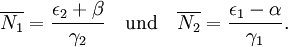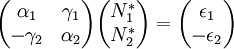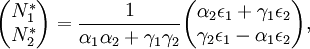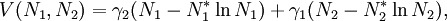Lotka-Volterra-Gleichung

Die Lotka-Volterra-Gleichungen, auch als Räuber-Beute-Gleichungen bekannt, sind ein System aus zwei nicht-linearen, gekoppelten Differentialgleichungen erster Ordnung und beschreiben die Wechselwirkung von Räuber- und Beutepopulationen. Unter Räuber und Beute sind dabei zwei Klassen von Lebewesen gemeint, wobei die eine sich von der anderen ernährt.^{[V 1]} Aufgestellt wurden die Gleichungen 1925 von Vito Volterra und, unabhängig davon, 1926 von Alfred James Lotka. Sie lauten

$\frac{dN_1}{dt} = N_1(\epsilon_1-\gamma_1N_2), \qquad \frac{dN_2}{dt} = -N_2(\epsilon_2-\gamma_2N_1)$

mit den Bezeichnungen^{[V 2]}

N1 = N1(t)	Anzahl der Beutelebewesen	zeitabhängig
ε1 > 0	Reproduktionsrate der Beute ohne Störung und bei großem Nahrungsangebot	konstant
N2 = N2(t)	Anzahl der Räuber	zeitabhängig
ε2 > 0	Sterberate der Räuber, wenn keine Beute vorhanden ist	konstant
γ1 > 0	Fressrate der Räuber pro Beutelebewesen = Sterberate der Beute pro Räuber	konstant
γ2 > 0	Reproduktionsrate der Räuber pro Beutelebewesen	konstant

Die Lotka-Volterra-Gleichungen sind eine wichtige Grundlage der Theoretischen Biologie, und darin insbesondere der Populationsdynamik. Bei den Räubern und der Beute muss es sich nicht unbedingt nur um Tiere oder einzelne Arten handeln; prinzipiell ist das Modell auf Gilden anwendbar – siehe z.B. Volterras Fischereidaten. Die Anwendbarkeit der Lotka-Volterra-Gleichungen hängt dabei davon ab, inwieweit die Begründung des mathematischen Modells im Einzelfall zutrifft.

Begründung des mathematischen Modells

Volterra begründet sein Gleichungssystem folgendermaßen^{[V 3]}:

• Die Populationszahlen der Beute bzw. der Räuber seien mit N₁ bzw. N₂ bezeichnet.
• Die ungestörten Wachstumsraten pro Zeiteinheit dt seien λ₁ und λ₂, wobei die Vorzeichen noch nicht fest liegen.
• Die (mittlere) Anzahl der Begegnungen zwischen Beute und Räuber pro Zeiteinheit dt ist αN₁N₂ mit einer positiven reellen Zahl α, die innerhalb eines Biotops als konstant angenommen wird, aber im allgemeinen vom Biotop abhängt.
• Eine genügend große Zahl n Begegnungen haben im Mittel einen Effekt β_i auf die Populationszahl N_i. Bei den Beutelebewesen ist das ohne weiteres klar: eine Begegnung mit einem Räuber führt mit einer gewissen Wahrscheinlichkeit dazu, dass die Beute gefressen wird. Dagegen ist die Auswirkung einer Begegnung auf die Zahl der Räuber nur indirekt, aber jedenfalls positiv; für die Modellbildung wird auch bei den Räubern eine sofortige Auswirkung auf die Populationszahl unterstellt.

Zusammengenommen führt das zu den Gleichungen

$dN_1 = \lambda_1 N_1 dt + \alpha N_1N_2 \frac{\beta_1}{n} dt\quad\mbox{ und }\quad dN_2 = \lambda_2 N_2 dt + \alpha N_1N_2 \frac{\beta_2}{n} dt.$

Division durch dt führt zu den Gleichungen

$\frac{dN_1}{dt} = \lambda_1 N_1 + \alpha N_1N_2 \frac{\beta_1}{n} \quad\mbox{ und }\quad \frac{dN_2}{dt} = \lambda_2 N_2 + \alpha N_1N_2 \frac{\beta_2}{n}.$

Setzt man

$\epsilon_1=\lambda_1,\quad\epsilon_2=-\lambda_2,\quad \gamma_1 = -\frac{\alpha\beta_1}n,\quad \gamma_2 = \frac{\alpha\beta_2}n,$

und macht man den Grenzübergang 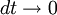$dt\to0$, so erhält man die Lotka-Volterra-Gleichungen in der eingangs genannten Form.

Mathematische Behandlung

Natürlich war auch Volterra klar, dass die zeitabhängigen Populationszahlen N₁(t) und N₂(t) nur ganzzahlige Werte annehmen können und daher als Funktionen von t entweder konstant oder nicht differenzierbar sind. Aber bei großen Populationszahlen ist der durch Übergang zum kontinuierlichen Modell gemachte relative Fehler gering. Der Vorteil der zweidimensionalen Lotka-Volterra-Gleichung ist jedoch, dass einige Aussagen mathematisch beweisbar sind, die einen interessanten Bezug zu realen Daten haben, wie weiter unten beschrieben ist.

Zur mathematischen Behandlung von Lotka-Volterra-Systemen benutzt man heute meist die etwas einfachere Notation^{[M 1]}

$\frac{dN}{dt} = N(a-bP),\quad \frac{dP}{dt} = P(cN-d),$

wobei a,b,c,d positive Konstanten sind und N(t) die Anzahl der Beutetiere und P(t) die Anzahl der Raubtiere (predators) bezeichnen.

Konstante Lösungen

Die konstanten Lösungen (auch Gleichgewichtspunkte oder kritische Punkte genannt) erhält man, indem man die rechten Seiten der Lotka-Volterra-Gleichungen gleich Null setzt:

$N(a-bP) = 0, \qquad P(cN-d) = 0.$

Es gibt also genau zwei konstante Lösungen, nämlich den trivialen Gleichgewichtspunkt (0,0) und den inneren Gleichgewichtspunkt

$(N^*,P^*)=\left(\frac{d}{c},\frac{a}{b}\right).$

Ein erstes Integral

Eine Methode zum Auffinden nicht-konstanter Lösungen besteht darin, ein erstes Integral, also eine Invariante der Bewegung, zu suchen. Volterra findet eine solche auf folgendem Weg^{[V 4]}: Multipliziert man die erste Grundgleichung mit c und die zweite mit b, und addiert anschließend die beiden Gleichungen, so verschwinden die Terme mit dem Produkt NP, und man erhält

$c\,\frac{dN}{dt} + b\, \frac{dP}{dt} = ac\,N-bd\,P$.

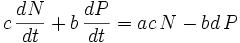Durch Multiplikation der ersten Grundgleichung mit d / N und der zweiten mit a / P und anschließender Addition kommt man zu

$\frac{d}{N}\,\frac{dN}{dt}+\frac{a}{P}\,\frac{dP}{dt} = ac\,N-bd\,P$.

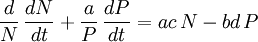Die numerisch berechneten Phasenraumtrajektorien zeigen einen Fixpunkt, um welchen Räuber- und Beute- Populationen zyklisch schwanken. Dabei bewegen sich die Lösungen auf den Niveaulinien von V.

Subtraktion dieser beiden Gleichungen ergibt

$c\,\frac{dN}{dt} - \frac{d}{N}\,\frac{dN}{dt} + b\,\frac{dP}{dt} - \frac{a}{P}\,\frac{dP}{dt} =0$.

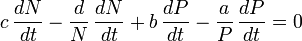Durch Integration dieser letzten Gleichung erreicht man schließlich die Beziehung

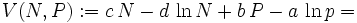$V(N,P) := c\,N - d\,\ln N + b\,P - a\,\ln p =$ const.

Umgekehrt kann man die totale Ableitung der so definierten Funktion V nach t berechnen:

$\begin{align} \frac{d}{dt}V(N,P) &= \frac{\partial V(N,P)}{\partial N}\cdot\frac{dN}{dt} + \frac{\partial V(N,P)}{\partial P}\cdot\frac{dP}{dt} \\ &= \left( c-\frac{d}{N}\right)\,N(a-bP) + \left( b-\frac{a}{P}\right)\,P(cN-d) \\ &= 0; \end{align}$

so gelangt man ebenfalls zu der Aussage, dass V auf den Lösungen der Grundgleichungen konstant (invariant) ist; eine Lösung der Lotka-Volterra-Gleichung kann also ihre Niveaulinien von V nicht verlassen.

Ein anderer Weg zum Auffinden einer Invarianten der Bewegung besteht darin, die Lotka-Volterra-Gleichungen mit Hilfe eines eulerschen Multiplikators in eine exakte Differentialgleichung umzuformen und diese dann zu integrieren.^{[W 1]}

Stabilität

Da V als erstes Integral auch eine Ljapunow-Funktion ist, und da V am inneren Gleichgewichtspunkt ein striktes lokales Minimum besitzt, folgt aus dem ersten Kriterium von Ljapunow, dass dieser Gleichgewichtspunkt stabil ist.

Die Lotka-Volterra-Gesetze

Mit Hilfe des ersten Integral V beweist Volterra^{[V 5]} drei mathematische Eigenschaften der Lösungen („Gesetze“) der Lotka-Volterra-Gleichungen, deren biologischen Interpretationen als Lotka-Volterra-Regeln Verbreitung gefunden haben.

Aus dem Randverhalten der Funktion V kann man schließen, dass keine Trajektorie, die einen Punkt im ersten Quadranten

$Q_+ = \{(N,P)\;:\;N>0, P>0\} = \{(N_1,N_2)\;:\;N_1>0,N_2>0\}$

besitzt, diesen verlässt: der erst Quadrant ist invariant. Die Lotka-Volterra-Gesetze gelten allgemein für maximale Lösungen der Lotka-Volterra-Gleichungen in diesem Quadranten; stirbt eine der beiden Tierklassen aus, so wird dieser Quadrant verlassen und die Lotka-Volterra-Gesetze verlieren ihre Gültigkeit.

Periodizität

Die Populationen über der Zeit aufgetragen ergibt das Bild einer Sinus-ähnlichen Schwingung mit einer Phasenverschiebung zwischen der Jäger- und der der Beutepopulation

Da die Funktion V im Quadranten Q ₊ strikt konvex ist und ihr Minimum im inneren Gleichgewichtspunkt annimmt, bilden die Niveaulinien von V geschlossene Kurven im Phasenraum. Da jede Lösung in einer Niveauline von V enthalten sein muss, folgt aus der Eindeutigkeit und einer Betrachtung des lokalen Richtungsfeldes die Periodizität der Lösungen. ^{[V 6][W 2]}

Loi du cycle périodique. – Les fluctuations des deux espèces sont périodique.

(Gesetz der periodischen Zykel: Die Schwankungen der beiden Klassen sind periodisch.)

Erhaltung der Mittelwerte

Aus der Periodizität der Lösungen folgt mit ein paar Zeilen Rechnung das

Loi de la conservation des moyennes. – Les moyennes pendant une période des nombres des individus des deux espèces sont independent des conditions initiales, et égales aux nombres qui correspondent à l'ètat stationnaire, pour les valeurs données des «coefficients d'accroissement» ε₁,ε₂, et des «coefficients de voracité» γ₁,γ₂.

(Gesetz der Erhaltung der Mittelwerte: Die zeitlichen Mittelwerte über eine Periode der Individuenzahlen der beiden Klassen hängen nicht von den Anfangsbedingungen ab, und sind gleich den Anzahlen des Gleichgewichtszustands, für die gegebenen „Wachstumskoeffizienten“ ε₁,ε₂, und die „Fresskoeffizienten“ γ₁,γ₂.)

Das bedeutet, die zeitlichen Mittelwerte erfüllen die Gleichungen

$\overline{N_1}=\frac{\epsilon_2}{\gamma_2}\quad\mbox{und}\quad\overline{N_2}=\frac{\epsilon_1}{\gamma_1}.$

Auf den ersten Blick verwirrend ist hier, dass der Mittelwert der Beutetierpopulation N₁(t) nur von Sterbe- und Fressrate der Raubtierpopulation und nicht von der Reproduktionsrate der Beutetiere abhängt. Dagegen ist der Mittelwert der Raubtierpopulation N₂(t) nur von Reproduktions- und Sterberate der Beutetierpopulation und nicht von Fress- und Sterberate der Raubtiere abhängig. Verständlich wird diese Eigenschaft des Lotka-Volterra-Modells, wenn man sich die hier zur Anwendung kommende Modellbildung ansieht: die Kontrolle über die Populationszahl der einen Tierklasse obliegt hier ausschließlich der jeweils anderen Klasse.

Störung der Mittelwerte

Das wegen seiner biologischen Interpretation interessanteste dieser Gesetze ist das

Loi de la perturbation des moyennes. – Si l'on détruit les deux espèces uniformément et proportionnellement aux nombres de leurs individus (assez peu pour que les fluctuations subsistent), la moyenne du nombres des individus de l'espèce dévorée croît et celles de l'espèce devorant diminue.

(Gesetz der Störung der Mittelwerte: Werden die beiden Tierklassen gleichmäßig und proportional zur Populationsgröße dezimiert, und ist die Rate der Dezimierung der Beute kleiner als deren Reproduktionsrate, so wächst der Mittelwert der Beutepopulation, und der Mittelwert der Räuberpopulation sinkt.)

Tatsächlich beweist Volterra eine quantitative Version: Ist α die Zerstörungsrate der Beutelebewesen, und β die Zerstörungsrate der Räuber, so sind die Mittelwerte für die Lösungen der gestörten Lotka-Volterra-Gleichungen

$\overline{N_1}=\frac{\epsilon_2+\beta}{\gamma_2}\quad\mbox{und} \quad\overline{N_2}=\frac{\epsilon_1-\alpha}{\gamma_1}.$

Das bedeutet: die über eine Lotka-Volterra-Periode gemittelte Anzahl der Beutelebewesen steigt genau dann an, wenn die Räuber dezimiert werden - ziemlich unabhängig von einer Dezimierung der Beute, solange diese nicht ausgerottet wird. Umgekehrt sinkt die mittlere Anzahl der Räuber immer dann, wenn die Beutelebewesen dezimiert werden, und dieses Absinken hängt nicht davon ab, wie stark die Räuber zusätzlich dezimiert werden (solange diese nicht ausgerottet weren).

Erweiterungen

In der theoretischen Ökologie bilden die Lotka-Volterra-Gleichungen den Ausgangspunkt zur Entwicklung komplexerer Modelle, von denen einige bereits in Volterras Buch beschrieben sind.

Intraspezifische Konkurrenzterme

Eine erste Erweiterung der Lotka-Volterra-Gleichungen entsteht durch Subtraktion von Termen proportional zu $N_1^2$ bzw. $N_2^2$, die die intraspezifische Konkurrenz modellieren.^{[W 3]} Es gibt verschiedene Möglichkeiten, die Form $-\alpha_1N_1^2$ und $-\alpha_2N_2^2$ der neu hinzugekommenen Terme zu begründen:

• Mit den empirischen Untersuchungen zur Bevölkerungsentwicklung nach Pierre-François Verhulst, siehe logistische Gleichung.
• Durch die Annahme, die (ungestörte) Wachstumsrate einer Population sei proportional zur Differenz zwischen einer Kapazitätsgrenze und der tatsächlichen Populationszahl.
• Durch eine Analyse des Einflusses von intraspezifischen Begegnungen auf die Populationszahl ähnlich zu Volterras Begründung des Terms zur Modellierungen der interspezifischen Konkurrenz: Eine intraspezifische Begegnung ist mit einer gewissen Wahrscheinlichkeit eine Konkurrenz um eine Ressource, bei der ein Individuum den Kürzeren zieht.

Man kommt so zu Gleichungen der Form

$\begin{align}\frac{dN_1}{dt} &= N_1(\epsilon_1-\gamma_1N_2-\alpha_1N_1), \\ \frac{dN_2}{dt} &= N_2(-\epsilon_2+\gamma_2N_1-\alpha_2N_2),\end{align}$

die wiederum zwei Gleichgewichtslagen zulassen: den trivialen Gleichgewichtspunkt (0,0), und den inneren Gleichgewichtspunkt 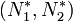$(N_1^*,N_2^*)$, der durch ein lineares Gleichungssystem gegeben ist:

$\begin{pmatrix} \alpha_1 & \gamma_1 \\ -\gamma_2 & \alpha_2 \end{pmatrix} \begin{pmatrix}N_1^*\\ N_2^*\end{pmatrix} = \begin{pmatrix}\epsilon_1\\ -\epsilon_2\end{pmatrix}$

Durch Lösen dieses Gleichungssystems findet man den Gleichgewichtspunkt

$\begin{pmatrix}N_1^*\\ N_2^*\end{pmatrix} =\frac1{\alpha_1\alpha_2+\gamma_1\gamma_2} \begin{pmatrix} \alpha_2\epsilon_1+\gamma_1\epsilon_2\\ \gamma_2\epsilon_1-\alpha_1\epsilon_2\end{pmatrix},$

der unter der Bedingung γ₂ε₁ > α₁ε₂ im ersten Quadranten liegt.

Zu diesem erweiterten Lotka-Volterra-Systems gibt es auch eine Ljapunow-Funktion:

$V(N_1,N_2) = \gamma_2(N_1-N_1^*\ln N_1) + \gamma_1(N_2-N_2^*\ln N_2),$

mit der die Voraussetzungen des Zweiten Kriteriums von Ljapunow für den Gleichgewichtspunkt 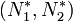$(N_1^*,N_2^*)$ erfüllt sind. Darauws folgt, dass dieser Gleichgewichtspunkt jetzt asymptotisch stabil ist. ^{[W 4]}

Mehr als zwei Klassen von Lebewesen

Ein großer Teil von Volterras Buch^{[V 7]} bezieht sich auf Erweiterungen seines Systems auf mehr als zwei Klassen von Lebewesen, die in unterschiedlichen Weisen miteinander interagieren.

Anwendungen

Fischereidaten

In der Einleitung zu Volterras Buch^{[V 8]} findet sich eine Tabelle, die zu den Jahren 1905 und 1910-1923 und zu drei Fischereihäfen jeweils den prozentualen Anteil der Knorpelfische (Sélaciens), also insbesondere der Haie, am gesamten Fischfangs des Fischereihafens enthält:

	1905	1910	1911	1912	1913	1914	1915	1916	1917	1918	1919	1920	1921	1922	1923
Trieste	-	5,7	8,8	9,5	15,7	14,6	7,6	16,2	15,4	-	19,9	15,8	13,3	10,7	10,2
Fiume	-	-	-	-	-	11,9	21,4	22,1	21,2	36,4	27,3	16	15,9	14,8	10,7
Venise	21,8	-	-	-	-	-	-	-	-	-	30,9	25,3	25,9	26,8	26,6

«Cela prouve pendant la période 1915-1920, où la pêche était moins intense à cause de la guerre, un accroissement relatif de la classe des Sélaciens qui, particulièrement voraces, se nourissent d'autres poissons. Les statistique inclinent donc à penser qu'une diminution dans l'intensité de la destruction favorise les espèces les plus voraces.» ^{[V 9]}

Diese Statistiken zeigen in den Jahren 1915 bis 1920, als der Fischfang im Mittelmeer wegen des ersten Weltkriegs weniger intensiv war, einen erhöhten Anteil an Raubfischen, der dann mit der Intensivierung der Fischerei nach 1920 wieder zurückgeht. Das dritte Lotka-Volterra-Gesetz, die Verschiebung der Mittelwerte, bietet hierfür eine plausible Erklärung.

Medizinische Epidemiologie

In der Theoretischen Biologie sowie in der medizinischen Epidemiologie finden Modelle vom Loltka-Volterra-Typ zur Beschreibung der Ausbreitungsprozesse von Krankheiten Verwendung. Einige Beispiele finden sich in SI-Modell, SIR-Modell und SIS-Modell.

Siehe auch

• Wator (Räuber-Beute-System modelliert als Zellulärer Automat)
• Logistische Gleichung (Grundgleichung des beschränkten Populationswachstums)

Literatur

• Lotka, Alfred J.: Analytical Theory of Biological Populations, Springer New York 1998, ISBN 978-0-306-45927-6, englische Übersetzung der beiden Bände
  • Théorie analytique des associations biologiques. Première partie. Principes (1934)
  • Théorie analytique des associations biologiques. Deuxième partie. Analyse démographique avec application particulière à l'espèce humaine (1939)

Humor

Der israelische Astrophysiker Nir Shaviv vergleicht den Gegensatz zwischen Shas und Shinui in der israelischen Politik mit einem Jäger-Beute Mechanismus nach der Lotka-Volterra-Gleichung. Das israelische Grundproblem sei, dass ein Drittel der Bevölkerung arbeite, eines Steuern zahlte und das dritte Reseverübungen ableiste und es sich bei allen dreien um ein und dasselbe Drittel handele - was nach Ansicht des säkularen Israeli Shaviv von Shinui vertreten werde. ^[1]

Einzelnachweise

1. ↑ Sciencebits Darstellung von Shaviv

• Vito Volterra: Leçons sur la Théorie Mathématique de la Lutte pour la Vie, Éditions Jaques Gabay 1990, ISBN 2-87647-066-7, autorisierter Nachdruck der bei Gauthier-Villars 1931 erschienen Originalausgabe.

1. ↑ chap. I, sec. II. Deux espèces dont l'une dévore l'autre
2. ↑ p. 14
3. ↑ p. 14f
4. ↑ p. 15
5. ↑ p. 15–27
6. ↑ p. 15–19
7. ↑  
8. ↑ Seite 2 ff.
9. ↑ p. 2

• James D. Murray, Mathematical Biology I: An Introduction. Springer, third edition, corrected printing 2008, ISBN 978-0-387-95223-9

1. ↑ p. 79

• Günther J. Wirsching: Gewöhnliche Differentialgleichungen, Teubner Lehrbuch 2006, ISBN 978-3-519-00515-5

1. ↑ Beispiel 4.2, Seite 65 ff.
2. ↑ Seiten 67–70
3. ↑ Seiten 80 ff.
4. ↑ Seite 82