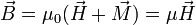- Ferromagnetisch
-
Ferromagnetismus (von lat.: ferrum = Eisen + Magnet) ist die „normale“ Form des Magnetismus, so wie er z. B. in Hufeisen- und Kühlschrankmagneten auftritt. Die Anziehungskraft zwischen einem Magneten und einem ferromagnetischen Material ist verantwortlich für den Großteil der magnetischen Erscheinungen des Alltags.
Inhaltsverzeichnis
Grundlagen
Ein Material wird „ferromagnetisch“ genannt, wenn es, nachdem es einem externen Magnetfeld ausgesetzt wurde, selbst zum Magneten wird. Dabei wird zwischen ‚magnetisch harten‘ und ‚weichen‘ Stoffen unterschieden. Die ‚harten‘ Stoffe weisen eine hohe Koerzitivfeldstärke auf, die ,weichen' eine kleine Koerzitivfeldstärke. Fälschlicherweise geht man häufig davon aus, dass eine hohe Remanenz auf einen magnetisch harten Stoff schließen lässt. Die Remanenz hängt allerdings nur davon ab, wie die magnetischen Momente im Vergleich zum äußeren Feld "stehen wollen". Ist die Anisotropie der magnetischen Momente in Richtung des äußeren Feldes, so ist die Remanenz sehr groß (ungefähr Sättigungsmagnetisierung). Wollen die magnetischen Momente allerdings senkrecht zum äußeren Feld stehen, so ist die Remanenz Null, da die Momente in die Ebene senkrecht zum externen Feld relaxieren und somit keinen Beitrag zur Hysteresekurve liefern. In Bulkmaterialien sind die magnetischen Momente "wild verteilt", wodurch dieses typische Bild der "schiefen" Hysteresekurve zustandekommt.
Die bekanntesten ferromagnetischen Stoffe bei Raumtemperatur sind Eisen, Cobalt und Nickel. Die meisten Metalle sind nicht ferromagnetisch und sind daher weder (in ferromagnetischer Weise) magnetisierbar, noch werden sie von einem Magneten angezogen, z. B. Aluminium, Kupfer, Messing, Silber, Gold. Im Alltag lässt sich daher mit einem Magneten leicht prüfen, ob ein metallener Gegenstand aus Eisen ist oder nicht. Eine Ausnahme hiervon stellen austenitische Legierungen dar, die Bestandteil vieler nichtrostender Stähle sind. Ein austenitisches Gefüge ist nicht ferromagnetisch, obwohl es hauptsächlich aus Eisen besteht.
Die Anziehungskraft zwischen einem Magneten und einem ferromagnetischen Stoff
Gelangt ein ferromagnetischer Gegenstand in ein Magnetfeld (z. B. in den Nahbereich eines Permanentmagneten), so richten sich die Elementarmagnete (die Kernspinzustände der Atome in seinem Metallgitterverband) entsprechend diesem Magnetfeld aus. Dadurch wird der Gegenstand nun selbst magnetisch. Die beiden Magnetfelder haben die gleiche Ausrichtung, daher entsteht zwischen dem Gegenstand und dem Magneten eine magnetische Anziehungskraft. Ein ferromagnetisches Material wird aus diesem Grund sowohl von magnetischen Nordpolen als auch von Südpolen angezogen.
Im Normalfall verliert sich diese Magnetisierung zum größten Teil sofort, wenn der Gegenstand wieder aus dem externen Magnetfeld entfernt wird. Lediglich ein kleiner Restmagnetismus bleibt zurück, die so genannte Remanenz. Es gibt jedoch auch Materialien, bei denen eine dauerhafte (permanente) starke Magnetisierung erreicht werden kann. Solche ferromagnetischen Körper, z. B. aus gehärtetem Stahl, können zu Permanentmagneten magnetisiert werden, das heißt, eine deutliche erkennbare (makroskopische) Magnetisierung dauerhaft annehmen.
Alle Permanentmagnete sind entweder ferromagnetisch oder ferrimagnetisch, ebenso die Metalle, die deutlich von ihnen angezogen werden. Ferromagnetische Festkörper, die magnetisiert sind, bezeichnet man als Ferromagnete.
Entstehen von Ferromagnetismus
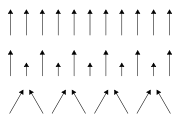
Ferromagnetismus entsteht dadurch, dass elementare magnetische Momente eine parallele Ordnung aufweisen. Die Bereiche gleicher Magnetisierung werden Domänen oder Weiss-Bezirke genannt. Sie treten in Größen von 0,01 µm bis 1 µm auf und sind im unmagnetisierten Zustand der Substanz nicht einheitlich orientiert. Die Ausrichtungsprozesse der Domänen werden Barkhausensprünge genannt.
Die magnetische Ordnung wird bei hohen Temperaturen aufgebrochen, die Ferromagneten sind dann nur noch paramagnetisch. Die Temperatur, oberhalb derer die ferromagnetische Ordnung verschwindet, wird als Curie-Temperatur TC (nach Pierre Curie, dem Gatten von Marie Curie) bezeichnet. Der Paramagnetismus bleibt für alle Temperaturen oberhalb der Curie-Temperatur erhalten, selbst nach Übergang des Festkörpers in die Flüssigkeits- oder Gasphase.
Stoffe mit ferromagnetischen Eigenschaften
Substanz TC in K Co 1395 Fe 1033 Ni 627 CrO2 390 Gd 289 Dy 85 EuO 70 Ho 20 Unter den Elementen bzw. Metallen in Reinform weisen Eisen, Kobalt und Nickel bei Raumtemperatur ferromagnetische Eigenschaften auf. Bei tieferen Temperaturen werden auch die Lanthanoide Gadolinium, Terbium, Dysprosium, Holmium und Erbium ferromagnetisch.
In der Praxis verwendet man häufig ferromagnetische Legierungen wie z. B. AlNiCo, SmCo, Nd2Fe14B, NiFe („Permalloy“), oder NiFeCo („Mumetall“). Bemerkenswert ist, dass unter bestimmten Umständen auch einige Verbindungen im Allgemeinen nicht ferromagnetischer Elemente ferromagnetisches Verhalten aufweisen, beispielsweise Chromdioxid, Manganarsenid, Europium(II)-oxid oder die suprafluide A-1 Phase von He-3.
Ebenfalls bemerkenswert ist, dass der bekannteste ferromagnetische Stoff, Eisen, als Hauptbestandteil einer austenitischen Legierung nicht ferromagnetisch wirkt. Austenitische Gefüge sind Bestandteil vieler nichtrostender Stähle und von Edelstahl-Sorten.
Physikalischer Ursprung
Träger der elementaren magnetischen Momente sind die Elektronenspins. Wie bei anderen kooperativen magnetischen Phänomenen ist auch beim Ferromagnetismus die magnetische Wechselwirkung viel zu schwach, um für die Ordnung der Spins verantwortlich zu sein. Bei der ferromagnetischen Ordnung kommt noch hinzu, dass die parallele Ausrichtung magnetischer Momente für die magnetische Wechselwirkung energetisch ungünstig ist. Verantwortlich für die parallele Spinordnung des Ferromagneten ist die so genannte Austauschwechselwirkung, die mit der Existenz von Singulett- und Triplett-Zuständen bei Zwei-Elektronen-Systemen zu tun hat und mit dem Pauli-Prinzip zusammenhängt. Es handelt sich also um ein echt quantenmechanisches Phänomen, das nicht einfach zu verstehen ist.
Im Detail muss nach dem Pauli-Prinzip für eine antisymmetrische Ortswellenfunktion die zugehörige Spinwellenfunktion symmetrisch sein (z. B. bei parallelen Spins im Zwei-Elektronen-System). Man kann zeigen, dass der durchschnittliche Abstand der beiden Teilchen bei einer antisymmetrischen Ortswellenfunktion größer ist und damit für Teilchen gleicher Ladung deren Coulomb-Abstoßung geringer. Die Austauschwechselwirkung bewirkt hier also eine effektive Absenkung der potentiellen Energie. Andererseits können sich die Elektronen mit parallelem Spin nach dem Pauli-Prinzip nicht im selben Zustand befinden und müssen sukzessive höhere Niveaus besetzen, wodurch ihre kinetische Energie zunimmt. Die spontane Parallelstellung der Spins und damit eine ferromagnetische Ordnung wird also nur zustande kommen, wenn die Absenkung der potentiellen Energie die Erhöhung der kinetischen Energie überkompensiert.
Eine anschauliche Darstellung hierzu gibt die Bethe-Slater-Kurve, welche die Austauschwechselwirkung in Abhängigkeit vom relativen Atomabstand zeigt. Der relative Atomabstand ist hierbei das Verhältnis des Atomabstandes der benachbarten Atome zum Durchmesser der nicht abgeschlossenen Elektronenschale.
In einem Satz: „Die Ordnung der magnetischen Momente wird durch die (quantenmechanische!) Austauschwechselwirkung vermittelt, nicht durch (klassische!) magnetische Wechselwirkung.“
Die magnetische Leitfähigkeit μ = μ0(1 + χ) und damit die Magnetische Suszeptibilität χ ist bei Ferromagneten nicht konstant, sondern eine komplizierte Funktion der angelegten Feldstärke und von der Magnetisierungs-Vorgeschichte abhängig. Meist wird daher die (differentielle) magnetische Suszeptibilität χ als Ableitung der Magnetisierung nach der Feldstärke betrachtet. Sie verschwindet im Sättigungsbereich.
Die Magnetisierung steht mit der magnetischen Flussdichte
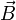 über
überin Verbindung, mit
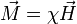 .
.
Sättigung
Unter Sättigungsmagnetisierung versteht man jene Magnetisierung M, bei der in einem meist ferromagnetischen Stoff eine Erhöhung der äußeren magnetischen Feldstärke H keine Erhöhung der Magnetisierung des Stoffes mehr bewirkt. Dieser hat einen konstanten, materialspezifischen „Sättigungswert“ erreicht. Anders ausgedrückt wird die (differentielle) magnetische Suszeptibilität χ als Ableitung der Magnetisierung nach der Feldstärke betrachtet. Sie verschwindet im Sättigungsbereich.
Eine besonders gute Leitfähigkeit für den magnetischen Fluss Φ ist die wesentliche Eigenschaft vor allem ferromagnetischer Werkstoffe wie beispielsweise Weicheisen, Dynamoblech oder bestimmter Ferrite. Dies begründet den Einsatz dieser Werkstoffe, wo es auf die räumliche Führung von magnetischen Flüssen ankommt, beispielsweise in Eisenkernen von Transformatoren. Durch eine Steigerung der magnetischen Flussdichte in diesen Materialien wird der Bereich der Sättigungsmagnetisierung erreicht, wo es zu einem starken Abfall der magnetischen Leitfähigkeit kommt. Die magnetische Sättigung ist bei diesen technischen Anwendungen daher meist unerwünscht.
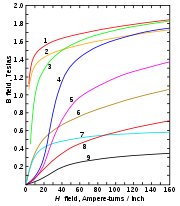
Trägt man bei einem Werkstoff die magnetische Flussdichte B gegenüber der von außen aufgebrachten magnetischen Feldstärke H in einem Diagramm auf, ergibt sich die Magnetisierungskurve. Die Abflachung der Steigung kennzeichnet dabei anschaulich den Beginn der Sättigungsmagnetisierung
Material Flussdichte in Tesla bei welcher
die magnetische Sättigung einsetztCobalt-Eisen
Fe mit 47 bis 50 % Co2,35 Silicium-Eisen
Fe mit 3 bis 4 % Si1,5 bis 2 Nickel-Eisen
Fe mit 30 bis 50 % Ni1,2 bis 1,5 Ferrit (MnZn) 0,4 Ferrit (NiZn) 0,2 Praxisbezüge
- Geophysik: Identifizierung von Materialien durch Ermittlung der spezifischen Curie-Temperatur, indem man die Abhängigkeit der Sättigungsmagnetisierung von der Temperatur bestimmt.
- In technischen Anwendungen wie Transformatoren oder Elektromotoren ist die magnetische Sättigung des Kerns unerwünscht und führt zu einem massiven Abfall des Wirkungsgrades und der übertragenen Leistung. Um eine Sättigung zu vermeiden, müssen magnetische Kerne in Transformatoren und Elektromotoren eine entsprechende Mindest-Querschnittsfläche aufweisen.
- In magnetischen Spannungskonstantern wird die magnetische Sättigung eines Transformatorkerns genutzt, um kurzzeitige Schwankungen in problematischen Stromnetzen zu stabilisieren.
Hysterese
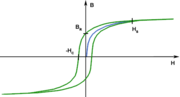
Der Begriff Hysterese (griech.: hysteros = hinterher, später) charakterisiert ein System, dessen veränderliche Ausgangsgröße nicht allein von der Eingangsgröße abhängig ist, sondern auch von deren Verlaufsgeschichte. Ein solches Hystereseverhalten tritt auch bei ferromagnetischen, magnetisch leitfähigen Stoffen wie Eisen, Kobalt und Nickel und deren Legierungen auf.
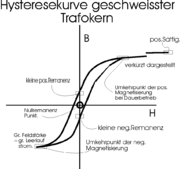
Die magnetische Flußdichte in einem ferromagnetischen Stoff wird von der Stärke des umgebenden Magnetfeldes (H) bestimmt. Wird H genügend erhöht, steigt B wegen der Sättigung von B nur noch sehr geringfügig an. Geht das äußere Magnetfeld zurück, so nimmt die Flußdichte wieder ab. Die magnetische Flußdichte erreicht bei dem gleichen Wert einer Feldstärke, die im Abnehmen begriffen ist, einen höheren Wert als er während des Zunehmens der Feldstärke auftrat. Wird H gänzlich auf Null gesenkt, geht B nicht auf Null zurück, sondern nur bis zur sogenannten Remanenz BR. Um den Stoff wieder zu entmagnetisieren, muss daher ein entgegengesetztes Magnetfeld mit der Koerzitivfeldstärke − HC aufgebaut werden. Die vollständige Entmagnetisierung gelingt jedoch nicht in einem Schritt. Ein erneutes Umkehren der Feldstärke von H führt dazu, dass der untere Ast der Hysteresekurve durchlaufen wird. Dieser Hysteresevorgang lässt sich gut am Verlauf der Hysteresekurve oder Hystereseschleife verdeutlichen. Ein vollständiges Durchlaufen der Hysteresekurve wird als Hysteresezyklus bezeichnet. Nur ein in der Amplitude abklingendes magnetisches Wechselfeld führt durch die allmähliche Annäherung der Hysteresezyklen an den Nullpunkt zur vollständigen Entmagnetisierung.
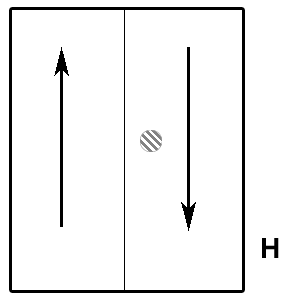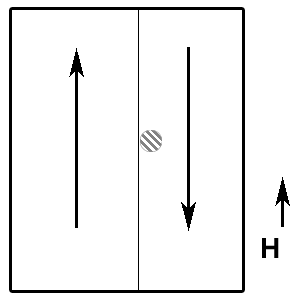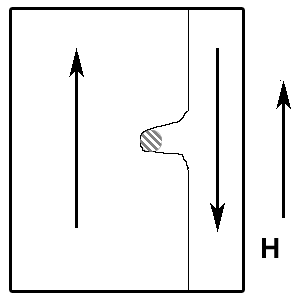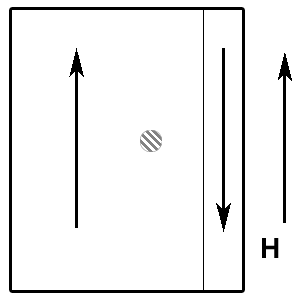
Die Ursache für das Verhalten sind die sogenannten Weiss-Bezirke. Sie zeichnen sich dadurch aus, dass die Spins der Elektronen, die als Elementarmagnete aufgefasst werden können, innerhalb eines Bezirks parallel zueinander sind. Die Grenzen zwischen den Bezirken heißen Bloch-Wände. Wird nun ein äußeres Magnetfeld angelegt, so wachsen die Bezirke, deren Orientierung der Ausrichtung des Magnetfeldes entspricht, auf Kosten der anderen Bezirke, indem Elektronen in den anderen Bezirken „umklappen“, sich also parallel zum Magnetfeld ausrichten. Anschaulich entspricht das einer Verschiebung der Bloch-Wände.
Störstellen, die in jedem Ferromagnetikum existieren, (in Eisen z. B. Kohlenstoffeinschlüsse) verhindern jedoch, dass das Verschieben der Bloch-Wände gleichmäßig verläuft. Wenn eine Bloch-Wand beim Verschieben auf eine Störstelle trifft, so bleibt sie zuerst an ihr hängen, und es bildet sich hinter der Störstelle eine Art Blase, in der die Spins der Elektronen noch nicht umklappen. Erst ab einer bestimmten Feldstärke schließt sich diese Blase, was zu einer plötzlichen Änderung der Magnetisierung führt. Dieser Vorgang wird Barkhausen-Sprung genannt. Durch diese ungleichmäßigen Wandverschiebungen wird eine Entmagnetisierung entlang der Neukurve unmöglich. Sie sind der Grund für das Entstehen der Hysteresiskurve.
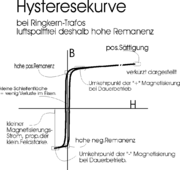
Wenn alle Elektronenspins im Ferromagnetikum an dem Feld ausgerichtet sind, ist die Sättigung erreicht. Wird nun das äußere Feld entfernt, kehren nicht alle Elektronen zur ursprünglichen Ausrichtung zurück. Die Magnetisierung sinkt bis auf das Remanenz-Niveau ab. Erst durch die Zufuhr zusätzlicher Energie kann der Stoff wieder entmagnetisiert werden. Stoffe mit hoher Remanenz sind nicht zwingend hartmagnetisch. Hartmagnetische Stoffe (Dauermagnete) benötigen eine hohe Koerzitivfeldstärke. Die Remanenz in einem Transformatorkern ist weniger von dem Kernmaterial abhängig, sondern hängt stark von der Bauform des Kernes ab: Ein Ringkerntransformator-Kern hat eine sehr hohe Remanenz, weil keinerlei Luftspalte im Magnetkreis liegen. Ein Transformator mit technologisch bedingten oder absichtlich eingebauten Luftspalten hat dagegen durch Scherung, (Neigung), der Hysteresekurve eine geringe Remanenz, obwohl das Kernmaterial selbst eine hohe Remanenz besitzen kann.Das Integral unter der durchlaufenen Hysteresiskurvenfläche entspricht der Energie, die im Stoff bei seiner vollständigen Ummagnetisierung in Wärme umgewandelt wird. Bei elektromagnetischen Bauteilen machen sie sich als "Ummagnetisierungsverluste" bzw. zusätzlicher Energieaufwand bemerkbar. Dieses Integral sollte im Fall von Speichermedien möglichst hoch sein. Im Fall von Kernen von Transformatoren sollte es möglichst klein sein, um nur geringe Energieverluste zu verursachen. Für andere Zusammenhänge gilt das in ähnlicher Weise. Typisch für die Hysterese ist das Auftreten von bistabilem Verhalten. Bei gleichen Umgebungsbedingungen ist der Zustand von der Vergangenheit, der wirkenden Spannungszeitfläche vor dem Ausschalten abhängig. Entsprechend wird ein bestimmter Punkt im Zustandsdiagramm erreicht.
Unter Berücksichtigung der Form der Hysteresisschleife kann man einen Stoff gezielt aufmagnetisieren. Dieses findet Anwendung bei der Herstellung von Dauermagneten oder beim Beschreiben von magnetischen Speichermedien (Magnetband, Festplatte, Kernspeicher). Im Falle hoher Koerzitivfeldstärken spricht man von magnetisch hartem Material, da zu ihrer Neuorientierung hohe Feldstärken benötigt werden. Bei Speichermedien entspricht dieses einer hohen Datensicherheit, da die geschriebenen Informationen nicht zufällig durch Streufelder umorientiert werden. Bei geringen Koerzitivfeldstärken spricht man von magnetisch weichem Material. Die Bezeichnungen rühren daher, dass reines (also weiches) Eisen im Vergleich zu magnetischen Stählen eher weichmagnetisch ist.
Praxisbezüge
- Der Verlauf und die Form einer Hysteresekurve wird nicht nur durch das Material des Magnetfeldleiters, wie zum Beispiel Verlustarmut, Kornorientierung und deren Ausrichtung zu den Feldlinien, sondern auch stark durch seine Bauform, vor allem mit oder ohne Luftspalte beeinflusst.
- Bei den früher üblichen Kernspeichern der Computer wurden Speicherringe, die häufig ihren Zustand wechselten, warm und reagierten anders auf die Stromimpulse als Speicherringe, die selten angesprochen wurden. Abhilfe war eine kräftige Umwälzung der Luft, damit alle Kerne möglichst gleiche Temperatur hatten.
- In vielen Anwendungen werden kleine Hysteresezyklen um Punkte in der B-H-Fläche gefahren; siehe auch Kleinsignalverhalten. Aufgrund der von der Magnetisierung abhängigen Permeabilität weisen Zyklen nahe dem Ursprung eine höhere Permeabilität auf.
- Wichtig ist die Hysterese-Eigenschaft beispielsweise in der Audiotechnik bei der Aufnahme auf Tonband (siehe Tonband, Vormagnetisierung).
- Für das Verständnis sowie die Auslegung und Berechnung von Transformatoren ist die Kenntnis des Hystereseverhaltens des Kernmaterials grundlegend wichtig.
- Wenn Materialien ummagnetisiert werden, muss Energie für die veränderte Ausrichtung der Weiss-Bezirke aufgewendet werden. Dieses Drehen verursacht Wärme im Eisen (Hytereseverluste).
Domänen
Die Austauschwechselwirkung wirkt nur zwischen Fermionen, deren Wellenfunktionen einen wesentlichen Überlapp aufweisen, in der Regel also nur zwischen nahegelegenen Teilchen. Die magnetische Wechselwirkung wirkt hingegen auch zwischen weit entfernt liegenden magnetischen Momenten. Daher steigt in einem ausgedehnten Ferromagneten der magnetische Energieaufwand irgendwann über den Energiegewinn der Austauschwechselwirkung. Die ferromagnetische Ordnung des Festkörpers zerfällt dann in unterschiedlich orientierte Domänen. Die Bereiche des Festkörpers, in denen unterschiedlich orientierte Domänen aufeinandertreffen, heißen Domänenwand. Je nach Drehsinn der Magnetisierung in der Wand spricht man von Bloch-Wand oder Néel-Wand. Die Ausbildung der Domänenwand erfordert die Verrichtung von Arbeit gegen die Austauschwechselwirkung, die Verkleinerung der Domänen (des Volumens einer zusammenhängenden Domäne) reduziert die magnetische Energie eines Festkörpers. Diese Arbeit kann aus der Fläche der Hystereseschleife berechnet werden. Aufgrund der nicht kontinuierlich erfolgenden Ausrichtung der Weiss-Bezirke unter dem Einfluss äußerer Magnetfelder können sog. Barkhausen-Sprünge beobachtet werden.
Anwendung
Ferromagnetische Werkstoffe weisen eine hohe Permeabilität mit μr ≥ 1 auf. Dadurch werden die magnetischen Feldlinien gut im Vergleich zum umgebenden Material (etwa Luft mit μr ≈ 1) geleitet. Dadurch finden ferromagnetische Werkstoffe etwa in Elektromagneten und Transformatoren Verwendung.
siehe auch: Permeabilitätszahl
Literatur
- Horst Stöcker: Taschenbuch der Physik. 4. Auflage, Verlag Harry Deutsch, Frankfurt am Main 2000, ISBN 3-8171-1628-4
- Hans Fischer: Werkstoffe in der Elektrotechnik. 2. Auflage, Carl Hanser Verlag, München/Wien 1982, ISBN 3-446-13553-7
- Günter Springer: Fachkunde Elektrotechnik. 18.Auflage, Verlag - Europa - Lehrmittel, Wuppertal 1989, ISBN 3-8085-3018-9
- Richard P. Feynman, Robert B. Leighton, Matthew Sands: Vorlesungen über Physik. 3. Auflage, Oldenbourg Verlag, München/Wien 2001, ISBN 3-486-25589-4
Siehe auch
Wikimedia Foundation.