Permeabilität (Magnetismus)

Physikalische Größe
Name	magnetische Leitfähigkeit
Formelzeichen der Größe	μ
Größen- und Einheiten- system Einheit Dimension SI H · m−1 = V · s · A−1· m−1 = N · A−2 = m · kg · s−2 · A−2 L · M · T−2 · I–2
Siehe auch: Magnetische Feldkonstante

Vereinfachter Vergleich der Permeabilitäten von ferromagnetischen (μ_f), paramagnetischen (μ_p) und diamagnetischen Materialien (μ_d) zu Vakuum (μ₀)

Die magnetische Permeabilität μ (auch magnetische Leitfähigkeit) bestimmt die Durchlässigkeit von Materie für magnetische Felder. Sie ist eine abgeleitete SI-Größe mit enger Verwandtschaft zur magnetischen Suszeptibilität.

Grundlagen

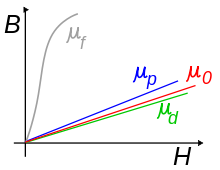
Anders ausgedrückt heißt das Verhältnis der magnetischen Flussdichte B zur magnetischen Feldstärke H Permeabilität.

$\vec{B} = \mu \, \vec{H}$

Die magnetische Feldkonstante μ₀ ist eine physikalische Konstante und gibt die magnetische Permeabilität des Vakuums an. Auch dem Vakuum ist eine Permeabilität zugewiesen, da sich auch dort Magnetfelder einstellen oder elektromagnetische Felder ausbreiten können. Die Permeabilitätszahl μ_r, früher auch als relative Permeabilität bezeichnet, ist das Verhältnis von μ zur magnetischen Feldkonstante μ₀.

$\mu_r = \frac{\mu}{\mu_0}$

Für das Vakuum ergibt sich folglich eine Permeabilitätszahl von 1. Die dimensionslose Größe μ_r hängt mit der magnetischen Suszeptibilität χ zusammen über folgende Beziehung:

μ_r = 1 + χ

Komplexe Permeabilität, Permeabilitätszahl

Vor allem in der Elektrotechnik werden zur Erfassung zeitabhängiger Effekte Phasoren für die Felder und entsprechend eine komplexe Permeabilität benutzt.

$\hat{\mu} = {\mu_s}' - \mathrm j \cdot {\mu_s}''$

Der Realteil der komplexen Permeabilität μ_s' entspricht der normalen Permeabilität. Der Imaginärteil μ_s'' hingegen beschreibt die Größe der Ummagnetisierungsverluste.

Mit Ausnahme der ferromagnetischen Materialien mit einer deutlich höheren relativen Permeabilität als eins, ist auch der Imaginärteil der komplexen Permeabilität vernachlässigbar, ebenso die Frequenzabhängigkeit der Permeabilität. Es ergibt sich eine skalare, frequenzunabhängige Permeabilität:

$\mu = \mu_0 \cdot \mu_r$

Bei ferromagnetischen Materialien kann die Frequenzabhängigkeit für viele technische Anwendungen nicht vernachlässigt werden, es ergibt sich:

$\hat{\mu}\,(f) = {\mu_s}'\,(f) - \mathrm j \cdot {\mu_s}''\,(f)$

wobei f die Frequenz des magnetischen Wechselfeldes ist. Der Imaginärteil μ_s''(f) ist direkt der Bewegung der Bloch-Wände im Material zugeordnet und bei einer Resonanz ergibt sich ein Maximum, in der Regel im Bereich 10–1000 kHz.

Wie viele physikalischen Materialeigenschaften ist auch die komplexe Permeabilität in der verallgemeinerten Form eigentlich ein dreidimensionaler Tensor zweiter Stufe. Bei den meisten Materialien ist die Anisotropie der magnetischen Eigenschaften aber so klein, dass eine Beschreibung als skalare, komplexe Permeabilität ausreichend ist.

Klassifizierung

Permeabilitätszahlen für ausgewählte Materialien

Medium	µr	Einteilung
Supraleiter	0	ideal diamagnetisch
Blei, Zinn	< 1 (ca. 0,999…)	diamagnetisch
Kupfer	0,9999936 = 1 − 6,4·10−6	diamagnetisch
Wasserstoff	1 - 2,061·10−9	diamagnetisch
Vakuum	1	(neutral)
Luft	ca. 1 + 0,4·10−6	paramagnetisch
Aluminium	1 + 2,2·10−5	paramagnetisch
Platin	1+ 2,57·10−4	paramagnetisch
Kobalt	80…200	ferromagnetisch
Eisen	300…10.000	ferromagnetisch
Ferrite	4…15.000	ferromagnetisch
Mumetall (NiFe)	50.000…140.000	ferromagnetisch
amorphe Metalle (ferromagnetisch)	700…500.000	ferromagnetisch
nanokristalline Metalle (ferromagnetisch)	20.000…150.000	ferromagnetisch

Magnetische Materialien lassen sich anhand ihrer Permeabilitätszahl klassifizieren.

Diamagnetische Stoffe $0 \leq \mu_r <1$

Diamagnetische Stoffe besitzen eine geringfügig kleinere Permeabilität als das Vakuum, zum Beispiel Stickstoff, Kupfer oder Wasser. Diamagnetische Stoffe haben das Bestreben, das Magnetfeld aus ihrem Innern zu verdrängen. Sie magnetisieren sich gegen die Richtung eines externen Magnetfeldes, folglich ist μ_r < 1. Diamagnetische Beiträge sind im Allgemeinen temperaturunabhängig. Einen Sonderfall stellen die Supraleiter dar. Sie verhalten sich im konstanten Magnetfeld als ideale Diamagneten mit μ_r = 0. Dieser Effekt heißt Meißner-Ochsenfeld-Effekt und ist ein wichtiger Bestandteil der Supraleitung.

Paramagnetische Stoffe μ_r > 1

Für die meisten Materialien ist die Permeabilitätszahl etwas größer als Eins (zum Beispiel Sauerstoff, Luft) – die so genannten paramagnetischen Stoffe. In paramagnetischen Stoffen richten sich die atomaren magnetischen Momente in externen Magnetfeldern aus und verstärken damit das Magnetfeld im Innern des Stoffes. Die Magnetisierung ist also positiv und damit μ_r > 1. Die Temperaturabhängigkeit der Suszeptibilität wird durch das Curiesches Gesetz bestimmt. Paramagnetismus kann auch andere Ursachen haben, so liefern Leitungselektronen von Metallen einen temperaturunabhängigen Beitrag (Pauli-Paramagnetismus).

Ferromagnetische Stoffe $\mu_r \gg 1$

Besondere Bedeutung kommt den ferromagnetischen Stoffen bzw. den weichmagnetischen Werkstoffen (Eisen und Ferrite, Cobalt, Nickel) zu, da diese sehr große Permeabilitätszahlen von μ_r > 300 bis zu 300.000 aufweisen. Diese Stoffe kommen in der Elektrotechnik häufig zum Einsatz (Spule, Elektromotor, Transformator). Ferromagneten richten ihre magnetischen Momente parallel zum äußeren Magnetfeld aus, tun dies aber in einer stark verstärkenden Weise. Neben ferromagnetischen Stoffen weisen auch ferrimagnetische und antiferromagnetische Stoffe eine magnetische Ordnung auf.

Besonderheit der Permeabilität bei Materialien mit einer magnetischen Ordnung

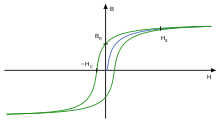
Die Magnetisierung bei ferromagnetischen Stoffen hängt im Allgemeinen nicht linear vom äußeren Magnetfeld ab. Es ist vielfach möglich, einen Ferromagneten komplett zu magnetisieren. Außerdem hängt die Magnetisierung von der vorhergehenden Magnetisierung ab, man sagt sie haben ein Gedächtnis. Das Verhalten wird durch eine Hystereseschleife beschrieben. Die einfache lineare Definition der Permeabilität ist also nicht immer anwendbar.

Je nach Anwendung werden verschiedene Definitionen der Permeabilität benutzt. Für technische Anwendungen ist sie in DIN 1324 Teil 2 insgesamt elf Mal mit unterschiedlichen Berechnungen definiert. Neben der Permeabilität μ als Quotient aus magnetischer Flussdichte B in Tesla (T) und magnetischer Feldstärke H in Ampere pro Meter (A/m) ist vor allem die differentielle Permeabilität, als Steigung der Hysteresekurve von Bedeutung.

Hysteresekurve

Eine Problematik bei der konstant angenommenen Permeabilität kann man anhand der Hysteresekurve sehen. Die Permeabilität μ entspricht der Steigung

$\mu=\frac{\mathrm{d}B}{\mathrm{d}H}$ bzw. bei magnetischer Anisotropie: $\mu_{ij}=\frac{\partial B_i}{\partial H_j}$.

Aufgrund der magnetischen Sättigung, sowie der magnetischen Remanenz, ist die Permeabilität nicht konstant. Für kleine Felder ist die Permeabilität deutlich größer als nahe der Sättigung.

Im allgemeinen (aber linearen) Fall ist die magnetische Permeabilität in Materie ein Tensor und beschreibt damit auch die Anisotropie des Materials. Nur im speziellen (vereinfachten) Fall, wenn Linearität und Isotropie gegeben ist, ist die Permeabilität eine skalare Materialkonstante.

Literatur

• Hans Fischer: Werkstoffe in der Elektrotechnik. Aufbau, Eigenschaften, Prüfung, Anwendung. 2. überarbeitete Auflage. Carl Hanser Verlag, München u. a. 1982, ISBN 3-446-13553-7.
• Horst Kuchling: Taschenbuch der Physik. 4. Auflage. Verlag Harri Deutsch, Thun u. a. 1982, ISBN 3-87144-097-3.
• Günter Springer: Fachkunde Elektrotechnik. 18. völlig neubearbeitete und erweiterte Auflage. Verlag Europa-Lehrmittel, Wuppertal 1989, ISBN 3-8085-3018-9 (Europa-Lehrmittel 30318).
• Horst Stöcker (Hrsg.): Taschenbuch der Physik. Formeln, Tabellen, Übersichten. 4. korrigierte Auflage. Verlag Harri Deutsch, Thun u. a. 2000, ISBN 3-8171-1628-4.
• Physikalisch-Technische Bundesanstalt (Hrsg.): Faltblatt: Die gesetzlichen Einheiten in Deutschland. (PDF-Datei, 84 kB).

Siehe auch

• Permittivität
• Faraday-Waage