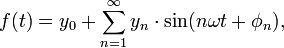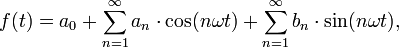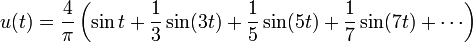Fourieranalyse

Die Fourier-Analyse beschreibt das Zerlegen eines beliebigen periodischen Signals in eine Summe von Sinus- und Kosinusfunktionen (eine Fourier-Reihe). Sie zerlegt ein Signal damit in seine Frequenzanteile. Die Fourier-Synthese hingegen beschreibt das umgekehrte Verfahren, die Erzeugung beliebiger Signale aus Sinus- und Kosinusfunktionen. Für eine ausführliche Diskussion der verschiedenen Verfahren ähnlichen Namens und eine mathematische Herleitung sei auf den Artikel zur Fourier-Transformation verwiesen.

Das dick gezeichnete Signal wird durch die Fourier-Analyse in die beiden dünn gezeichneten Signale zerlegt. Die positive und die negative Halbwelle sehen gleich aus, weil ein Anteil mit dreifacher Frequenz addiert wurde.

Hier sind positive und die negative Halbwelle unterschiedlich, weil ein Anteil mit doppelter Frequenz addiert wurde.

Funktionsweise

Sei 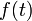$\ f(t)$ eine beliebige periodische Funktion, ihre Fourier-Zerlegung sieht dann wie folgt aus:

$\ f(t)= y_0 + \sum_{n=1}^\infty y_n \cdot \sin(n \omega t + \phi_n),$

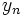wobei $\ y_n$ die Amplituden und 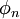$\ \phi_n$ die Phasen sind. Diese Funktion kann mit einem Additionstheorem zerlegt werden:

$\ f(t)= a_0 + \sum_{n=1}^\infty a_n \cdot \cos(n \omega t)+\sum_{n=1}^\infty b_n \cdot \sin(n \omega t),$

Die Aufgabe der Fourier-Analyse besteht in der Berechnung der Koeffizienten a_n und b_n mit Hilfe von Integralen über eine volle Periode.

Beispiel

Als Beispiel für die Funktionsweise soll die Zerlegung eines Rechtecksignals (Tastverhältnis 50%, kein Gleichspannungsanteil) dienen. Die Funktion lautet

$u(t) = \begin{cases} 1, & \mbox{ wenn } 0\leq \omega t <\pi \\ -1, & \mbox{ wenn } \pi \leq \omega t < 2\pi \end{cases} \qquad u(t + 2\pi / \omega) = u(t), \omega = 1 * 1/s \,$.

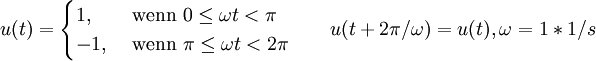Die Funktion ist demzufolge 2π-periodisch.

Entwickelte man die Beispielfunktion in eine Fourier-Reihe, so erhält man die folgende unendliche Reihe:

$u(t)=\frac{4}{\pi}\left(\sin t+\frac{1}{3}\sin(3 t)+\frac {1}{5}\sin(5 t)+\frac{1}{7}\sin(7 t)+ \cdots\right) \,$

Anhand dieser Funktion erkennt man, dass man eine Rechteckschwingung durch unendlich viele Harmonische darstellen kann. Sie enthält jeweils die ungeraden harmonischen Oberschwingungen, wobei die Amplitude mit steigender Frequenz abnimmt. Aufgrund dessen wird ein Rechtecksignal auch häufig zum Testen elektronischer Schaltungen genommen, da so das Frequenzverhalten dieser Schaltung erkannt wird.

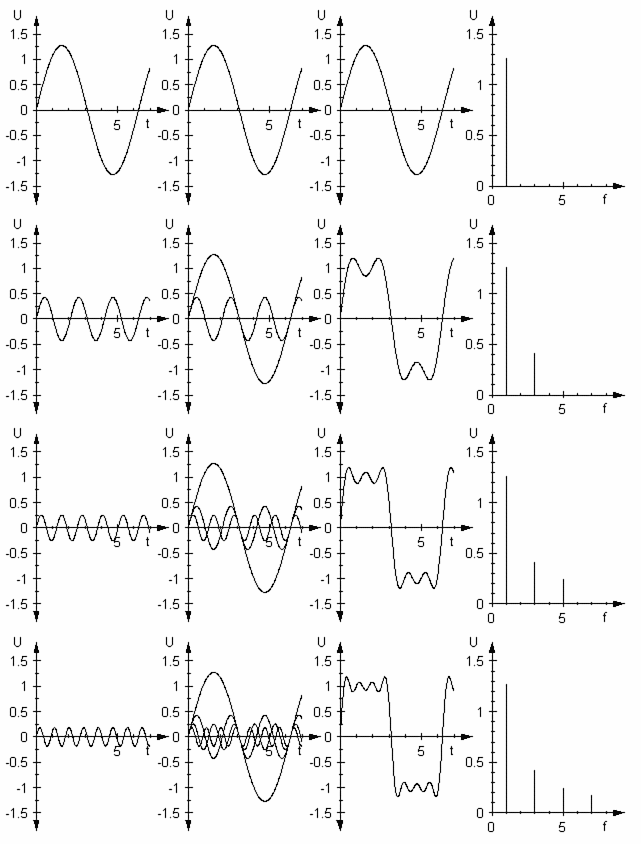
Im folgenden Bild ist die Fourier-Synthese eines Rechtecksignals dargestellt. Die Diagramme der ersten Spalte zeigen diejenige Schwingung, die in der jeweiligen Zeile hinzugefügt wird. Die Diagramme in der zweiten Spalte zeigen alle bisher berücksichtigten Schwingungen, die dann in den Diagrammen der dritten Spalte addiert werden, um dem zu erzeugenden Signal möglichst nahe zu kommen. Die Schwingung aus der ersten Zeile nennt sich Fundamentalschwingung, alle weiteren, die hinzugefügt werden, sind Oberschwingungen (Harmonische). Je mehr solcher Vielfache der Grundfrequenz berücksichtigt werden, umso näher kommt man einem idealen Rechtecksignal. An den unstetigen Stellen des Rechtecksignals bildet sich durch die Fourier-Synthese bedingt ein so genannter Überschwinger, der auch bei größerer Approximation nicht verschwindet. Diese Erscheinung wird Gibbssches Phänomen genannt, für eine große Anzahl an überlagerten Schwingungen macht sie etwa 9 % des vollen Sprungs aus. Die vierte Spalte zeigt zunächst das Amplitudenspektrum. Zu einem Frequenzspektrum wird es dann, wenn man die Anzahl der Abtastpunkte in Verbindung mit der Abtastfrequenz bringt.

Anwendungsbeispiel

Als Beispiel (mit Diskretheit): Eine Schwingung wird mit einer Frequenz von 44,1 kHz abgetastet. Nun wird mit den so erhaltenen Werten eine komplexwertige Diskrete Fourier-Transformation mit 512 Punkten durchgeführt. Man erhält das Amplitudenspektrum, das von 0 bis 512 läuft. Allerdings ist dabei folgendes zu beachten: Das eigentliche Amplitudenspektrum läuft nur von 0 bis 255. Ab 256 bis 512 ergibt sich eine Spiegelung desselben. Dieses hängt mit den "negativen Frequenzen" zusammen, die zwar z.B. physikalisch keine Rolle spielen, aber mathematisch. Bei der o. g. Abtastfrequenz ergibt sich nach dem Abtasttheorem eine Darstellung von 0 bis 22,05 kHz. Das bedeutet: 0 steht für > 0 Hz (da keine Gleichstromanteile vorhanden sind) und 254 steht für 22,05 kHz.

Siehe auch

• Ordnungsanalyse

Weblinks

• Fourier Series Applet Java-Applet zur Demonstration der Fourier-Synthese (englisch, benötigt Java).