- Fourierentwicklung
-
Als Fourierreihe (nach Jean Baptiste Joseph Fourier) einer periodischen Funktion f(x), die abschnittsweise stetig ist, bezeichnet man deren Entwicklung in eine Funktionenreihe aus Sinus- und Kosinusfunktionen.
Die Basisfunktionen der Fourierreihe bilden das bekannteste Beispiel für ein orthogonales Funktionensystem. Im Rahmen der Theorie der Hilberträume werden auch Entwicklungen nach einem beliebigen vollständigen Orthonormalsystem als Fourierreihe bezeichnet.
Inhaltsverzeichnis
Geschichte
Bereits im 18. Jahrhundert kannten Mathematiker wie Euler, Lagrange oder die Bernoullis Fourierreihen für einige Funktionen. Zu Beginn des 19. Jahrhundert behauptete nun Fourier in seinem Werk Théorie analytique de la chaleur, dass es für alle Funktionen solche Reihenentwicklungen gebe. Diese Behauptung stieß zunächst bei führenden Mathematikern wie Cauchy und Abel auf Ablehnung.
Dirichlet konnte 1829 beweisen, dass Fouriers Behauptung zumindest für Lipschitz-stetige Funktionen zutrifft. Du Bois-Reymond fand 1873 eine stetige Funktion, deren Fourierreihe divergiert. Im 20. Jahrhundert gelangte man schließlich zur Erkenntnis, dass es auch für stetige oder stückweise stetige Funktionen konvergente Fourierreihen gibt, wenn der Konvergenzbegriff geeignet abgeschwächt wird.
Darstellungsformen
Die Partialsummen einer Fourierreihe sind trigonometrische Polynome. Wie diese können Fourierreihen in drei gleichwertigen Formen dargestellt werden. Zu jeder dieser Darstellungen gibt es zugehörige Formeln zum Bestimmen der Koeffizienten bzw. Parameter der Fourierreihenentwicklung einer periodischen Funktion.
Eine Fourierreihenentwicklung einer periodischen Funktion f mit Periode T>0 ist in den folgenden, schrittweise allgemeiner werdenden Fällen möglich:
- wenn f stetig und abschnittsweise stetig differenzierbar ist; die Fourierreihe konvergiert dabei punktweise und gleichmäßig.
- wenn f eine beschränkte totale Variation über einer Periode hat, und die Funktionswerte von f mit dem Mittel aus den links- und rechtsseitigen Grenzwerten übereinstimmen,
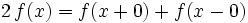 für alle
für alle 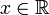 ; die Fourierreihe konvergiert dann nur punktweise.
; die Fourierreihe konvergiert dann nur punktweise. - wenn f, auf eine Periode [c,c + T] eingeschränkt, dem Funktionenraum L2([c,c + T]) angehört; mit Konvergenz im Sinne der L²–Norm.
Allgemeine Form
Eine periodische Funktion f mit Periode T>0, die einer der angegebenen Klassen angehört, lässt sich durch eine Reihe von Sinus- und Kosinusfunktionen darstellen, deren Frequenzen ganzzahlige Vielfache der Grundfrequenz ω = 2π / T sind,
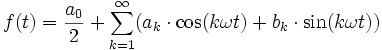 .
.
Die Kreisfrequenz ω skaliert hierbei die Periode 2π von Sinus und Kosinus auf die entsprechende Periode T. In der praktischen Anwendung wird man die Reihe häufig nach endlich vielen Reihengliedern abbrechen. Man erhält dann nur eine Approximation von f in Form eines trigonometrischen Polynoms.,
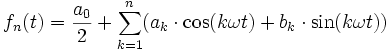 .
.
Diese endliche Summe wird dann Teilsumme fn(t) der Fourierreihe genannt. Das so entstehende trigonometrische Polynom ist, unter allen trigonometrischen Polynomen der gleichen Struktur, dasjenige mit minimalem mittleren quadratischen Fehler zur ursprünglichen Funktion f.
Die Koeffizienten der Entwicklung von f sind
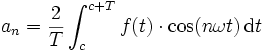 und
und 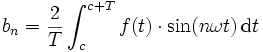
Das c stellt eine Verschiebung des Intervalls dar und kann zur Vereinfachung beliebig gewählt werden.
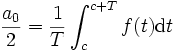 ist der Gleichanteil (wechsellose Größe)
ist der Gleichanteil (wechsellose Größe)
Einfache Eigenschaften dieser Entwicklung sind, dass
- bn = 0 für alle n gilt, falls f gerade ist, f( − x) = f(x)
- an = 0 für alle n gilt, falls f ungerade ist, f( − x) = − f(x)
Sind alle bn = 0, d.h. ist f gerade, so kann an auch über
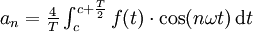 berechnet werden. Dies ist möglich, weil durch die Symmetrie des Kosinus und der Funktion die Werte des Integrals in beiden Halbintervallen gleich sind. So ergeben sich oft Vereinfachungen. Umgekehrt gilt dies auch für an = 0.
berechnet werden. Dies ist möglich, weil durch die Symmetrie des Kosinus und der Funktion die Werte des Integrals in beiden Halbintervallen gleich sind. So ergeben sich oft Vereinfachungen. Umgekehrt gilt dies auch für an = 0.Ist die zugrundeliegende Funktion unbekannt bzw. liegen nur gegebene diskrete Daten (z. B. Messwerte) vor, werden an, bn nur aus den Stützpunkten approximiert (Trigonometrische Interpolation).
Amplituden-Phasen-Notation
In der obigen Darstellung wird das Signal mit Hilfe eines Sinusspektrums und eines Kosinusspektrums dargestellt. Es ist aber auch eine Darstellung mittels Phasen- und Amplitudenspektrums möglich, da man die additive Überlagerung (Interferenz) einer Sinus- und einer Kosinusschwingung auch als phasenverschobene Kosinusschwingung darstellen kann:
Dabei ist
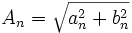 und
und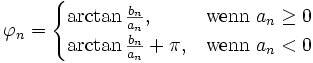
bzw.
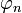 zeigt in den Quadranten, in welchem auch der Punkt (an,bn) liegt.
zeigt in den Quadranten, in welchem auch der Punkt (an,bn) liegt.Komplexe Fourierreihe
Man kann nun jedes Paar von Amplitude und Verschiebung als komplexe Zahl in Polarkoordinatendarstellung interpretieren. Damit lassen sich die beiden Spektren in eines überführen. Eine Vereinfachung von geraden bzw. ungeraden Funktionen wie im Reellen ist so jedoch nicht möglich.
Dabei ist
Die Berechnung ist oft einfacher, da zum einen die e-Funktion leicht zu integrieren ist und zum anderen nur noch ein Koeffizient statt zwei zu berechnen ist.
Zusammenhang zwischen reellen und komplexen Fourierkoeffizienten
Reell zu komplex:
Komplex zu reell:
Beispiele
Dreieckpuls
Die Dreieckfunktion lässt sich je nach gewünschter Phasenlage mit Sinus- und Kosinustermen approximieren. Mit h kann man die Amplitude der Kurve bestimmen:
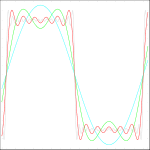
Rechteckpuls
Gleiches gilt für den Rechteckpuls:
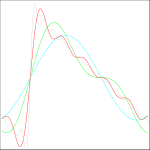
Sägezahnpuls (steigend)
Ebenso lassen sich punktsymmetrische Funktionen aus Sinustermen approximieren. Hier erreicht man eine Phasenverschiebung durch alternierende Vorzeichen:
Sinuspuls
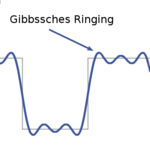
Gibbssches Phänomen
- Hauptartikel: Gibbssches Phänomen
In der Umgebung von Sprungstellen entstehen bei der Fourierreihe typische Über- und Unterschwinger von etwa 18% der Sprunghöhe, da dort die Reihe nicht mehr gleichmäßig, sondern nur noch punktweise konvergiert. Dieser Effekt hat weitreichende Auswirkungen in der Signalverarbeitung.
- Siehe auch: Diskrete Fourier-Transformation
Weblinks
- Falstad Fourier Series Java Applet Mit diesem Java-Applet kann man sich zeigen lassen, wie Fourier-Reihen entwickelt werden.
- Mathe-Online Fourier Applet Weiteres Applet zur Entwicklung von Fourier-Reihen.
- Bernhard Riemann: Ueber die Darstellbarkeit einer Function durch eine trigonometrische Reihe
- Spektren periodischer Zeitfunktionen (PDF) Fourier-Zerlegung physikalisch mit Hilfe einer graphischen Veranschaulichung betrachtet.
Siehe auch
Wikimedia Foundation.

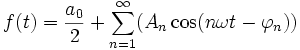

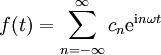
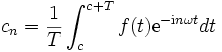
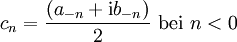
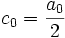
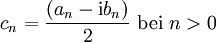
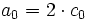
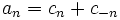

![\begin{array}{rl}
f(t)
=& -\frac{8h}{\pi^2}\left[ {\cos{\omega t} + \frac{1}{3^2} \cos{3 \omega t} + \frac{1}{5^2} \cos{5 \omega t} + \cdots}\right] \\[.6em]
=& -\frac{8h}{\pi^2} \sum_{k=1}^\infty \dfrac{ \cos ((2k-1) \omega t)}{(2k-1)^2}
\end{array}](/pictures/dewiki/57/9fdb961758d5fe561f389709b77d3158.png)
![\begin{array}{rl}
f(t)
=& \frac{8h}{\pi^2}\left[ {\sin {\omega t} - \frac {1}{3^2}\sin{3 \omega t} + \frac {1}{5^2}\sin {5 \omega t} \mp \cdots}\right] \\[.6em]
=& \frac {8h}{\pi^2} \sum_{k=1}^\infty (-1)^{k-1} \dfrac{ \sin((2k-1) \omega t)}{(2k-1)^2}
\end{array}](/pictures/dewiki/54/6164f6941c2ba1ffa2dfa57a6bcafc51.png)
![\begin{array}{rl}
f(t)
=& \frac{4h}{\pi}\left[ {\sin {\omega t} + \frac {1}{3}\sin{3 \omega t} + \frac {1}{5}\sin{5 \omega t} + \cdots}\right] \\[.6em]
=& \frac{4h}{\pi} \sum_{k=1}^\infty \dfrac{ \sin\left( (2k-1)\omega t \right) }{2k-1}
\end{array}](/pictures/dewiki/98/bf73438a4a56c2aa846a4e951073ab9e.png)
![\begin{array}{rl}
f(t)
=& \frac{4h}{\pi}\left[ {\cos {\omega t} - \frac {1}{3}\cos{3 \omega t} + \frac {1}{5}\cos{5 \omega t} \mp \ldots}\right] \\[.6em]
=& \frac{4h}{\pi} \sum_{k=1}^\infty (-1)^{k-1} \dfrac{\cos\left( (2k-1)\omega t \right)}{ 2k-1}
\end{array}](/pictures/dewiki/97/ab3a4de83ed57028f2954a428674cf58.png)
![\begin{array}{rl}
f(t)
=&- \frac{2h}{\pi}\left[ {\sin {\omega t} - \frac {1}{2}\sin{2 \omega t} + \frac {1}{3}\sin {3 \omega t} \mp \cdots}\right] \\[.6em]
=& - \frac {2h}{\pi}\sum_{k=1}^{\infty}(-1)^{k-1} \dfrac {\sin k \omega t}{k}
\end{array}](/pictures/dewiki/55/7042fbdf394af4f2c38b6dfe1213547c.png)

![\begin{array}{rl}
f(t)
=& h\left| \sin {\omega t} \right|\\[.6em]
=& \frac{4h}{\pi}\left[ \frac{1}{2} - \frac { \cos {2 \omega t}}{3}-\frac { \cos {4 \omega t}}{15}-\frac { \cos {6 \omega t}}{35}- \cdots\right] \\[.6em]
=& \frac{2h}{\pi} - \frac{4h}{\pi} \sum_{k=1}^{\infin} \dfrac { \cos {2 k\omega t}}{(2k)^2-1}
\end{array}](/pictures/dewiki/100/d8f53e0174173a070c01c87096b5a788.png)