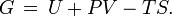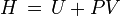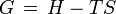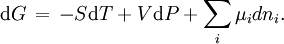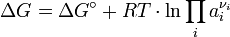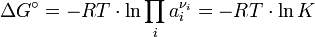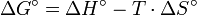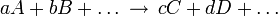Freie Reaktionsenthalpie

Die Gibbs-Energie G, benannt nach dem US-amerikanischen Physiker Josiah Willard Gibbs, ist ein thermodynamisches Potential mit den natürlichen unabhängigen Variablen Temperatur T, Druck P und Stoffmenge n. Im deutschen Sprachraum wird die Gibbs-Energie meist als Freie Enthalpie bezeichnet; gebräuchlich sind auch Gibbssche freie Energie oder Gibbs-Potential. Diese Bezeichnungen sollen in der Chemie jedoch nach einer Empfehlung der IUPAC nicht mehr verwendet werden ^[1].

Die Gibbs-Energie ist definiert durch

$G \,=\, U + P V - T S.$

Da

$H \,=\, U + P V$

ist, gilt

$G \,=\, H - T S$

mit der inneren Energie U, dem Volumen V, der Entropie S sowie der Enthalpie H. Im Gleichgewicht ist der differentielle Ausdruck davon

$\mathrm{d}G \,=\, -S \mathrm{d}T + V \mathrm{d}P + \sum_{i} \mu_{i} dn_{i}.$

mit dem chemischen Potential µ_i. Diese Gleichung ist maßgeblich für chemische Reaktionen, da diese sehr häufig an ein Druck- sowie an ein Temperatur-Reservoir gekoppelt sind.

Die Einheit der Gibbs-Energie ist Joule/mol (J/mol).

Geschichtliches

Die Arbeiten von Josiah Willard Gibbs zur Thermodynamik erschienen zunächst nur in den relativ schwer zugänglichen „Transactions of the Connecticut Academy“. Der Chemiker Wilhelm Ostwald befasste sich eingehend mit der Bedeutung dieser Arbeiten und schrieb an Gibbs: „Die Bedeutung Ihrer Arbeit ist eine so große, dass ich soviel ich kann, dazu tun möchte, ihr eine entsprechende Verbreitung zu schaffen“. Im Jahr 1892 erschien das von Ostwald verfasste Buch „Thermodynamischen Studien“ auf Basis der Arbeit von Gibbs. Zuvor hatte der aus Potsdam gebürtige Hermann Helmholtz drei größere Abhandlungen über die „Thermodynamik chemischer Vorgänge“ (1882/83, s. Helmholtz-Energie) geschrieben. Dabei übertrug Helmholtz die Hauptsätze der Thermodynamik auf den Galvanismus und auf elektrochemische Vorgänge. Mit der von Ostwald und van ’t Hoff begründeten „Zeitschrift für physikalische Chemie, Stöchiometrie und Verwandtschaftslehre“ wurde die physikalische Chemie zu einer eigenständigen Wissenschaftsdisziplin. Gibbs Arbeit war in dieser neuen physikalischen Chemie ein Grundpfeiler. Der Assistent von Ostwald, Walther Nernst, entwickelte bei Ostwald die „osmotische Theorie der galvanischen Elemente“; der Kern dieser Abhandlung ist heute besser als die „Nernst-Gleichung“ bekannt. Die Gibbsschen Gesetze ließen sich so auch in abgeleiteter Form mit der Elektrochemie vereinbaren.

Anwendung der Gibbs-Energie in der Chemie

Chemische Reaktionen gehorchen den Gesetzen der Thermodynamik. Die Thermodynamik beschreibt Beziehungen zwischen verschiedenen Energieformen und beantwortet die Frage, ob, unter welchen Bedingungen und in welchem Umfang eine Umsetzung der beteiligten Stoffe abläuft. Hier ist das entscheidende Kriterium die Gibbs-Energie G. Für ihre Änderung ΔG während einer Reaktion gilt

• ΔG < 0: exergone Reaktion, die unter den gegebenen Bedingungen (Konzentrationen) spontan abläuft;
• ΔG = 0: Gleichgewichtssituation, keine Reaktion;
• ΔG > 0: endergone Reaktion, deren Ablauf in der angegebenen Richtung Energiezufuhr erfordern würde.

Für die Änderung der Gibbs-Energie gilt nun:

$\Delta G = \Delta G^{\circ} + R T \cdot \ln \prod_{i} a_{i}^{\nu_{i}}$

Darin ist a die Aktivität des entsprechenden Reaktanden. R steht für die universelle Gaskonstante:

• $R = 8{,}314471(15)\ \mathrm{J\ mol^{-1}K^{-1}}$
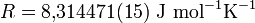
• T ist die absolute Temperatur in Kelvin
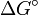• $\Delta G^{\circ}$ eine reaktionsspezifische Konstante, die freie Standardenthalpie. (Obacht! 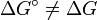$\Delta G^{\circ} \neq \Delta G$ vgl. Standardzustand.)

Es gilt die Gleichheit 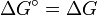$\Delta G^{\circ}= \Delta G$, wenn alle Edukte und Produkte die Aktivität 1 besitzen und somit 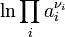$\ln \prod_{i} a_{i}^{\nu_{i}}$ gleich Null wird. Aufgrund des Vorzeichens kann aus 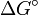$\Delta G^{\circ}$ also die (hypothetische) Reaktionsrichtung bei a = 1 für alle Reaktionspartner abgelesen werden (sog. „Standardbedingungen“). In der Biochemie wird das 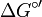$\Delta G^{\circ\prime}$ verwendet, um die Gibbs-Energie bei physiologischem pH 7 zu kennzeichnen.

Die Gleichgewichtseinstellung der Reaktion folgt dem Kriterium minimaler Gibbs-Energie. Im Gleichgewicht ändert sich G definitionsgemäß nicht mehr, d. h. es gilt ΔG = 0, woraus folgt:

$\Delta G^{\circ} = -R T \cdot \ln \prod_{i} a_{i}^{\nu_{i}} = -R T \cdot \ln K$

Hierbei ist K die Thermodynamische Gleichgewichtskonstante.

Auf der anderen Seite ist ΔG mit den Aktivitäten der Reaktionspartner veränderlich. 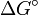$\Delta G^{\circ}$ ist derjenige Wert, welcher die Reaktionsrichtung bestimmt: Nur bei negativem 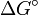$\Delta G^{\circ}$ liegt die Reaktionsrichtung auf der Produktseite. Eine durch positives 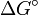$\Delta G^{\circ}$ gekennzeichnete Reaktion kann durchaus in der geschriebenen Richtung ablaufen, sofern die Ausgangsaktivitäten ein negatives ΔG gewährleisten.

Interessiert nur die Temperaturabhängigkeit einer chemischen Reaktion, so wird oft vereinfacht die Gleichung

$\Delta G^{\circ} = \Delta H^{\circ} - T \cdot \Delta S^{\circ}$

benutzt. Diese Gleichung erlaubt allerdings nur eine Aussage darüber, ob eine chemische Reaktion in der gegebenen Richtung freiwillig ablaufen kann. Mitunter sind Reaktionen sogar selbst unter Katalysatoreinfluss gehemmt (beispielsweise die Ammoniakbildung aus Wasserstoff und Stickstoff). Aussagen über die Reaktionsgeschwindigkeit sind somit nicht möglich.

Es sei folgende allgemeine chemische Reaktion gegeben:

$a A + b B + \dots \, \rightarrow \, c C + d D + \dots$

Dabei sind a, b, c, d sind die stöchiometrischen Faktoren und A, B, C, D sind die chemischen Verbindungen oder Elemente.

Aus dieser allgemeinen chemischen Reaktion lässt sich bei Kenntnis der freien Bildungsenthalpien im Standardzustand von Verbindungen (werden mit (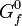$G_f^0$) angegeben – im unteren Beispiel zur Unterscheidung jedoch mit (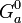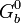$G_a^0$), ($G_b^0$) – und beziehen sich immer auf 1 mol der entsprechenden Verbindung) die freie Enthalpie (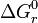$\Delta G_r^0$) einer chemischen Umsetzung berechnen.

Für die Berechnung gilt:

$\mathrm{(I)} \quad \Delta G_r^0 = c G_c^0 + d G_d^0 + \, \dots \, - a G_a^0 - b G_b^0 + \dots$

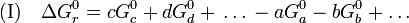
Eine chemische Reaktion ist – wie oben beschrieben – nur möglich, wenn 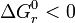$\Delta G_r^0 &amp;lt; 0$ ist.

Zur Untersuchung von speziellen thermodynamischen Problemstellungen kann die freie Enthalpie der Gibbs-Gleichung differenziert und anschließend integriert werden. Folgende thermodynamische Problemstellungen sind besonders wichtig:

Die Druckabhängigkeit bei der Reaktion von idealen Gasen:

$\mathrm{(II)} \quad \Delta G_r = c G_c^0 + d G_d^0 + \, \dots \, - a G_a^0 - b G_b^0 + \, \dots + RT \, \ln \frac{(p_c) \cdot (p_d) \cdot \,\dots}{(p_a) \cdot (p_b) \cdot \, \dots}$

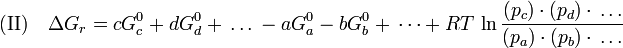
(p_c , p_d, p_a , p_b sind die Partialdrucke des jeweiligen Gases.)

Analoges gilt für Lösungen:

$\mathrm{(III)} \quad \Delta G_r = cG_c^0 + dG_d^0 + \, \dots \, - aG_a^0 - bG_b^0 + \, \dots \, + RT \, \ln(K)$

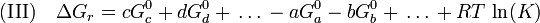
(K entspricht dem obigen Term wobei die Partialdrucke jedoch durch die molaren Konzentrationen ausgetauscht werden müssen)

Falls sich die Reaktion im Gleichgewicht – d. h. ΔG_r = 0 – befindet, erhält man das oben beschriebene Massenwirkungsgesetz:

$\mathrm{(IV)} \quad \Delta G_r^0 = - RT \, \ln(K)$

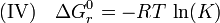
Die Temperaturabhängigkeit der Gibbs-Gleichung ergibt nach Bildung des Differentials und Integration die sogenannte van ’t Hoffsche Gleichung (RGT-Regel).

In der Elektrochemie (s. Elektrochemische Spannungsreihe) kann die geleistete Nutzarbeit einer freiwilligen Umwandlung von chemischen Stoffen (z. B. einer Brennstoffzelle) über die Beziehung:

$\mathrm{(V)} \quad \Delta G_r = -n \cdot F \cdot \Delta E$

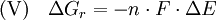
(n: Mol Elektronen, F: Faradaykonstante: 96480 As/mol, ΔE: Zellspannung, Einheit: As · V = J) bestimmt werden.

Siehe auch

• Aktivität
• Gibbs-Helmholtz-Gleichung
• Gruppenübertragungspotential
• Massenwirkungsgesetz
• Redox-Potential
• Thermodynamisches Potential

Literatur

• Lothar Dunsch: Das Portrait: Wilhelm Ostwald. In: Chemie in unserer Zeit, 16. Jahrgang, Dezember 1982, S. 186–196. Verlag Chemie.
• Wolfgang U. Eckart und Christoph Gradmann: Hermann Helmholtz und die Wissenschaft im 19. Jahrhundert. In: Spektrum der Wissenschaften, Dezember 1994, S. 100–109.
• Hans Rudolf Christen: Grundlagen der allgemeinen und anorganischen Chemie. 5. Auflage, 1977, S. 291–313 Verlag Sauerländer AG.
• Handbook of Chemistry and Physics, CRC-Press, Florida 1981.

Einzelnachweise

1. ↑ IUPAC Compendium of Chemical Terminology, Gibbs energy

Weblinks

• IUPAC-Definition
• Bioenergetik