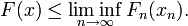Gamma-Konvergenz

In der Variationsrechnung bezeichnet Γ-Konvergenz (Gamma-Konvergenz) eine spezielle Konvergenzart für Funktionale. Sie wurde von Ennio de Giorgi eingeführt.

Definition

Sei X ein topologischer Raum und (F_n) eine Folge von Funktionalen $F_n: X \rightarrow [0, \infty]$ auf X. Die Folge (F_n) konvergiert im Sinne der Γ-Konvergenz gegen den Γ-Grenzwert $F: X \rightarrow [0,\infty]$, falls die folgenden zwei Bedingungen gelten:

• Für jede konvergente Folge (x_n) in X mit Grenzwert $x \in X$ gilt

$F(x)\le\liminf_{n\to\infty} F_n(x_n).$

• Zu jedem $x \in X$ gibt es eine Folge (x_n) in X, die gegen x konvergiert und

$F(x)\ge\limsup_{n\to\infty} F_n(x_n)$

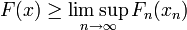
erfüllt.

Die erste Bedingung bedeutet, dass F eine „gemeinsame asymptotische untere Schranke“ für die F_n ist; die letztere Bedingung hingegen garantiert die Optimalität.

Eigenschaften

• Minimierer konvergieren gegen Minimierer: Eine Folge (x_n) heißt Minimalfolge für (F_n), falls

$\lim_{n\rightarrow\infty}\left(F_n(x_n) - \inf\{F_n(y)\ |\ y \in X\}\right) = 0$.

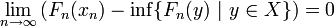Falls nun (F_n) gegen F Γ-konvergiert und (x_n) eine Minimalfolge für (F_n) ist, so ist jeder Häufungspunkt x von (x_n) ein Minimierer von F, d. h.

$F(x) = \inf\{F(y)\ |\ y \in X\}$.

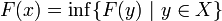• Γ-Grenzwerte sind stets unterhalbstetig.
• Γ-Konvergenz ist stabil unter stetiger Störung: Falls (F_n) gegen F Γ-konvergiert und $G: X \rightarrow [0, \infty]$ stetig ist, dann ist (F_n + g) Γ-konvergent gegen F + G.
• Eine konstante Folge von Funktionalen 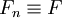$F_n \equiv F$ muss nicht notwendigerweise gegen F Γ-konvergieren, sondern gegen die Relaxation von F, nämlich das kleinste unterhalbstetige Funktional unterhalb von F.

Anwendungen

Eine wichtige Anwendung findet die Γ-Konvergenz in der Homogenisierungstheorie. Sie kann auch benutzt werden, um eine rigorose Begründung für den Übergang von diskreten zu kontinuierlichen Modellen zu liefern, beispielsweise bei der Elasitizitätstheorie.

Literatur

• Andrea Braides: Γ-convergence for Beginners. In: Oxford Lecture Series in Mathematics and Its Applications. Band 22, Oxford University Press, 2002, ISBN 0-19-850784-4.
• Gianni Dal Maso: An Introduction to Γ-Convergence. In: Progress in Nonlinear Differential Equations and Their Applications. Band 8, Birkhäuser, Basel 1993, ISBN 978-0-8176-3679-1.