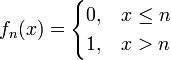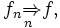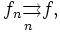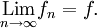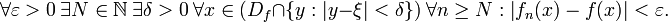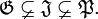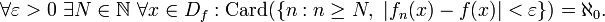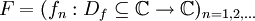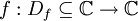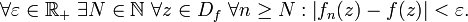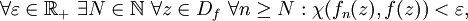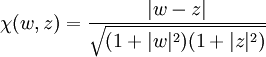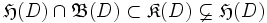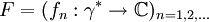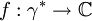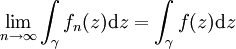- Chordal gleichmäßige Konvergenz
-
In der Analysis beschreibt gleichmäßige Konvergenz die Eigenschaft einer Funktionenfolge fn, mit einer vom Funktionsargument unabhängigen „Geschwindigkeit“ gegen eine Grenzfunktion f zu konvergieren. Im Gegensatz zu punktweiser Konvergenz erlaubt der Begriff der gleichmäßigen Konvergenz, wichtige Eigenschaften der Funktionen fn wie Stetigkeit, Differenzierbarkeit und Riemann-Integrierbarkeit, auf die Grenzfunktion f zu übertragen.
Inhaltsverzeichnis
Definition
Gegeben seien eine Funktionenfolge
die jeder natürlichen Zahl n eine reellwertige Funktion zuordnet, und eine Funktion f. Alle fn sowie f seien auf derselben Definitionsmenge Df definiert. Die Folge fn konvergiert gleichmäßig gegen f genau dann, wenn
Man betrachtet hier die absolute Differenz von
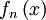 und
und 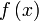 für alle x aus dem Definitionsbereich. Die Menge dieser Differenzen ist entweder unbeschränkt oder hat eine kleinste obere Schranke, ein Supremum. Gleichmäßige Konvergenz von fn gegen f bedeutet, dass dieses Supremum für fast alle n existiert und gegen Null geht, wenn n gegen unendlich strebt.
für alle x aus dem Definitionsbereich. Die Menge dieser Differenzen ist entweder unbeschränkt oder hat eine kleinste obere Schranke, ein Supremum. Gleichmäßige Konvergenz von fn gegen f bedeutet, dass dieses Supremum für fast alle n existiert und gegen Null geht, wenn n gegen unendlich strebt.Man kann diesen Sachverhalt auch anders definieren: Alle Bezeichnungen seien wie oben. Dann konvergiert fn gleichmäßig gegen f genau dann, wenn für alle
 ein
ein 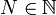 existiert, so dass für alle
existiert, so dass für alle 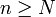 und für alle
und für alle 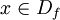 gilt:
gilt:Beispiel
Die Funktionenfolge
konvergiert auf ihrem Definitionsbereich für
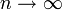 gleichmäßig gegen
gleichmäßig gegenVergleich zwischen gleichmäßiger und punktweiser Konvergenz
Die Wahl von N bei gleichmäßiger Konvergenz hängt nur von ε ab. Im Gegensatz dazu hängt bei punktweiser Konvergenz N sowohl von ε als auch von x ab, für diese schwächere Form von Konvergenz gilt:
- Für alle
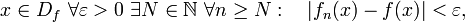
d. h., für punktweise Konvergenz muss es für jedes x und für jedes ε > 0 eine natürliche Zahl N geben, so dass für alle
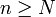 gilt:
gilt: 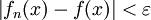 .
.Aus der gleichmäßigen Konvergenz folgt die punktweise Konvergenz, aber nicht umgekehrt. Beispielsweise konvergiert die Funktionenfolge
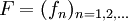 definiert durch
definiert durchpunktweise gegen f mit
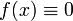 für jedes
für jedes 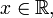 ist aber keine gleichmäßig konvergente Folge.
ist aber keine gleichmäßig konvergente Folge.Bezeichnung
Für die gleichmäßige Konvergenz einer Funktionenfolge
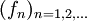 , die gegen f strebt, wird meistens eine der folgenden Bezeichnungen verwendet[1][2]
, die gegen f strebt, wird meistens eine der folgenden Bezeichnungen verwendet[1][2]oder
oder
Gleichmäßige Konvergenz in einem Punkt
Die Funktionenfolge ( fn )n=1,2,… heißt in dem Punkt ξ gegen f gleichmäßig konvergent, wenn
Wenn statt für alle n die Gültigkeit der Ungleichung | fn(x) − f(x) | < ε für mindestens ein n verlangt wird, dann heißt die Konvergenz uniform. Gleichmäßig konvergente Folgen sind auch uniform konvergent. Die uniforme Konvergenz impliziert keine punktweise Konvergenz.[3]
Sei
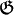 die Klasse der gleichmäßig konvergenten Funktionenfolgen,
die Klasse der gleichmäßig konvergenten Funktionenfolgen,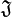 die Klasse der in jedem Punkt gleichmäßig konvergenten Funktionenfolgen und
die Klasse der in jedem Punkt gleichmäßig konvergenten Funktionenfolgen und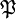 die Klasse der in jedem Punkt punktweise konvergenten Funktionenfolgen.
die Klasse der in jedem Punkt punktweise konvergenten Funktionenfolgen.
Es gilt
Die oben erwähnte Funktionenfolge
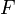 liegt in
liegt in 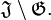
Einfach-gleichmäßige Konvergenz
Die Funktionenfolge ( fn )n=1,2,… heißt gegen f einfach-gleichmäßig konvergent, wenn
Jede gleichmäßig konvergente Funktionenfolge ist auch einfach-gleichmäßig konvergent.
Folgerungen
Wie schon erwähnt, ermöglicht der Begriff der gleichmäßigen Konvergenz ausgehend von Eigenschaften der Folge Aussagen über die Grenzfunktion, was bei punktweiser Konvergenz nicht möglich ist. Im Folgenden seien die Bezeichnungen wie bei der Definition oben, I sei ein reelles Intervall. Es ergeben sich folgende Sätze:
Stetigkeit
- Es sei fn eine Folge stetiger Funktionen. Wenn fn gleichmäßig gegen f konvergiert, dann ist f stetig.[4]
- Sei F = ( fn )n=1,2,… eine gegen f punktweise konvergente Funktionenfolge. Alle fn seien noch dazu in ξ stetig. f ist in ξ stetig genau dann, wenn F in dem Punkt ξ uniform konvergent ist.[3]
- Die Menge der Punkte gleichmäßiger Konvergenz sowie die Menge der Punkte uniformer Konvergenz einer überall punktweise konvergenten Funktionenfolge ist Gδ-Menge.[3]
- Die gleichmäßig konvergenten Funktionenfolgen mit kompaktem Definitionsbereich sind alle gleichgradig stetig.[1]
- Sei I ein kompaktes Intervall und F = ( fn ){ n=1,2,…} eine auf I gleichgradig stetige Folge. Wenn F punktweise gegen f konvergiert, dann konvergiert sie auch gleichmäßig.
- Sei F = ( fn )n=1,2,… eine Funktionenfolge mit kompaktem Definitionsbereich D. F besitzt eine gleichmäßig konvergenten Teilfolge genau dann, wenn sie F gleichgradig stetig ist und in jedem Punkt von D beschränkt ist (Satz von Arzelà-Ascoli).[1]
Differenzierbarkeit
- Für die Differenzierbarkeit der Grenzfunktion ergibt sich kein derart starkes Resultat wie für die Stetigkeit. Es seien die fn differenzierbar auf I und gleichmäßig konvergent gegen f. Im Allgemeinen braucht die Grenzfunktion nicht einmal differenzierbar sein, und wenn sie es ist, muss ihre Ableitung keineswegs gleich dem Grenzwert der Ableitungen der Folge sein. So konvergiert z. B. die durch fn(x) = sin(nx) / n definierte Funktionenfolge gleichmäßig gegen 0, die Folge der Ableitungsfunktionen fn aber nicht.
- Allgemein kann man sagen: Es seien alle fn differenzierbar. Wenn fn punktweise gegen f und die Ableitungen fn' gleichmäßig gegen g konvergieren, dann ist f differenzierbar mit der Ableitung g.
Integrierbarkeit
Für das Riemann-Integral auf Intervallen kommutieren bei gleichmäßiger Konvergenz Integration und Grenzwertbildung:
- Es seien alle fn (Riemann-)integrierbar. Wenn fn gleichmäßig gegen f konvergiert, dann ist f Riemann-integrierbar, und das Integral von f ist der Grenzwert der Integrale von fn.
Satz von Dini
- Wenn I ein kompaktes Intervall und fn eine monotone Folge stetiger Funktionen ist (d. h. fn + 1(x) ≥ fn(x) oder fn + 1(x) ≤ fn(x) für jedes n und beliebiges x), die punktweise gegen eine ebenfalls stetige Funktion f konvergiert, dann konvergiert fn auch gleichmäßig.
Gleichmäßige Konvergenz im Komplexen
Die gleichmäßige Konvergenz für komplexwertige Funktionenfolgen kann genau so wie im Falle von reellwertigen Funktionenfolgen definiert werden. Eine Funktionenfolge
heißt gegen
gleichmäßig konvergent, wenn
F heißt chordal gleichmäßig konvergent, wenn
wobei
die Bezeichnung für chordalen Abstand ist.
Sei
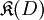 die Klasse der auf D gleichmäßig konvergenten Funktionenfolgen,
die Klasse der auf D gleichmäßig konvergenten Funktionenfolgen,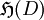 die Klasse der auf D chordal gleichmäßig konvergenten Funktionenfolgen und
die Klasse der auf D chordal gleichmäßig konvergenten Funktionenfolgen und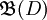 die Klasse der auf D gegen eine in D beschränkte Funktion punktweise konvergenten Funktionenfolgen.
die Klasse der auf D gegen eine in D beschränkte Funktion punktweise konvergenten Funktionenfolgen.
Es gilt
Grenzübergang unter dem Integralzeichen
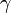 sei eine rektifizierbare Kurve. Die Elementen der Funktionenfolge
sei eine rektifizierbare Kurve. Die Elementen der Funktionenfolgeseien alle stetig. Wenn F gegen
gleichmäßig konvergiert, dann gilt für den Grenzübergang unter dem Integralzeichen
Siehe auch
- Kompakte Konvergenz
- Fast gleichmäßige Konvergenz
- Hierarchische Ordnung der Konvergenzbegriffe in Räumen mit endlichem Maß
- Kriterium für gleichmäßige Konvergenz von Abel
Quellen und Bemerkungen
- ↑ a b c Heuser H., Lehrbuch der Analysis, B.G.Teubner, Stuttgart, 1984, ISBN 3-519-22221-3, Teil 1, XIII., 103., 106.
- ↑ Zorich, V., Analysis II, Springer, 2007, ISBN 978-3-540-46231-6
- ↑ a b c Hausdorff F., Grundzüge der Mengenlehre, 1914, Chelsea Publishing Co., New York, 1949, Kap. IX, § 4.
- ↑ Hier ist die gleichmäßige Konvergenz nicht notwendig. Ausreichend ist auch die einfach-gleichmäßige Konvergenz.
Weblinks
- Uniform convergence in der Encyclopedia of Mathematics von Springer
- Eric W. Weisstein: uniform convergence auf MathWorld (englisch)
- gleichmäßige Konvergenz (Vorlesung Uni Saarbrücken)
Wikimedia Foundation.

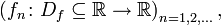
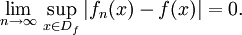
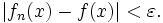
![\left(f_n\colon \left(0,\frac{1}{2}\right]\to\mathbb{R}\right)_{n=1,2,\ldots}\ \text{mit}\ f_n(x)=x^n](/pictures/dewiki/50/22d22447e8b6a544e24d3b65dfc54337.png)
![f\colon \left(0,\frac{1}{2}\right]\to\mathbb{R}\ \text{mit}\ f(x)=0](/pictures/dewiki/98/bb4a64dbf34bcfdc4259a25a9dc825c2.png)