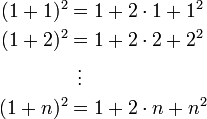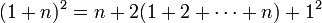Gaußsche Summierungsregel

Die gaußsche Summenformel, auch kleiner Gauß genannt, ist eine Formel für die Summe der ersten n aufeinander folgenden natürlichen Zahlen, also $1+2+3+4+\dots+n$.

$\sum_{i=1}^n i = \frac{n(n+1)}2$:

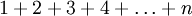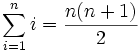Diese Reihe ist ein Spezialfall der arithmetischen Reihe und ihre Summen 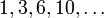$1,3,6,10,\dots$ werden auch Dreieckszahlen genannt.

Veranschaulichung

Man kann die Formel folgendermaßen veranschaulichen: Man schreibt die Zahlen von 1 bis n aufsteigend in eine Zeile. Darunter schreibt man die Zahlen in umgekehrter Reihenfolge (im Beispiel n = 11).

 1   2  3  4  5  6  7  8  9  10 11
11  10  9  8  7  6  5  4  3   2  1

Es ist gut zu erkennen, dass die Summe der Spalten im Beispiel jeweils den Wert 12 ergibt. Allgemein ergibt sich ein Wert von n + 1. Da es n Spalten sind, ist die Summe der Zahlen beider Zeilen gleich 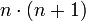$n \cdot (n+1)$. Um die Summe der Zahlen einer Zeile zu ermitteln wird das Ergebnis halbiert und es ergibt sich die obige Formel:

$\tfrac12\cdot n\cdot (n+1)$.

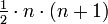Herkunft der Bezeichnung

Diese Summenformel ist die einfachste Summenformel überhaupt und war, wie auch die Summenformel für die ersten n Quadratzahlen, bereits in der vorgriechischen Mathematik bekannt.

Carl Friedrich Gauß hat diese Formel als 9-jähriger Schüler wiederentdeckt. Die Geschichte ist durch Wolfgang Sartorius von Waltershausen (1809–1876) überliefert: „Der junge Gauss war kaum in die Rechenclasse eingetreten, als Büttner die Summation der arithmetischen Reihe aufgab. Die Aufgabe war indes kaum ausgesprochen als Gauss die Tafel mit den im niedern Braunschweiger Dialekt gesprochenen Worten auf den Tisch wirft: »Dor ligget se.« (Da liegen sie.)“ Die genaue Aufgabenstellung ist nicht überliefert. Oft wird berichtet, dass Büttner die Schüler die Zahlen von 1 bis 100 (nach anderen Quellen von 1 bis 60) addieren ließ und Gauß feststellte, dass die erste und die letzte Zahl (1+100), die zweite und die vorletzte Zahl (2+99) usw. zusammen immer 101 ergeben. Der Wert der gesuchten Summe ergibt sich so zu 101 mal 50.

Entsprechend den damaligen Verhältnissen unterrichtete Büttner etwa 100 Schüler in einer Klasse. Damals waren auch Züchtigungen mit der sogenannten Karwatsche üblich. Sartorius berichtet: „Am Ende der Stunde wurden daraufhin die Rechentafeln umgekehrt; die von Gauss mit einer einzigen Zahl lag oben und als Büttner das Exempel prüfte, wurde das seinige zum Staunen aller Anwesenden als richtig befunden, während viele der übrigen falsch waren und alsbald mit der Karwatsche rectifizirt wurden.“ Büttner erkannte bald, dass Gauß in seiner Klasse nichts mehr lernen konnte.

Beweis

Für diese Summenformel gibt es zahlreiche Beweise. Neben dem oben vorgeführten Beweis der vorwärts- und rückwärts-Summation ist noch der folgende interessant: Man summiert die binomische Formel (1 + k)² = 1 + 2k + k² über k = 1 bis k = n:

$\begin{align} (1+1)^2 &= 1+2\cdot1+1^2\\ (1+2)^2 &= 1+2\cdot2+2^2\\ &\;\,\vdots\\ (1+n)^2 &= 1+2\cdot n+n^2 \end{align}$

und erhält:

$(1+n)^2 = n + 2(1+2+\dotsb+n) + 1^2$

also

$2(1+2+\dotsb+n) = (1+n)^2-n-1^2 = n^2+n = n(n+1)$.

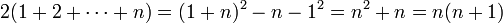Der Vorteil dieses Beweises liegt darin, dass er sich leicht auf Potenzsummen übertragen lässt. Ein Beweis der gaußschen Summenformel lässt sich auch mithilfe des Verfahrens der vollständigen Induktion führen.

Literatur

• Otto Neugebauer. Vorlesungen über Geschichte der antiken mathematischen Wissenschaften. Erster Band. Vorgriechische Mathematik. Springer, 1969. S.172-173
• Wolfgang Sartorius v. Waltershausen. Gauss zum Gedächtniss. Leipzig: Hirzel, 1856. S.12-13