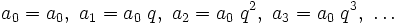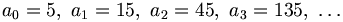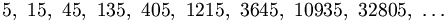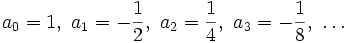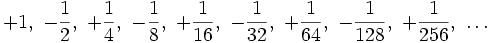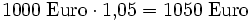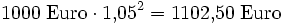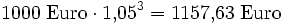Geometrische Progression

Eine geometrische Folge ist eine regelmäßige mathematische Zahlenfolge mit der Eigenschaft, dass das Verhältnis zweier benachbarter Folgenglieder konstant ist. Das $i$ -te Glied $a i$ einer geometrischen Folge mit dem Anfangsglied $a 0$ und dem Quotient $q$ berechnet sich aus

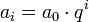$a_i = a_0 \cdot q^i$ (explizite Formel)

beziehungsweise aus

$a_0=a_0,\ a_1=a_0\;q,\ a_2=a_0\;q^2,\ a_3=a_0\;q^3,\ \dots$

Sind $a 0$ und $q$ positive reelle Zahlen, so ist jedes Glied $a i$ mit $i > 0$ das geometrische Mittel seiner Nachbarglieder $a i - 1$ und $a i + 1$ . Diese Tatsache ist der Grund für die Bezeichnung „geometrische Folge“. Die Summation der Folgenglieder ergibt die geometrische Reihe. Die Glieder einer Geometrischen Folge lassen sich auch aus dem jeweils vorhergehenden Glied berechnen, dazu dient die folgende Formel:

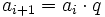$a_{i+1} =a_i \cdot q$ (rekursive Formel)

Neben der in diesem Artikel gewählten Darstellung ist es auch üblich, das erste Folgenglied mit $a 1$ zu bezeichnen.

Inhaltsverzeichnis

1 Zahlenbeispiele
- 1.1 Beispiel 1
- 1.2 Beispiel 2
2 Anwendungsbeispiele
- 2.1 Zinseszins
- 2.2 Gleichstufige Stimmung
3 Siehe auch
4 Weblinks

Zahlenbeispiele

Beispiel 1

Die Glieder der geometrischen Folge mit dem Anfangsglied $a 0 = 5$ und dem Quotienten $q = 3$ sind

$a_0=5,\ a_1=15,\ a_2=45,\ a_3=135,\ \dots$

wenn man die Glieder einfach hintereinander schreibt ergibt sich

$5,\ 15,\ 45,\ 135,\ 405,\ 1215,\ 3645,\ 10935,\ 32805,\ \dots$

Beispiel 2

Die Glieder der geometrischen Folge mit dem Anfangsglied $a 0 = 1$ und dem Quotienten 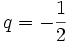$q=-\frac{1}{2}$ sind

$a_0=1,\ a_1=-\frac{1}{2},\ a_2=\frac{1}{4},\ a_3=-\frac{1}{8},\ \dots$

wenn man die Glieder einfach hintereinander schreibt ergibt sich

$+1,\ -\frac{1}{2},\ +\frac{1}{4},\ -\frac{1}{8},\ +\frac{1}{16} ,\ -\frac{1}{32},\ +\frac{1}{64},\ -\frac{1}{128},\ +\frac{1}{256},\ \dots$

Anwendungsbeispiele

Die geometrische Folge beschreibt Wachstumsprozesse, bei denen sich die Messgröße zum Zeitpunkt $n + 1$ aus der Messgröße zum Zeitpunkt $n$ durch Multiplikation mit einem konstanten Faktor $q$ ergibt. Zum Beispiel

Zinseszins

Bei einem Zinssatz von 5 Prozent vermehrt sich das Kapital jedes Jahr um den Faktor 1,05. Es handelt sich also um eine geometrische Folge mit dem Verhältnis $q = 1,05$ . Die Zahl $q$ heißt hier Zinsfaktor. Bei einem Startkapital von 1000 Euro ergibt sich

nach einem Jahr ein Kapital von

$1000\;\mathrm{Euro} \cdot 1{,}05 = 1050 \;\mathrm{Euro}$

nach zwei Jahren ein Kapital von

$1000\;\mathrm{Euro} \cdot 1{,}05^2= 1102{,}50 \;\mathrm{Euro}$

nach drei Jahren ein Kapital

$1000\;\mathrm{Euro} \cdot 1{,}05^3= 1157{,}63 \;\mathrm{Euro}$

und so weiter.

Gleichstufige Stimmung

Es gibt mehrere Arten, wie ein Musikinstrument gestimmt werden kann. Eine davon ist die gleichstufige Stimmung. Bei ihr ist das Frequenzverhältnis zwischen zwei benachbarten Tönen immer konstant. Bei zwölf Tönen in der Oktave lautet die Folge hier:

$f(i) = a_0 \cdot \left(\sqrt[12]{2}\,\right) ^i$ ,

wobei $a 0$ beispielsweise die Frequenz des Kammertons, und $i$ die Halbtonschrittentfernung zum Kammerton ist. $f (i)$ ist dann die Frequenz des gesuchten Tones mit Halbtonabstand $i$ zum "Ursprungston" $a 0$ .

Der Wachstumsfaktor ist also $q = \sqrt[12]{2}$ .

Siehe auch

Weblinks

Schülergerechte Erklärungen

Wikimedia Foundation.

Игры ⚽ Нужно сделать НИР?

Schlagen Sie auch in anderen Wörterbüchern nach:

Geometrische Progression — Geometrische Progression, s. Progression … Kleines Konversations-Lexikon
Geometrische Progression — Geometrische Progression, s. Reihe … Meyers Großes Konversations-Lexikon
Progression — Pro|gres|si|on, die; , en (das Fortschreiten; [Stufen]folge, Steigerung; Steuerwesen unverhältnismäßige Zunahme des Steuersatzes bei geringfügig steigendem Einkommen; Mathematik veraltet Aufeinanderfolge von Zahlen usw.); kalte Progression;… … Die deutsche Rechtschreibung
Progression — (v. lat.), 1) Fortschreiten, Stufenfolge, Stufengang; 2) (Math.), die Aufeinanderfolge von Größen od. Zahlen (Glieder), welche nach einem gewissen Gesetze wachsen od. abnehmen. Ist die Differenz zwei auf einander folgender Glieder stets dieselbe … Pierer's Universal-Lexikon
Arithmetische Progression — Eine arithmetische Folge oder arithmetische Progression ist eine regelmäßige mathematische Zahlenfolge mit der Eigenschaft, dass die Differenz zweier benachbarter Folgenglieder konstant ist. Also ai + 1 = ai + d (rekursive Formel) Das i te Glied… … Deutsch Wikipedia
Reihe — Reihe, 1) mehre in einer Linie neben einander befindliche Dinge; 2) das Aufeinanderfolgen nach festgesetzter Ordnung; 3) jede Folge von Größen (die Glieder [Termini] derselben genannt), welche nach einem bestimmten Gesetz gebildet sind. Die R n… … Pierer's Universal-Lexikon
Reihe [1] — Reihe, in der Mathematik jede nach einem bestimmten Gesetze gebildete Folge von Größen; diese Größen nennt man die Glieder der R. und bezeichnet sie, mit dem Anfangsglied beginnend, als erstes, zweites etc. Glied der R. Versteht man unter n eine… … Meyers Großes Konversations-Lexikon
Magisches Quadrat — Magisches Quadrat, 1) ein in gleiche Fächer eingetheiltes Quadrat, worin Zahlen einer Folgereihe so eingetragen sind, daß ihre Summen in jedem horizontalen u. jedem perpendiculären Streifen, eben so aber auch längs jeder Diagonale, gleich groß… … Pierer's Universal-Lexikon
Geometrisch — Geometrisch, was zur Geometrie gehört; so: Geometrische Linie, zieht man aus der natürlichen Zahlenreihe die zweiten Wurzeln u. trägt diese in einem beliebigen Maßstabe auf einer Linie von einem u. demselben Punkte aus auf, so ist die so… … Pierer's Universal-Lexikon
Zinsrechnung — (Interessenrechnung; hierzu Textbeilage »Zinsberechnungstabellen«) und Rentenrechnung, die verschiedenen Rechnungsarten, die zur Auflösung aller der Aufgaben dienen, die bei der Anlegung zinstragender Kapitalien vorkommen. Bei der Z. kommen in… … Meyers Großes Konversations-Lexikon

Academic dictionaries and encyclopedias

Geometrische Progression

Inhaltsverzeichnis