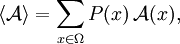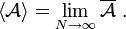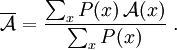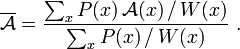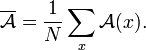Gewichtabtastung

Importance Sampling ist ein Begriff aus dem Bereich der stochastischen Prozesse, der die Technik zur Erzeugung von Stichproben anhand einer Wahrscheinlichkeitsverteilung beschreibt. Importance Sampling wird benutzt, um die Effektivität von Monte-Carlo-Simulationen zu steigern.

Beispiel

Monte-Carlo-Simulationen werden oft benutzt, um Erwartungswerte einer Größe $\mathcal{A}$,

$\left\langle \mathcal{A} \right\rangle = \sum_{x \in \Omega} P(x) \, \mathcal{A}(x),$

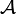zu berechnen, wobei P(x) ein normiertes statistisches Gewicht wie beispielsweise ein Boltzmanngewicht ist. 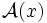$\mathcal{A}(x)$ ist der Wert der Größe 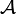$\mathcal{A}$ im Zustand x. Die Summation (Integration) verläuft dabei über einen Raum Ω, z. B. dem Phasenraum der Teilchen im System.

Der Erwartungswert kann durch Mittelwertbildung berechnet werden, da für den Limes des Mittelwertes gilt:

$\left\langle \mathcal{A} \right\rangle = \lim_{N \to \infty} \overline \mathcal{A} \ .$

Für den einfachsten Fall (Simple Sampling) zufällig ausgewählter Zustände ergibt der Mittelwert

$\overline \mathcal{A} = \frac{\sum_x P(x) \, \mathcal{A}(x)}{\sum_x P(x)} \ .$

Diese Methode ist meistens nicht sehr effektiv, da häufig nur wenige relevante Zustände in die Mittelwertbildung eingehen. Um dieses Problem zu umgehen und so die Standardabweichung des gemessenen Mittelwertes bei gleicher Anzahl von Stichproben zu reduzieren, versucht man Zustände mit einem größeren Gewicht häufiger in die Mittelwertbildung eingehen zu lassen als Zustände mit einem geringerem Gewicht.

Werden Zustände mit einer Wahrscheinlichkeit W(x) erzeugt (Importance Sampling), so berechnet sich der Mittelwert zu

$\overline \mathcal{A} = \frac{\sum_x P(x) \, \mathcal{A}(x) \,/\, W(x)}{\sum_x P(x) \,/\, W(x)} \ .$

Werden die Systemzustände mit der Wahrscheinlichkeit P(x) erzeugt, so ergibt sich

$\overline \mathcal{A} = \frac{1}{N}\sum_x \mathcal{A}(x).$

Um dies in der Praxis zu erreichen, geht man von einer Startkonfiguration aus und erzeugt eine Markov-Kette aus Systemzuständen.

Siehe auch

• Metropolisalgorithmus

Literatur

• W.K. Hastings: Monte Carlo Sampling Methods Using Markov Chains and Their Applications. In: Biometrika. 57, 1970, S. 97-109. 
• R. Srinivasan: Importance sampling - Applications in communications and detection. Springer-Verlag, Berlin 2002, ISBN 978-3-540-43420-7.