- Gewichteter Automat
-
Der gewichtete Automat ist ein mathematisches Konzept aus der theoretischen Informatik, speziell aus der Automatentheorie. Es ist eine Verallgemeinerung des Automaten. Während die Transitionen eines (deterministischen oder nichtdeterministischen) Automaten mit Buchstaben des zugrundeliegenden Alphabets beschriftet sind, wird den Transitionen eines gewichteten Automaten zusätzlich ein bestimmtes Gewicht zugeordnet. Es kann zum Beispiel als Aufwand interpretiert werden der betrieben werden muss, um vom einen Zustand zum anderen zu gelangen, während eine bestimmte Aktion durchgeführt wird.
Mathematische Definition
Sei
 ein Halbring, Q eine nichtleere Menge und Σ ein Alphabet. Ein Fünftupel
ein Halbring, Q eine nichtleere Menge und Σ ein Alphabet. Ein Fünftupel  heißt gewichteter Automat mit Kosten (Gewichten) in
heißt gewichteter Automat mit Kosten (Gewichten) in  , falls:
, falls:  ,
,  und
und  . δ ist dann die Transitionsfunktion, λ sind die Einstiegsgewichte und θ die Ausstiegsgewichte.
. δ ist dann die Transitionsfunktion, λ sind die Einstiegsgewichte und θ die Ausstiegsgewichte.Ein Pfad in einem gewichteten Automaten ist eine Folge
 , wobei
, wobei  Zustände und
Zustände und  Buchstaben sind. Die Beschriftung dieses Pfades lautet
Buchstaben sind. Die Beschriftung dieses Pfades lautet  . Das Gewicht eines solchen Pfades beträgt
. Das Gewicht eines solchen Pfades beträgt  . Also wird das Einstiegsgewicht mit den Gewichten der Transitionen und dem Ausstiegsgewicht multipliziert. Um für ein Wort
. Also wird das Einstiegsgewicht mit den Gewichten der Transitionen und dem Ausstiegsgewicht multipliziert. Um für ein Wort  das Gewicht zu berechnen, addiert der Automat die Gewichte aller Pfade mit der Beschriftung w zusammen. Die von einem Automaten berechnete Funktion
das Gewicht zu berechnen, addiert der Automat die Gewichte aller Pfade mit der Beschriftung w zusammen. Die von einem Automaten berechnete Funktion  heißt auch formale Potenzreihe.
heißt auch formale Potenzreihe.Beispiele
Ein Halbring, der bei gewichteten Automaten oft betrachtet wird ist der tropische Halbring,
 wobei
wobei  das neutrale Element bezüglich der Minimumsbildung und 0 das neutrale Element bezüglich der Addition ist. Bei Automaten über diesem Halbring ist Gewicht eines Wortes w das Minimum der Gewichte aller Pfade mit der Beschriftung w. Ein sehr konkretes Beispiel für einen gewichteten Automaten über
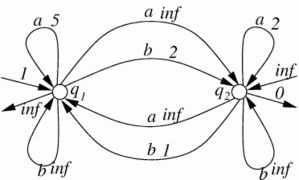
das neutrale Element bezüglich der Minimumsbildung und 0 das neutrale Element bezüglich der Addition ist. Bei Automaten über diesem Halbring ist Gewicht eines Wortes w das Minimum der Gewichte aller Pfade mit der Beschriftung w. Ein sehr konkretes Beispiel für einen gewichteten Automaten über  ist
istzum Beispiel betragen hier die Einstiegskosten für q1 1. Die Transitionskosten von q1 nach q2 betragen für a
 und für b 2. Da im tropischen Halbring die erste Operation ("Addition") die Minimumbildung ist und die zweite Operation die Addition, ist für ein gegebenes Wort das Gewicht gerade das Minimum aller Summen entlang von Pfaden die mit diesem Wort beschriftet sind. Für das Wort aba ist zum Beispiel der Pfad
und für b 2. Da im tropischen Halbring die erste Operation ("Addition") die Minimumbildung ist und die zweite Operation die Addition, ist für ein gegebenes Wort das Gewicht gerade das Minimum aller Summen entlang von Pfaden die mit diesem Wort beschriftet sind. Für das Wort aba ist zum Beispiel der Pfad  der einzige Pfad mit endlichem Gewicht und damit der minimale Pfad. Also sind die Kosten von aba genau 5.
der einzige Pfad mit endlichem Gewicht und damit der minimale Pfad. Also sind die Kosten von aba genau 5.Ein weiterer Halbring ist der Boolesche Halbring,
 mit den beiden logischen Operationen "und" und "oder" und den neutralen Elementen "0"(=falsch) bezüglich "oder" und "1"(=wahr) bezüglich "und". Jeder endliche Automat
mit den beiden logischen Operationen "und" und "oder" und den neutralen Elementen "0"(=falsch) bezüglich "oder" und "1"(=wahr) bezüglich "und". Jeder endliche Automat  (nicht gewichtet) hat genau einen korrespondierenden Booleschen Automat
(nicht gewichtet) hat genau einen korrespondierenden Booleschen Automat  . Die Transitionen von
. Die Transitionen von  koennen dabei in Transitionen in
koennen dabei in Transitionen in  übersetzt werden die das Gewicht "1" haben. Alle anderen Transitionen in
übersetzt werden die das Gewicht "1" haben. Alle anderen Transitionen in  haben dann das Gewicht "0". In
haben dann das Gewicht "0". In  haben dann genau die Pfade das Gewicht "1", die in
haben dann genau die Pfade das Gewicht "1", die in  existieren. Daher sind gewichtete Automaten ein allgemeineres Konzept als endliche Automaten.
existieren. Daher sind gewichtete Automaten ein allgemeineres Konzept als endliche Automaten.
Wikimedia Foundation.