Gitterkusszahl

In der Geometrie ist die Kusszahl (auch Kontaktzahl) die maximale Anzahl von Kugeln mit Radius 1, die gleichzeitig die Einheitskugel im n-dimensionalen euklidischen Raum berühren können, ohne dass Überschneidungen auftreten. Zusätzlich kann die Bedingung aufgestellt werden, dass die Mittelpunkte der Kugeln in einem Gitter liegen (Gitterkusszahl).

Kusszahlen in verschiedenen Dimensionen

In einer Dimension ist die Einheitskugel eine Strecke, deren Endpunkte den Abstand 1 vom Ursprung haben. Hier kann an beide Endpunkte jeweils eine weitere Strecke angefügt werden, sodass die die Kusszahl für eine Dimension offensichtlich 2 ist:

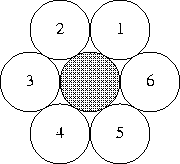
In der zweiten Dimension ist die Einheitskugel ein Kreis mit Radius 1. Anschaulich entspricht damit das Problem der Ermittlung der Kusszahl in dieser Dimension der Aufgabe, möglichst viele Münzen so anzuordnen, dass sie alle eine gleich große zentrale Münze berühren. Es ist leicht zu sehen (und zu beweisen), dass die Kusszahl für die zweite Dimension 6 ist:

In der dritten Dimension ist die Berechnung nicht so einfach. Es ist leicht, zwölf Kugeln so anzuordnen, dass sie die zentrale Kugel berühren, aber dabei bleibt eine Menge Platz übrig, und es ist nicht offensichtlich, dass dieser Platz nicht ausreicht, um eine dreizehnte Kugel hinzuzufügen. Tatsächlich ist so viel Platz vorhanden, dass zwei beliebige Kugeln aus den zwölf äußeren ihre Plätze tauschen können, ohne den Kontakt zur zentralen Kugel zu verlieren. Dieses Problem war Thema einer berühmten Streitigkeit zwischen den Mathematikern Isaac Newton und David Gregory, die beide 1692 anlässlich einer Diskussion zur Keplerschen Vermutung führten. Newton behauptete, das Maximum wäre zwölf, Gregory meinte, es wäre dreizehn. Im 19. Jahrhundert erschienen mit (Lit.: Bender 1874), (Lit.: Günther 1875) und (Lit.: Hoppe 1874) die ersten Veröffentlichungen, die behaupteten, den Beweis für Newtons Behauptung zu enthalten. Nach heutigen Standards wurden formelle Beweise jedoch erst 1953 von (Lit.: Schütte, van der Waerden) und 1956 von (Lit.: Leech 1965) erbracht.

Die Kusszahlen für den n-dimensionalen Raum sind für n>3 unbekannt, mit Ausnahme von n=8 (240) und n=24 (196.560). Für n=4 ist seit einiger Zeit bekannt, dass die Kusszahl entweder 24 oder 25 ist. Die Anordnung von 24 Kugeln um eine zentrale Kugel ist relativ einfach, aber, vergleichbar mit dem dreidimensionalen Fall, ist eine Menge Platz übrig, sogar mehr als im dreidimensionalen Fall. Die Situation ist hier also noch unklarer. Im 24-dimensionalen Raum werden die Kugeln auf den Punkten des Leech-Gitters platziert, sodass kein Platz übrig ist. Die folgende Tabelle gibt die Kusszahl bis zur Dimension 24 wieder:

Dimension Kusszahl untere Grenze obere Grenze 1 2 2 6 3 12 4 24 25 5 40 46 6 72 82 7 126 140 8 240 9 306 380 10 500 595 11 582 915 12 840 1.416

Dimension Kusszahl untere Grenze obere Grenze 13 1.130 2.233 14 1.582 3.492 15 2.564 5.431 16 4.320 8.313 17 5.346 12.215 18 7.398 17.877 19 10.688 25.901 20 17.400 37.974 21 27.720 56.852 22 49.896 86.537 23 93.150 128.096 24 196.560

Die exakten Kusszahlen für die Dimensionen 8 und 24 wurden 1979 von (Lit.: Levenshtein 1979) und (Lit.: Odlyzko, Sloane 1979) unabhängig voneinander ermittelt. Schätzungen zeigen, dass das Wachstum der Kusszahlen exponentiell ist. Die Basis des exponentiellen Wachstums ist unbekannt.

Gitterkusszahlen in verschiedenen Dimensionen

Die exakten Gitterkusszahlen sind für die Dimensionen 1 bis 9 und für die Dimension 24 bekannt (Lit.: Conway, Sloane 1992), (Lit.: Sloane, Nebe). Die folgende Tabelle gibt die Gitterkusszahl bis zur Dimension 24 wieder:

Dimension Gitterkusszahl 1 2 2 6 3 12 4 24 5 40 6 72 7 126 8 240 9 272 10 ≥ 336 11 ≥ 438 12 ≥ 756

Dimension Gitterkusszahl 13 ≥ 918 14 ≥ 1.422 15 ≥ 2.340 16 ≥ 4.320 17 ≥ 5.346 18 ≥ 7.398 19 ≥ 10.668 20 ≥ 17.400 21 ≥ 27.720 22 ≥ 49.896 23 ≥ 93.150 24 196.560

Die Gitterpackungen für die Dimensionen 12 und 24 haben eigene Namen: Das Coxeter-Todd Gitter (nach Harold Scott MacDonald Coxeter und John Arthur Todd) für die Dimension 12 und das Leech Gitter (nach John Leech) für die Dimension 24.

Die allgemeine Form der unteren Grenze für n-dimensionale Gitterkennzahlen definiert durch

$\eta \geq \frac{\zeta(n)}{2^{n-1}}$,

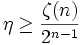wobei ζ(n) die Riemannsche Zeta-Funktion ist, ist als Satz von Minkowski-Hlawka (nach Hermann Minkowski und Edmund Hlawka) bekannt.

Siehe auch

• dichteste Kugelpackung

Literatur

• C. Bender: Bestimmung der größten Anzahl gleich Kugeln, welche sich auf eine Kugel von demselben Radius, wie die Übrigen, auflegen lassen. Archiv Math. Physik (Grunert) 56, 1874. S. 302—306.
• John Horton Conway, Neil J. A. Sloane: The Kissing Number Problem. und Bounds on Kissing Numbers. In: John Horton Conway, Neil J. A. Sloane: Sphere Packings, Lattices, and Groups. 2. Auflage. Springer-Verlag, New York 1993. S. 21-24 und 337—339, ISBN 0387985859.
• S. Günther: Ein stereometrisches Problem. Archiv Math. Physik 57, 1875. S.209—215.
• R. Hoppe: Bemerkung der Redaction. Archiv Math. Physik. (Grunert) 56, 1874. S. 307—312.
• John Leech: The Problem of Thirteen Spheres. In: The Mathematical Gazette 40, 1956. S. 22-23.
• Vladimir I. Levenshtein: О границах для упаковок в n-мерном евклидовом пространстве. Nr. 6, Dokl. Akad. Nauk SSSR 245 1979. S. 1299—1303.
• Andrew M. Odlyzko, Neil J. A. Sloane: New bounds on the number of unit spheres that can touch a unit sphere in n dimensions. J. Combin. Theory Ser. A 26, 1979, Nr. 2, S. 210—214.
• Neil J. A. Sloane, Gabriele Nebe. Table of Highest Kissing Numbers Presently Known. http://www.research.att.com/~njas/lattices/kiss.html.
• Karl Schütte, Bartel Leendert van der Waerden: Das Problem der dreizehn Kugeln. Math. Annalen 125, 1953. S. 325-334.

Weblinks

• Robert Calderbank: Interview with Neil Sloane (englisch)