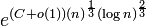Gittersieb

Das Zahlkörpersieb (Number Field Sieve) ist ein Begriff aus dem mathematischen Teilgebiet der Zahlentheorie. Es ist einer der schnellsten bekannten Algorithmen zur Faktorisierung großer Zahlen.

Das Zahlkörpersieb wird vor allem für Zahlen mit über 100 Stellen benutzt, die durch andere Verfahren nicht zerlegt werden konnten. Typischerweise werden dabei mehrere 100 Rechner parallel betrieben.

Entstehungsgeschichte

1988 schrieb John M. Pollard einen Brief an A. M. Odlyzko mit Kopien an R. P. Brent, J. Brillhart, H. W. Lenstra, C. P. Schnorr und H. Suyama, worin er ein neues Faktorisierungsverfahren für ganz spezielle Zahlen beschrieb. In diesem Brief illustrierte er dieses Verfahren an der Fermat-Zahl F₇ und vermutete, dass damit die bis dato noch nicht faktorisierte Zahl F₉ möglicherweise ein Kandidat für dieses Verfahren ist. Pollard benutzte aber noch kein Siebverfahren im algebraischen Zahlkörper.

In den Folgejahren wurde diese Idee unter anderem von A. K. Lenstra, H. W. Lenstra, M. S. Manasse und J. M. Pollard ausgebaut. Daraus entstand das spezielle Zahlkörpersieb (wie das Verfahren heutzutage bezeichnet wird, um es vom allgemeinen Zahlkörpersieb unterscheiden zu können). Das spezielle Zahlkörpersieb lässt sich nur für Zahlen der Form b^m − r mit b, r klein und m groß anwenden.

Das allgemeine Zahlkörpersieb wurde annähernd zeitgleich zum speziellen Zahlkörpersieb von J. P. Buhler, H. W. Lenstra und Carl Pomerance gefunden. Dieses ist für beliebige Zahlen anwendbar, dafür muss man aber Einbußen bei der Geschwindigkeit hinnehmen.

1992 gelang mit Hilfe des speziellen Zahlkörpersiebs die Faktorisierung von F₉.

Bereits 1991 publizierte Pollard eine Variante des Zahlkörpersiebs, bei der ein zweidimensionales Sieb benutzt wird, welches er als Gittersieb bezeichnet. Mit dieser Gittersiebvariante, kombiniert mit anderen Methoden, wurde von 2003 bis 2005 eine 200-stellige Dezimalzahl (genannt RSA-200) faktorisiert^[1].

Asymptotische Laufzeit

Die asymptotische Laufzeit des Zahlkörpersiebs konnte bislang nicht exakt bewiesen werden. Unter einigen, als wahrscheinlich geltenden Annahmen, kann man diese jedoch zu

$e^{(C+o(1))(n)^\frac13(\log n)^\frac23}$

berechnen. n bezeichnet hierbei die Bitlänge der Zahl. Dabei ist die Konstante C davon abhängig, ob das spezielle oder das allgemeine Zahlkörpersieb benutzt wird:

• Spezielles Zahlkörpersieb: C=(32/9)^1/3
• Allgemeines Zahlkörpersieb: C=(64/9)^1/3

Literatur

• Carl Pomerance: A Tale of Two Sieves, Notices of the AMS, 43 (1996) 1473-1485 (Webversion: http://www.ams.org/notices/199612/pomerance.pdf )
• A. K. Lenstra & H. W. Lenstra, Jr.: The development of the number field sieve, Lecture Notes in Mathematics, V. 1554, 1993

Weblinks

• http://www.informatik.tu-darmstadt.de/KP/theses/Katja_Schmidt-Samoa.diplom.pdf - Das Number Field Sieve: Entwicklung, Varianten und Erfolge von Katja Schmidt-Samoa.

Einzelnachweise

1. ↑ Meldung der Faktorisierung von RSA-200