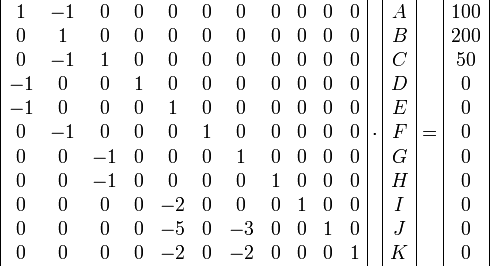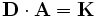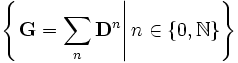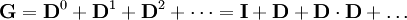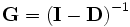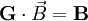Gozinto-Matrix

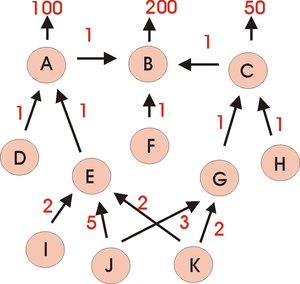
Der Gozintograph ist ein gerichteter Graph, der beschreibt, aus welchen Teilen sich ein oder mehrere Produkte zusammensetzen. Der Produktionsprozess kann dabei mehrstufig sein, wobei der Input aus Rohstoffen, Halb- und Fertigteilen besteht. Im Gozintographen ist aufgeführt, wie diese Teile gegebenenfalls mengenmäßig verflochten sind. Dabei bezeichnen die Knoten die Teile und die gerichteten Kanten geben an, wie viele Einheiten eines Teiles in eine Einheit eines nachgelagerten Teiles einfließen.

Der Name dieses Graphen ist eine scherzhafte Verballhornung: Der Mathematiker Andrew Vazsonyi gab als Urheber den (fiktiven) italienischen Mathematiker Zepartzat Gozinto an, was nichts anderes bedeutet als „the part that goes into“. Diese Bezeichnung ist mittlerweile allgemein akzeptiert.

Der Gozintograph wird vor allem im Bereich der Produktionsplanung und -steuerung für die Auflösung von Stücklisten angewendet. Die Inhalte des Graphen können in ein lineares Gleichungssystem eingebracht werden. Es ergeben sich dann meistens sehr große, dünnbesetzte Koeffizientenmatrizen, die je nach Struktur unterschiedliche Lösungsverfahren ermöglichen.

Beispiel

Im folgenden stark vereinfachten Beispiel sollen für einen Heimwerkermarkt 200 Verlängerungskabel, 100 Stecker und 50 Dosen produziert werden. Die Endprodukte setzen sich aus verschiedenen Teilen zusammen, Stiften, Schrauben, Schellen, Innenteile, Deckel usw. In der folgenden Tabelle sind die einzelnen Teile aufgelistet.

Gozintograph für die Erstellung der Elektroartikel

Symbol	Teil
A	Stecker
B	Verlängerungskabel
C	Steckdose
D	Deckelsatz Stecker
E	Korpus Stecker
F	Kabel
G	Korpus Dose
H	Deckelsatz Dose
I	Stift
J	Schraube
K	Schelle

Die Verflechtungen können in ein Gleichungssystem überführt werden. Es wird zunächst aufgeführt, wie viele Einheiten von einem Teil gebraucht werden.

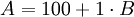
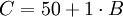
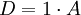
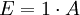
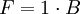
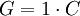
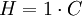
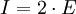
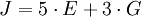
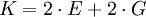
$A=100+1\cdot{B}$	B = 200	$C=50+1\cdot{B}$	$D=1\cdot{A}$	$E=1\cdot{A}$	$F=1\cdot{B}$
$G=1\cdot{C}$	$H=1\cdot{C}$	$I=2\cdot{E}$	$J=5\cdot{E}+3\cdot{G}$	$K=2\cdot{E}+2\cdot{G}$

Variante 1

Aufgrund der einfachen Struktur dieses Beispiels können die einzelnen Gleichungen sukzessive gelöst werden. Es wird benötigt:

A = 300	B = 200	C = 250	D = 300	E = 300	F = 200
G = 250	H = 250	I = 600	J = 2.250	K = 1.100

Wenn eine Koeffizientenmatrix erstellt werden soll, wandelt man die Gleichungen entsprechend um, z. B.:

$1\,A=100+1\,B\Leftrightarrow{1\,A-1\,B=100}$

Die Konstanten dieser Gleichungen fasst man dann in der erweiterten Koeffizientenmatrix zusammen, die in den Zellen der folgenden Tabelle enthalten ist:

$\begin{array}{|ccccccccccc|} 1&-1&0&0&0&0&0&0&0&0&0\\ 0&1&0&0&0&0&0&0&0&0&0\\ 0&-1&1&0&0&0&0&0&0&0&0\\ -1&0&0&1&0&0&0&0&0&0&0\\ -1&0&0&0&1&0&0&0&0&0&0\\ 0&-1&0&0&0&1&0&0&0&0&0\\ 0&0&-1&0&0&0&1&0&0&0&0\\ 0&0&-1&0&0&0&0&1&0&0&0\\ 0&0&0&0&-2&0&0&0&1&0&0\\ 0&0&0&0&-5&0&-3&0&0&1&0\\ 0&0&0&0&-2&0&-2&0&0&0&1 \end{array} \cdot\begin{array}{|c|}A\\B\\C\\D\\E\\F\\G\\H\\I\\J\\K\end{array} =\begin{array}{|c|}100\\200\\50\\0\\0\\0\\0\\0\\0\\0\\0\end{array}$

Variante 2

Alternativ bildet man aus den obenstehenden Gleichungssystem direkt die Direktbedarfsmatrix D (dh. ohne Umformung des Gleichungssystems):

$\mathbf{D}\cdot\mathbf{A}=\mathbf{K}$

$\begin{array}{|ccccccccccc|} 0&1&0&0&0&0&0&0&0&0&0\\ 0&0&0&0&0&0&0&0&0&0&0\\ 0&1&0&0&0&0&0&0&0&0&0\\ 1&0&0&0&0&0&0&0&0&0&0\\ 1&0&0&0&0&0&0&0&0&0&0\\ 0&1&0&0&0&0&0&0&0&0&0\\ 0&0&1&0&0&0&0&0&0&0&0\\ 0&0&1&0&0&0&0&0&0&0&0\\ 0&0&0&0&2&0&0&0&0&0&0\\ 0&0&0&0&5&0&3&0&0&0&0\\ 0&0&0&0&2&0&2&0&0&0&0 \end{array} \cdot\begin{array}{|c|}A\\B\\C\\D\\E\\F\\G\\H\\I\\J\\K\end{array} =\begin{array}{|c|}100\\200\\50\\0\\0\\0\\0\\0\\0\\0\\0\end{array}$

Anschließend berechnet man die Gesamtbedarfsmatrix G:

$\left\{ \left. \mathbf{G} = \sum_n{\mathbf{D}^n} \right| n\in\left\{ 0,\mathbb{N}\right\} \right\}$

Das bedeutet man berechnet

$\mathbf{G}=\mathbf{D}^0+\mathbf{D}^1+\mathbf{D}^2+\dots =\mathbf{I}+\mathbf{D}+\mathbf{D}\cdot\mathbf{D}+\dots$

Dies macht man so lange, bis man ein 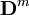$\mathbf{D}^m$ findet das gleich Null ist, da in diesem Fall 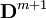$\mathbf{D}^{m+1}$ ebenfalls Null ist und sich daher das Ergebnis nicht mehr ändert. Dies ist der Fall, wenn n größer ist als die maximale Anzahl der Schritte die zur Erstellung des Endproduktes aus den Anfangsprodukten benötigt werden. Allgemein ist 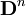$\mathbf{D}^n$ die Matrix welche angibt, wie viele Einheiten des Produkts aus Zwischenprodukten bzw. Rohstoffen über n-1 Zwischenschritte hergestellt werden. 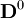$\mathbf{D}^0$ ist hierbei die Einheitsmatrix $\mathbf{I}$.

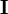Alternativ kann man auch die Gleichung

$\mathbf{G}=\left( \mathbf{I}-\mathbf{D}\right)^{-1}$

lösen.

Man erhält somit:

$\mathbf{G}=\begin{array}{|ccccccccccc|} 1&-1&0&0&0&0&0&0&0&0&0\\ 0&1&0&0&0&0&0&0&0&0&0\\ 0&-1&1&0&0&0&0&0&0&0&0\\ -1&0&0&1&0&0&0&0&0&0&0\\ -1&0&0&0&1&0&0&0&0&0&0\\ 0&-1&0&0&0&1&0&0&0&0&0\\ 0&0&-1&0&0&0&1&0&0&0&0\\ 0&0&-1&0&0&0&0&1&0&0&0\\ 0&0&0&0&-2&0&0&0&1&0&0\\ 0&0&0&0&-5&0&-3&0&0&1&0\\ 0&0&0&0&-2&0&-2&0&0&0&1 \end{array}$

Diese Lösung ist äquivalent zur Lösung der ersten Variante.

Anwendung

Will man nun nach Ermittlung der Bedarfsmatrix wissen wie viele Teile benötigt, wenn ein bestimmter Bedarf an den Endprodukten A, B und C besteht, sowie ein bestimmter Lagervorrat an den Zwischenprodukten E und G sowie den Teilen D, F, H, I, J und K angelegt werden soll, wird aus dem Bedarf ein Bedarfsvektor 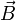$\vec{B}$ erstellt, welcher die entsprechende Anzahl beinhaltet. Der Bedarf B wird ermittelt, indem man das Produkt der Gesamtbedarfsmatrix mit dem Bedarfsvektor bildet:

$\mathbf{G}\cdot\vec{B}=\mathbf{B}$

Siehe auch

• Gozinto-Verfahren