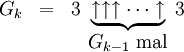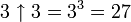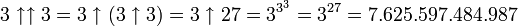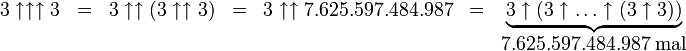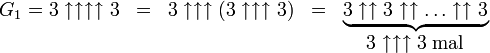Graham-Zahl

Grahams Zahl (nach Ronald L. Graham) ist eine spezielle, unvorstellbar große natürliche Zahl. Sie ist eine obere Grenze für ein Problem der Ramsey-Theorie und gilt als „die größte Zahl, die je in einem mathematischen Beweis verwendet wurde“.

Grahams Problemstellung

In einem n-dimensionalen Hyperwürfel (Einheitswürfel im n-dimensionalen Euklidischen Raum) seien alle 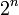$2^n\!\,$ Ecken (Knoten) je paarweise durch eine Linie (Kante) verbunden, so dass ein vollständiger Graph auf 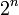$2^n\!\,$ Knoten entsteht, der somit 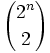${2^n\choose 2}$ Kanten besitzt.

Diese Kanten werden nun mit jeweils einer von zwei Farben eingefärbt. Die Frage ist dann, ob es einen vollständigen Teilgraphen aus vier in einer Ebene des Euklidischen Raums liegenden Knoten gibt, dessen sechs Kanten alle die gleiche Farbe haben.

In niedrigen Dimensionen gibt es Kantenfärbungen, wo dies nicht gilt. Bei 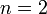$n=2\!\,$ besteht der Gesamtgraph nur aus einer Ebene mit vier Knoten. Färbt man diesen mit unterschiedlichen Farben, so besteht der einzige Teilgraph, nämlich der Gesamtgraph selbst, nicht aus sechs Kanten gleicher Farbe. 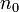Existiert andererseits eine Dimension $n_0\!\,$, in der für jede mögliche Kantenfärbung des Hyperwürfels ein Teilgraph mit diesen Eigenschaften existiert, so gilt dies auch für jede höhere Dimension $n \ge n_0$, da der Hyperwürfel einer höheren Dimension einen Hyperwürfel der Dimension $n_0\!\,$ als Teilgraph enthält, in dem der Teilgraph aus vier Knoten zu finden ist.

Daraus ergibt sich die eigentliche Problemstellung: wie groß ist das 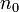$n_0\!\,$, mit dem für alle 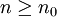$n \ge n_0$ für jede mögliche Kantenfärbung ein Teilgraph mit diesen Eigenschaften existiert, während es für alle 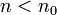$n < n_0\!\,$ eine Kantenfärbung gibt, die dies verhindert?

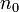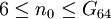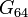Das Problem wurde noch nicht gelöst. Graham und Rothschild haben 1971 gezeigt, dass es einen solchen Wert $n_0\!\,$ gibt, und dass $6 \le n_0 \le G_{64}$ ist. $G_{64}\!\,$ wird Grahams Zahl genannt, und ist nachfolgend definiert.

Der Mathematiker Geoffrey Exoo von der Indiana State University verbesserte 2003 die untere Schranke auf $n_0 \ge 11$.

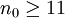Definition

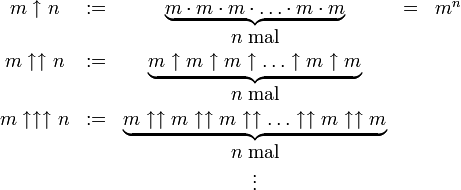
Grahams Zahl ist so extrem groß, dass nicht einmal Hilfsmittel wie der Hyperpotenz-Operator ausreichen, um die Definition dieser Zahl sinnvoll niederzuschreiben. Dieser Operator kann z. B. mit Knuths Pfeil-Schreibweise dargestellt werden. Für natürliche Zahlen 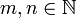$m,n\in\Bbb N$ definiert man:

$\begin{matrix} m\uparrow n & := & \underbrace{m\cdot m\cdot m\cdot \ldots \cdot m\cdot m} & = & m^n \\ & & {n\;\mathrm{mal}} \\ m\uparrow \uparrow n & := & \underbrace{m\uparrow m\uparrow m\uparrow \ldots\uparrow m\uparrow m} \\ & & {n\;\mathrm{mal}} \\ m\uparrow \uparrow \uparrow n & := & \underbrace{m\uparrow \uparrow m\uparrow \uparrow m\uparrow \uparrow \ldots\uparrow \uparrow m\uparrow \uparrow m} \\ & & {n\;\mathrm{mal}} \\ & & \vdots \end{matrix}$

Außerdem definiert man 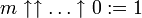$m \uparrow \uparrow \ldots \uparrow 0 := 1$. Statt 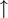$\uparrow$ wird oft auch das Symbol ^ verwendet.

In der ersten Zeile wird hierbei die übliche Potenz erklärt; ab der zweiten Zeile ist für das Verständnis zu beachten, dass der Potenzoperator 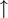$\uparrow$ nicht assoziativ ist. Der klammerfrei notierte Ausdruck $m\uparrow m\uparrow \ldots m\uparrow m$ ist deshalb mehrdeutig; in diesem Fall ist er - wie unter Mathematikern als Konvention üblich - von rechts nach links abzuarbeiten. Beispielsweise ist $m\uparrow m\uparrow m = m\uparrow (m\uparrow m)$. 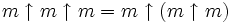Diese Reihenfolge ist auch gerade diejenige, bei der die größten Endergebnisse hervorgebracht werden.

Mit dieser Notation kann man die Folge (G_k) durch folgende Regeln rekursiv definieren:

G₀ = 4

$\begin{matrix} G_k & = & 3 \ \underbrace{\uparrow \uparrow \uparrow \cdots\uparrow } \ 3\\ & & {G_{k-1} \; \mathrm{mal}} \end{matrix}$

Grahams Zahl ist definiert als G₆₄.

Zur besseren Veranschaulichung, wie extrem groß Grahams Zahl ist, werden die ersten Schritte zur Berechnung von G₁ gezeigt:

$3\uparrow 3 = 3^3 = 27$

$3\uparrow \uparrow 3 = 3\uparrow (3\uparrow 3) = 3\uparrow 27 = 3^{3^3} = 3^{27} = 7.625.597.484.987$

$\begin{matrix} 3\uparrow \uparrow \uparrow 3 & = & 3\uparrow \uparrow (3\uparrow \uparrow 3) & = & 3\uparrow \uparrow 7.625.597.484.987 & = & \underbrace{3\uparrow (3\uparrow \ldots\uparrow (3\uparrow 3))} \\ & & & & & & {7.625.597.484.987 \; \mathrm{mal}} \end{matrix}$

$\begin{matrix} G_1 = 3\uparrow \uparrow \uparrow \uparrow 3 & = & 3\uparrow \uparrow \uparrow (3\uparrow \uparrow \uparrow 3) & = & \underbrace{3 \uparrow \uparrow 3 \uparrow \uparrow \ldots \uparrow \uparrow 3} \\ & & & & {3 \uparrow \uparrow \uparrow 3 \; \mathrm{mal}} \end{matrix}$

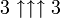Bereits $3\uparrow \uparrow \uparrow 3$ lässt sich nicht mehr vernünftig in der üblichen Exponentialdarstellung (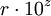$r \cdot 10^z$) oder als Potenzturm ausdrücken. Dazu wäre bereits ein Potenzturm mit 7.625.597.484.987 Exponenten erforderlich. Dennoch kann man die letzten Stellen von Grahams Zahl G₆₄ mit elementarer Zahlentheorie bestimmen. Die letzten 10 Stellen sind 2464195387.

Laut Guinness-Buch der Rekorde ist sie die größte jemals in einem mathematischen Beweis verwendete Zahl. Genauer müsste es „in einem sinnvollen mathematischen Beweis“ lauten, denn ansonsten könnte jemand den mathematischen Satz „Es gilt G₆₅ > G₆₄“ formulieren und einen einfachen Beweis dafür liefern.

Siehe auch

• Liste besonderer Zahlen

Weblinks

• Beitrag bei MathWorld
• Ronald Grahams Homepage
• Grahams Zahl auf Susan Stepneys Homepage
• A Ramsey Problem on Hypercubes von Geoff Exoo