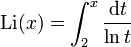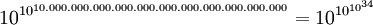Skewes' Zahl

Die Skewes-Zahl (nach Stanley Skewes) ist eine obere Grenze für das Problem der überschätzten Primzahldichte. Ihr genauer Wert beträgt 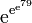$\mathrm e^{ \mathrm e^{ \mathrm e^{79} } }$. Auch die Approximation 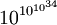$10^{10^{10^{34}} }$ ist gebräuchlich.

Geschichte

Das Problem der überschätzten Primzahldichte basiert auf einer Formel über die Verteilung der Primzahlen, die Carl Friedrich Gauß bereits im Alter von 14 Jahren aufgestellt haben soll (er veröffentlichte sie aber wesentlich später). Demnach kann π(x), die Anzahl der Primzahlen bis x, durch die Formel

$\mathrm{Li}(x) = \int_2^x \frac{\mathrm{d}t}{\ln t}$

angenähert werden. Vergleicht man Li(x) mit konkreten Werten von π(x), die man anhand von Primzahltabellen ermittelt, so ist stets Li(x) > π(x), und man glaubte lange, dies gelte für alle Zahlen bis ins Unendliche.

Im Jahr 1914 bewies J. E. Littlewood, dass die Differenz Li(x) − π(x) bei größer werdendem x das Vorzeichen unendlich oft ändert. Die Gaußsche Formel unterschätzt also die Anzahl der Primzahlen in einem hinreichend großen Zahlenbereich .

1933 gab Stanley Skewes mit der Zahl

$10^{10^{10.000.000.000.000.000.000.000.000.000.000.000}} = 10^{10^ { 10^{34}} }$

eine erste konkrete Abschätzung für die Obergrenze, unterhalb der diese Unterschätzung erstmalig auftreten würde.

Diese Zahl liegt jenseits aller Vorstellungskraft. G. H. Hardy nannte die Skewes-Zahl „die größte Zahl, die je einem bestimmten Zweck in der Mathematik gedient hat“. Spielte man Schach mit allen Teilchen des Universums (≈10⁷⁸), so rechnete Hardy vor, entspräche die Zahl der möglichen Züge in etwa Skewes' Zahl.

Im Jahr 1971 wurde sie von der Graham-Zahl von Platz eins verdrängt. Dies war jedoch lange nach Hardys Tod.

Inzwischen konnte gezeigt werden, dass die Obergrenze für die erste auftretende Unterschätzung unterhalb von ca. 10³⁷¹ liegen muss.

Siehe auch

• Exponentialdarstellung
• Potenzturm
• Liste besonderer Zahlen

Weblinks

• http://mathworld.wolfram.com/SkewesNumber.html