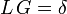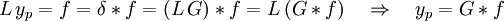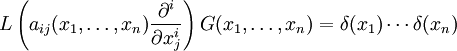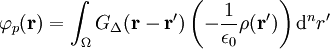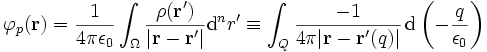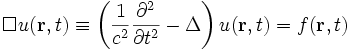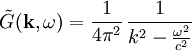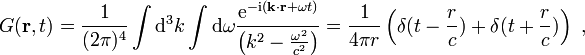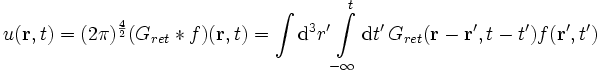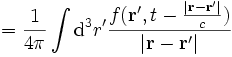Greensfunktion

Eine Greensche Funktion (nach dem Physiker und Mathematiker George Green) ist ein Hilfsmittel bei der Lösung inhomogener linearer Differentialgleichungen. Man sagt, eine Greensche Funktion „propagiert die Inhomogenität“. In der Potentialtheorie und Schweremessung wird sie u. a. zur Lösung des Ersten Randwertproblems eingesetzt. Siehe auch Fundamentallösung und Übertragungsfunktion.

In der Theoretischen Physik, besonders in der Hochenergie- und Vielteilchenphysik, wird ferner eine Fülle verschiedener Funktionen definiert, die allesamt als „Greensche Funktionen“ bezeichnet werden und mit den hier angegebenen Funktionen in der einen oder anderen Form verwandt sind, ohne dass dies auf den ersten Blick erkennbar wäre. Diese Funktionen sind im Folgenden nicht gemeint.

Motivation

Eine inhomogene lineare Differentialgleichung hat die Form

$L\, y = f$,

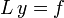wobei L ein linearer Differentialoperator ist. Ziel ist, die partikuläre Lösung y_p zur Inhomogenität f zu finden. Man würde jetzt gerne so etwas wie einen „Umkehr-Operator“ L ^{− 1} finden, denn dann könnte man die Lösung der obigen Gleichung als y = L ^{− 1}f schreiben. Da Ly = 0 aber nicht-triviale Lösungen hat, ist L nicht injektiv, es kann also kein Linksinverses geben. Wohl aber ist L surjektiv, wenn die Gleichung für jedes f Lösungen hat. In diesem Fall hat man also nach einem Rechtsinversen G zu suchen, für das gilt:

Die Greensche Funktion G ist die partikuläre Lösung für die Delta-Distribution δ als Inhomogenität:

$L\, G=\delta$

Nun ist die Frage, wie y_p für eine allgemeine Inhomogenität f aus der Greenschen Funktion G gewonnen werden kann:

$L\,y_{p}=f=\delta*f=(L\,G)*f=L\,(G*f)\quad\Rightarrow\quad y_{p}=G*f$

Erklärung der einzelnen Schritte: Das erste Gleichheitszeichen ist die Ausgangsgleichung Ly_p = f. Für jede Funktion f ist die Faltung mit der Delta-Distribution δ möglich und liefert wieder die Funktion (δ ist das neutrale Element der Faltung): f = δ * f. Verwende δ = LG, also dass G die Differentialgleichung mit δ-Inhomogenität löst. Bildet man die Ableitung einer Faltung, so wird die Ableitung einfach hineingezogen: L(f * g) = (Lf) * g = f * (Lg). Schließlich kann aus Ly_p = L(G * f), die partikuläre Lösung identifiziert werden, nämlich als Faltung der Greenschen Funktion mit der Inhomogenität.

Die allgemeine Lösung ergibt sich durch Addition der allgemeinen Lösung des homogenen Problems mit der partikulären Lösung.

Definition

Gewöhnliche Differentialgleichungen

Sei 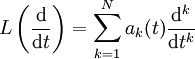$L\left(\frac{\mathrm{d}}{\mathrm{d} t}\right) = \sum_{k=1}^N a_k(t)\frac{\mathrm{d}^k}{\mathrm{d} t^k}$ ein Differentialoperator mit 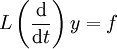$L\left(\frac{\mathrm{d}}{\mathrm{d} t}\right) y = f$. Dann erfüllt eine Greensche Funktion G zu diesem Operator die grundlegende Gleichung:

$L\left(\frac{\mathrm{d}}{\mathrm{d} t}\right) G(t) = \delta(t)$,

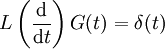wobei δ(t) die Delta-Distribution ist. Unter Umständen fügt man später noch Zusatzbedingungen hinzu, z. B. Retardierungsbedingungen (s.u.) oder die dazu äquivalente „Sommerfeldsche Ausstrahlungsbedingung“ oder eine Anfang- bzw. Randbedingung, durch die G eindeutig wird. Eine spezielle Lösung ergibt sich jedenfalls durch Faltung:

$y(t) = (2\pi)^{\frac{1}{2}}(G * f)(t) \equiv \int_{-\infty}^{\infty} G(t-t')f(t')\mathrm{d}t'$,

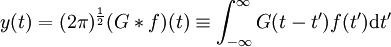wie man wie folgt einsieht:

$L y(t) = \int_{-\infty}^{\infty} L G(t-t') f(t') \mathrm{d}t' = \int_{-\infty}^{\infty} \delta(t-t') f(t') \mathrm{d}t' = f(t).$.

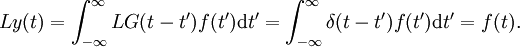Bleibt die Frage, wie man eine Greensche Funktion findet. Im Spezialfall einer Differentialgleichung mit konstanten Koeffizienten ergibt sich, da man Funktionen mit ihren Fourier-Transformierten identifizieren kann, aus dem Faltungstheorem ($\tilde{(f * g)} = \tilde f \tilde g$):

$\frac{1}{\sqrt{2\pi}}\int_{-\infty}^{\infty} \tilde{f}(\omega) \mathrm{e}^{-\mathrm{i} \omega{t} } \mathrm{d} \omega = f(t) = L\left(\frac{\mathrm{d}}{\mathrm{d} t}\right) y(t) = L\left(\frac{\mathrm{d}}{\mathrm{d} t}\right) \frac{1}{\sqrt{2\pi}}\int_{-\infty}^{\infty} \tilde{y}(\omega) \mathrm{e}^{-\mathrm{i}\omega{t} } \mathrm{d} \omega$

$= \frac{1}{\sqrt{2\pi}}\int_{-\infty}^{\infty} L(-\mathrm{i} \omega) \tilde{y}(\omega) \mathrm{e}^{-\mathrm{i}\omega{t} } \mathrm{d} \omega$,

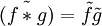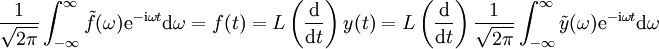
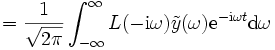bzw. mit der Transferfunktion $Y(-\mathrm{i} \omega ) = \frac{1}{L(- \mathrm{i} \omega )}$:

$\tilde y = Y(- \mathrm{i} \omega ) \tilde f$,

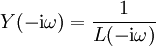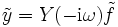und damit, da zudem auch $\tilde{y} = (2\pi)^{\frac{1}{2}}\tilde{G} \tilde{f}$:

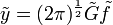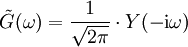$\tilde{G}(\omega ) = \frac{1}{\sqrt{2\pi}}\cdot Y(- \mathrm{i} \omega )$  bzw. $G(t) = \frac{1}{2\pi}\int_{-\infty}^{\infty} Y(- \mathrm{i} \omega ) \mathrm{e}^{-\mathrm{i}\omega{t} } \mathrm{d} \omega$.

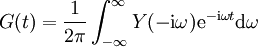Für N=2 entspricht das der stationären („eingeschwungenen“) Antwort des Systems, eines gedämpften harmonischen Oszillators, auf einen ballistischen Einheitsstoß, d.h. auf die spezielle reduzierte Antriebskraft $f(t)=\delta(t)\equiv \frac{1}{2\pi} \,\int\limits_{-\infty}^\infty e^{-\mathrm i\omega t}\mathrm d\omega$.

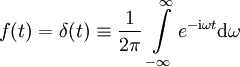Partielle Differentialgleichungen

Für partielle Differentialgleichungen gilt ebenso die definierende Gleichung

$L\left(a_{ij}(x_1,\ldots,x_n) \frac{\partial^{i}}{\partial x_j^{i}}\right)G(x_1,\ldots,x_n)=\delta(x_1)\cdots\delta(x_n)$

und eine spezielle Lösung ergibt sich wiederum durch Faltung:

$y=(2\pi)^{\frac{n}{2}}(G*f)(x_1,\ldots,x_n)$.

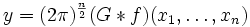Problematischer sind in dem Fall jedoch das Auffinden einer Greenschen Funktion und die Berechnung der mehrdimensionalen Integrale.

Greensche Funktion mit Randbedingungen

Kennt man eine Greensche Funktion zu einem Operator L, so kann man den inhomogenen Teil der Differentialgleichung ohne Probleme lösen. Für die allgemeine Lösung hat man aber im Allgemeinen noch Randbedingungen zu erfüllen. Dies kann auf vielfache Art geschehen, ein elegantes Verfahren ist aber die Addition einer Lösung des homogenen Problems LF = 0, sodass die Randbedingungen erfüllt sind. Anschaulich entspricht dies beim Lösen der Poisson-Gleichung dem Hinzufügen von Bildladungen und Entfernen der Ränder, so dass da, wo der Rand war, die vorher vorgegebenen Werte angenommen werden. Man denke sich als einfaches Beispiel ein geladenes Teilchen vor einer geerdeten Ebene. Bringt man auf der anderen Seite der Ebene eine entgegengesetzt geladene Ladung an und entfernt gedanklich die Ebene, so ist dort, wo die Ebene war, das Potential Null, was die geforderte Randbedingung erfüllt.

Häufig verwendet man dieses Verfahren zum Lösen der Poisson-Gleichung ΔΦ = − 4πρ. Mithilfe des Gaußschen Satzes findet man (G' = G + F):

$\Phi(\mathbf{r}) = \int_\Omega \delta(\mathbf{r}-\mathbf{r}')\Phi(\mathbf{r}') \mathrm{d}^3 r' = \int_\Omega (\nabla\cdot\nabla G'(\mathbf{r}-\mathbf{r}'))\Phi(\mathbf{r}') \mathrm{d}^3 r'$

$= \int_{\partial \Omega} \Phi(\mathbf{r}') \nabla G'(\mathbf{r}-\mathbf{r}') \cdot \mathrm{d}\mathbf{f}\, -\, \int_{\partial\Omega} G'(\mathbf{r}-\mathbf{r}') \nabla \Phi(\mathbf{r}') \cdot \mathrm{d}\mathbf{f}\, +\, \int_\Omega G'(\mathbf{r}-\mathbf{r}') (-4\pi\rho(\mathbf{r}')) \mathrm{d}^3 r'$.

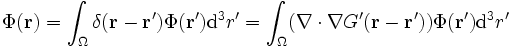
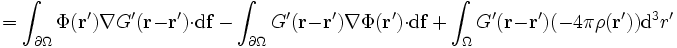Je nachdem, ob man nun das Potential oder dessen Ableitung auf dem Rand vorgegeben hat, wählt man nun die Funktion F die zu G hinzuaddiert werden soll so, dass im ersten Fall 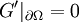$G'|_{\partial\Omega} =0$ gilt und nennt G' üblicherweise Dirichletsche Greensche Funktion G_D. Im zweiten Fall wählt man F nicht wie nahe liegen würde so, dass 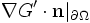$\nabla G' \cdot \mathbf{n}|_{\partial\Omega}$ verschwindet, da dies den Gaußschen Satz verletzen würde. Stattdessen wählt man F so, dass 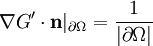$\nabla G' \cdot \mathbf{n}|_{\partial\Omega}= \frac{1}{|\partial\Omega|}$ gilt (was in obigem Integral nur den Mittelwert des Potentials über die Oberfläche produziert, eine Konstante um die die Lösung sowieso unbestimmt ist) und nennt G' üblicherweise Neumannsche Greensche Funktion G_N. Die zu bestimmenden Greenschen Funktionen findet man bei symmetrischen Problemen oft aus geometrischen Überlegungen. Alternativ kann man F nach einem Orthonormalssystems des Operators entwickeln. Hat man eine Lösung gefunden, so ist diese eindeutig bestimmt, wie unmittelbar aus dem Maximumprinzip für elliptische Differentialgleichungen folgt.

Beispiele

Bestimmung des statischen elektrischen Feldes

Nach den Maxwell-Gleichungen gilt für die Quellstärke des zeitlich unveränderlichen elektrischen Feldes

$\mathbf{\nabla} \cdot \mathbf{E}(\mathbf{r}) = \frac{1}{\epsilon_0}\rho(\mathbf{r})$,

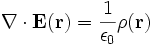wobei 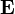$\mathbf{E}$ die elektrische Feldstärke und ρ die elektrische Ladungsdichte ist. Da es sich im elektrostatischen Fall um ein konservatives System handelt, gilt

$\mathbf{E} = -\mathbf{\nabla}\,\varphi$,

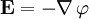wobei $\varphi$ das elektrische Potential ist. Einsetzen liefert die Poisson-Gleichung

$\Delta \varphi = -\frac{1}{\epsilon_0}\rho(\mathbf{r})$,

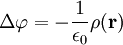also eine inhomogene lineare partielle Differentialgleichung 2. Ordnung. Kennt man eine Greensche Funktion des Laplace-Operators 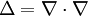$\Delta = \mathbf{\nabla} \cdot \mathbf{\nabla}$, so lautet eine partikuläre Lösung

$\varphi_p(\mathbf{r}) = \int_\Omega G_\Delta(\mathbf{r} - \mathbf{r}')\left( -\frac{1}{\epsilon_0}\rho(\mathbf{r}')\right) \mathrm{d}^n r'$

Eine (nicht eindeutig bestimmte) Greensche Funktion des Laplace Operators ist

$G_\Delta(\mathbf{r}) = - \frac{1}{4\pi}\frac{1}{|\mathbf{r}|}$,

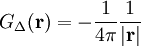womit sich nach Einsetzen

$\varphi_p(\mathbf{r}) = \frac{1}{4\pi\epsilon_0}\int_\Omega \frac{\rho(\mathbf{r}')}{|\mathbf{r}-\mathbf{r}'|}\mathrm{d}^n r' \equiv \int_Q \frac{-1}{4\pi|\mathbf{r}-\mathbf{r}'(q)|}\,\mathrm{d}\left( -\frac{q}{\epsilon_0}\right)$

ergibt. Letzte Gleichung soll die physikalische Interpretation der Greenschen Funktion verdeutlichen. Die Greensche Funktion zusammen mit dem Differential stellen einen „Potentialstoß“ dar, das Gesamtpotential ergibt sich dann durch Superposition aller „Potentialstöße“, also durch Ausführen des Integrals.

Inhomogene Wellengleichung

Dieser Fall ist etwas schwieriger und anders geartet, weil man es nicht mit einer elliptischen, sondern mit einer hyperbolischen Differentialgleichung zu tun hat. Hier treten die oben angedeuteten Komplikationen auf.

Die inhomogene Wellengleichung hat die Form

$\Box u(\mathbf{r},t) \equiv \left( \frac{1}{c^2}\frac{\partial^2}{\partial t^2} - \Delta \right) u(\mathbf{r},t) = f(\mathbf{r},t)$

Durch Fourier-Zerlegung findet man nach Ausführen des Operators für die Fourier-Transformierten

$\left(k^2 -\frac{\omega^2}{c^2} \right)\tilde{u}(\mathbf{k},\omega) = \tilde f(\mathbf{k},\omega)$.

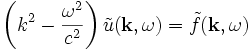Nach dem Faltungstheorem gilt also:

$\tilde G(\mathbf{k},\omega) = \frac{1}{4\pi^2}\,\frac{1}{k^2-\frac{\omega^2}{c^2}}$

Die Rücktransformation kann man mithilfe des Residuenkalküls ausrechnen und findet

$G(\mathbf{r},t) = \frac{1}{(2\pi)^4} \int \mathrm{d}^3 k \int \mathrm{d} \omega \frac{ \mathrm{e}^{-\mathrm{i} ( \mathbf{k} \cdot \mathbf{r} + \omega t) }} {\left( k^2 - \frac{\omega^2}{c^2}\right)} = \frac{1}{4\pi r}\left( \delta(t-\frac{r}{c}) + \delta(t + \frac{r}{c})\right)\,\,,$

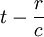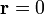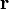was in natürlicher Weise zu zwei Anteilen („retardierter“ bzw. „avancierter“ Anteil) der Greenschen Funktion Anlass gibt. Das Argument in der ersten Deltafunktion, $t-\frac{r}{c}$, bedeutet nämlich, dass eine zum Zeitpunkt t = 0 bei $\mathbf r=0$ erzeugte „Ursache“ durch die endliche Ausbreitungsgeschwindigkeit der Welle erst zum Zeitpunkt $\frac{r}{c}$ ihre „Wirkung“ am Ort $\mathbf{r}$ hervorruft. Für die zweite Deltafunktion ergibt sich, dass die Wirkung gegenüber der Ursache um das entsprechende Zeitintervall voraneilt. Aus Kausalitätsgründen ist das unmöglich; d.h., die avancierte Greensche Funktion muss als unphysikalisch angesehen werden. Die retardierte Lösung der Wellengleichung ergibt sich dann durch Faltung:

$u(\mathbf{r},t) = (2\pi)^{\frac{4}{2}} (G_{ret}*f)(\mathbf{r},t) = \int \mathrm{d}^3 r' \int\limits_{-\infty}^t\mathrm{d}t'\, G_{ret}(\mathbf{r}-\mathbf{r}',t-t')f(\mathbf{r}',t')$

$= \frac{1}{4\pi} \int \mathrm{d}^3 r' \frac{f(\mathbf{r}',t-\frac{|\mathbf{r}-\mathbf{r}'|}{c})}{|\mathbf{r}-\mathbf{r}'|}$

Es gilt also ein Superpositionsprinzip mit Retardierung: Die Lösung ist eine Überlagerung von auslaufenden Kugelwellen (Huygenssches Prinzip, Sommerfeldsche Ausstrahlungsbedingung), deren Bildung ähnlich wie in der Elektrostatik erfolgt.

Bemerkungen

Die obige Darstellung ist für gewöhnliche Funktionen mathematisch nicht streng, z. B. darf man sicher nicht immer Integral- und Differentialoperator vertauschen. Es ist auf der Ebene eines Kalküls argumentiert worden. Der Kalkül der Dirac-Distribution ist jedoch einfach zu merken und führt in vielen Fällen auf die richtige Fährte, weswegen Physiker und Ingenieure häufig so verfahren. Wenn man wirklich verstehen will, was man eigentlich macht, muss man sich mit der Distributionstheorie auseinandersetzen und sog. Verallgemeinerte Funktionen betrachten.

Weblinks

• Greensche Funktion bei MathWorld (englisch)