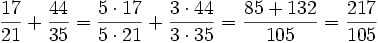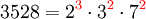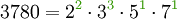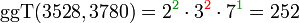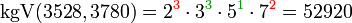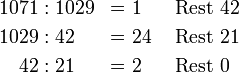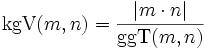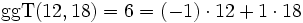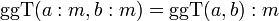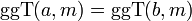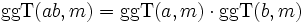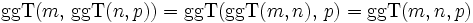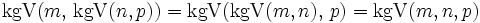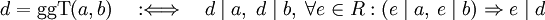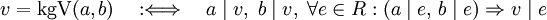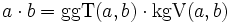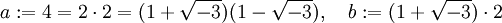- Größter Gemeinsamer Teiler
-
Der größte gemeinsame Teiler (ggT) und das kleinste gemeinsame Vielfache (kgV) sind zwei zusammengehörende mathematische Begriffe. Sie spielen unter anderem in der Bruchrechnung und der Zahlentheorie eine Rolle.
Der größte gemeinsame Teiler zweier ganzer Zahlen m und n ist die größte natürliche Zahl, durch die sowohl m als auch n ohne Rest teilbar sind. Für m = n = 0 ist der größte gemeinsame Teiler nicht definiert; für die algebraische Definition gelten abweichende Eigenschaften.
Das kleinste gemeinsame Vielfache zweier ganzer Zahlen m und n ist die kleinste natürliche Zahl, die sowohl Vielfaches von m als auch Vielfaches von n ist.
Inhaltsverzeichnis
Beispiele
Hier werden der Einfachheit halber nur natürliche Zahlen betrachtet.
Größter gemeinsamer Teiler:
12 ist durch die folgenden Zahlen ohne Rest teilbar: 1, 2, 3, 4, 6, 12.
18 hat diese Teiler: 1, 2, 3, 6, 9, 18.
Die gemeinsamen Teiler von 12 und 18 sind also 1, 2, 3, 6 und der größte von diesen ist 6; in Zeichen: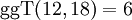 .
.
Kleinstes gemeinsames Vielfaches:
Die Vielfachen von 12 sind: 12, 24, 36, 48, 60, 72, 84, …
Die Vielfachen von 18 sind: 18, 36, 54, 72, 90, 108, …
Die gemeinsamen Vielfachen von 12 und 18 sind also 36, 72, 108, … und das kleinste von diesen ist 36; in Zeichen: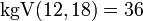 .
.
Anwendungen in der Bruchrechnung
Kürzen:
Beim Kürzen wird ein gemeinsamer Faktor von Zähler und Nenner eines Bruches entfernt, wobei sich der Wert des Bruches nicht ändert, z. B.
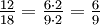 . Kürzt man mit dem größten gemeinsamen Teiler von Zähler und Nenner, entsteht ein Bruch, der nicht weiter kürzbar ist. Zum Beispiel ist
. Kürzt man mit dem größten gemeinsamen Teiler von Zähler und Nenner, entsteht ein Bruch, der nicht weiter kürzbar ist. Zum Beispiel ist 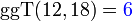 , also
, also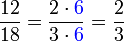 .
.
Hauptnenner:
Angenommen, wir möchten die Brüche
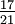 und
und 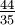 addieren. Dazu müssen diese durch Erweitern auf einen gemeinsamen Nenner gebracht werden. Man könnte natürlich einfach 21 mit 35 multiplizieren, was 735 ergibt. Der kleinstmögliche gemeinsame Nenner (der sog. Hauptnenner) ist aber
addieren. Dazu müssen diese durch Erweitern auf einen gemeinsamen Nenner gebracht werden. Man könnte natürlich einfach 21 mit 35 multiplizieren, was 735 ergibt. Der kleinstmögliche gemeinsame Nenner (der sog. Hauptnenner) ist aber 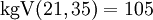 . Die beiden Brüche werden auf diesen Nenner erweitert und dann addiert:
. Die beiden Brüche werden auf diesen Nenner erweitert und dann addiert:Berechnung
Berechnung über die Primfaktorzerlegung
GgT und kgV kann man über die Primfaktorzerlegung der beiden gegebenen Zahlen bestimmen. Beispiel:
Für den ggT nimmt man die Primfaktoren, die in beiden Zerlegungen vorkommen, und als zugehörigen Exponenten den jeweils kleineren der Ausgangsexponenten:
Für das kgV nimmt man die Primfaktoren, die in mindestens einer der beiden Zerlegungen vorkommen, und als zugehörigen Exponenten den jeweils größeren der Ausgangsexponenten:
Euklidischer und steinscher Algorithmus
Die Berechnung der Primfaktorzerlegung großer Zahlen und damit auch die Bestimmung des größten gemeinsamen Teilers nach obiger Methode ist sehr aufwändig. Mit dem euklidischen Algorithmus existiert jedoch ein effizientes Verfahren, um den größten gemeinsamen Teiler zweier Zahlen zu berechnen. Dieses Verfahren wird durch den steinschen Algorithmus noch weiter verbessert.
Beim euklidischen Algorithmus wird in aufeinanderfolgenden Schritten jeweils eine Division mit Rest durchgeführt, wobei der Rest im nächsten Schritt zum neuen Divisor wird. Der Divisor, bei dem sich Rest 0 ergibt, ist der größte gemeinsame Teiler der Ausgangszahlen. Beispiel:
Somit ist 21 der größte gemeinsame Teiler von 1071 und 1029.
Zusammenhang von ggT und kgV
Es gilt die folgende Formel (wobei der Fall m = n = 0 ausgeschlossen ist):
Damit lässt sich das kgV berechnen, falls der ggT (z. B. mit dem euklidischen Algorithmus) bereits bestimmt wurde. Umgekehrt kann man mit dieser Formel auch den ggT aus dem kgV berechnen.
Lemma von Bézout
→ Hauptartikel: Lemma von Bézout
Nach dem Lemma von Bézout lässt sich der größte gemeinsame Teiler zweier ganzer Zahlen m und n als Linearkombination von m und n mit ganzzahligen Koeffizienten darstellen:
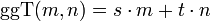 mit
mit 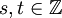
Beispielsweise besitzt der größte gemeinsame Teiler von 12 und 18 die folgende Darstellung:
Die Koeffizienten s und t können mit dem erweiterten euklidischen Algorithmus berechnet werden.
Rechenregeln für den ggT
a und b seien ganze Zahlen und m eine natürliche Zahl. Dann gilt:
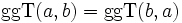 (Kommutativgesetz)
(Kommutativgesetz)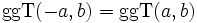
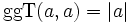
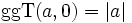
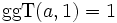
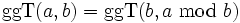 (b > 0)
(b > 0)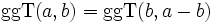
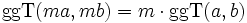 (Distributivgesetz)
(Distributivgesetz)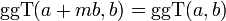
Ist m ein gemeinsamer Teiler von a und b, dann gilt:
Ist
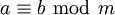 (a und b sind kongruent modulo m), dann gilt:
(a und b sind kongruent modulo m), dann gilt:Hält man eines der beiden Argumente fest, dann ist
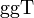 eine multiplikative Funktion, denn für teilerfremde Zahlen a und b gilt
eine multiplikative Funktion, denn für teilerfremde Zahlen a und b giltBerechnung des ggT und des kgV von mehreren Zahlen
Der
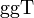 und das
und das 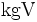 lassen sich von beliebig vielen Zahlen berechnen, da beide Abbildungen assoziativ sind:
lassen sich von beliebig vielen Zahlen berechnen, da beide Abbildungen assoziativ sind:GgT und kgV in weiteren algebraischen Strukturen
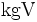 und
und 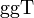 lassen sich nicht nur für natürliche (und ganze) Zahlen definieren. Man kann sie z. B. auch für Polynome bilden. Statt der Primzahlzerlegung nimmt man hier die Zerlegung in irreduzible Faktoren:
lassen sich nicht nur für natürliche (und ganze) Zahlen definieren. Man kann sie z. B. auch für Polynome bilden. Statt der Primzahlzerlegung nimmt man hier die Zerlegung in irreduzible Faktoren:- f(x) = x2 + 2xy + y2 = (x + y)2
- g(x) = x2 − y2 = (x + y)(x − y)
Dann ist
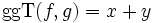 und
und 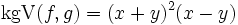 .
.Möglich wird dies, da auch für Polynome eine Division mit Rest existiert.
Um den Begriff des größten gemeinsamen Teilers auf beliebige kommutative Ringe ausdehnen zu können, muss man die Definition ändern, da in beliebigen Ringen nicht vorausgesetzt werden kann, dass die Elemente bezüglich < angeordnet werden können. Deshalb ersetzt man diese Anordnung durch die durch den Teilbarkeitsbegriff definierte partielle Ordnung.
Ist d ein Ringelement, das sowohl Teiler von a als auch Teiler von b ist, dann heißt d ein gemeinsamer Teiler von a und b. Gilt zusätzlich, dass jeder weitere gemeinsame Teiler von a und b auch ein Teiler von d ist, dann heißt d ein größter gemeinsamer Teiler von a und b.
Analog ist das
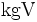 definiert: Ein Ringelement v heißt kleinstes gemeinsames Vielfaches zweier Ringelemente a und b, wenn v ein gemeinsames Vielfaches von a und b ist und seinerseits jedes andere gemeinsame Vielfache von a und b ein Vielfaches von v ist.
definiert: Ein Ringelement v heißt kleinstes gemeinsames Vielfaches zweier Ringelemente a und b, wenn v ein gemeinsames Vielfaches von a und b ist und seinerseits jedes andere gemeinsame Vielfache von a und b ein Vielfaches von v ist.Formal schreibt man diese Definition für einen Ring R so:
Diese allgemeinere Definition lässt sich auf mehrere Zahlen ausweiten (sogar auf unendlich viele).
Beispiel: Im gaußschen Zahlenring
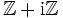 ist der größte gemeinsame Teiler von 2 und 1 + 3i gerade 1 + i, denn 2 = − i(1 + i)2 und 1 + 3i = (1 + i)(2 + i). Genau genommen ist 1 + i ein größter gemeinsamer Teiler, da alle zu dieser Zahl assoziierten Zahlen ebenfalls größte gemeinsame Teiler sind.
ist der größte gemeinsame Teiler von 2 und 1 + 3i gerade 1 + i, denn 2 = − i(1 + i)2 und 1 + 3i = (1 + i)(2 + i). Genau genommen ist 1 + i ein größter gemeinsamer Teiler, da alle zu dieser Zahl assoziierten Zahlen ebenfalls größte gemeinsame Teiler sind.Nicht in jedem Ring existiert für zwei Elemente ein
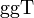 oder ein
oder ein 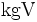 . Wenn sie einen
. Wenn sie einen 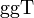 haben, können sie mehrere
haben, können sie mehrere 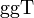 ’s haben. Ist der Ring ein Integritätsring, dann sind alle
’s haben. Ist der Ring ein Integritätsring, dann sind alle 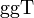 ’s zueinander assoziiert.
’s zueinander assoziiert.Ist R ein Integritätsring und haben die Elemente a und b ein
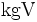 , dann haben sie auch einen
, dann haben sie auch einen 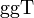 , und es gilt die Gleichung
, und es gilt die GleichungIst jedoch nur bekannt, dass ein
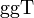 von a und b existiert, dann muss nicht unbedingt auch ein
von a und b existiert, dann muss nicht unbedingt auch ein 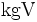 existieren.
existieren.Beispiel
Im Integritätsring
![R = \mathbb{Z}[\sqrt{-3}]](/pictures/dewiki/50/2a4da41eac48f1d91b11c65f63ed4563.png) haben die Elemente
haben die Elementekeinen
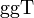 : Die Elemente
: Die Elemente 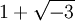 und 2 sind zwei maximale gemeinsame Teiler (denn beide haben den gleichen Betrag), aber diese zwei Elemente sind nicht zueinander assoziiert, also gibt es keinen
und 2 sind zwei maximale gemeinsame Teiler (denn beide haben den gleichen Betrag), aber diese zwei Elemente sind nicht zueinander assoziiert, also gibt es keinen 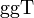 von a und b.
von a und b.Die genannten Elemente
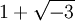 und 2 haben aber ihrerseits einen
und 2 haben aber ihrerseits einen 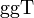 , nämlich 1. Dagegen haben sie kein
, nämlich 1. Dagegen haben sie kein 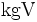 , denn wenn v ein
, denn wenn v ein 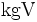 wäre, dann folgt aus der „
wäre, dann folgt aus der „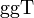 -
-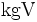 -Gleichung“, dass v assoziiert zu
-Gleichung“, dass v assoziiert zu 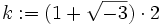 sein muss. Das gemeinsame Vielfache 4 ist jedoch kein Vielfaches von k, also ist k kein
sein muss. Das gemeinsame Vielfache 4 ist jedoch kein Vielfaches von k, also ist k kein 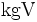 und die beiden Elemente haben gar kein
und die beiden Elemente haben gar kein 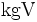 .
.Ein Integritätsring, in dem je zwei Elemente einen
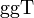 besitzen, heißt
besitzen, heißt 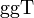 -Ring oder
-Ring oder 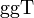 -Bereich.
-Bereich.In einem
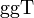 -Ring haben je zwei Elemente auch ein
-Ring haben je zwei Elemente auch ein 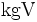 .
.In einem faktoriellen Ring haben je zwei Elemente einen
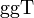 .
.In einem euklidischen Ring lässt sich der
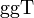 zweier Elemente mit dem euklidischen Algorithmus bestimmen.
zweier Elemente mit dem euklidischen Algorithmus bestimmen.Alternative Notationen
Die englischen Bezeichnungen gcd (greatest common divisor) für ggT und lcm (least common multiple) für kgV sind in mathematischen Texten ebenfalls verbreitet.
Oft wird auch
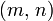 als Kurzschreibweise für
als Kurzschreibweise für 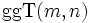 verwendet.
verwendet.Weblinks
- Online-Tool zur Berechnung des ggT und des kgV von zwei oder drei Zahlen
- Verschiedene Online-Tools zur Primfaktorzerlegung, ggT und kgV.
- Online-Tool zur Berechnung des ggT zweier Zahlen
Wikimedia Foundation.