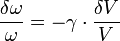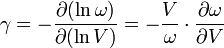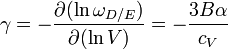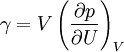Grüneisenparameter

Der Grüneisen-Parameter γ (nach Eduard Grüneisen) beschreibt die Abhängigkeit der Frequenz von Gitterschwingungen (Phononen) in einem Kristall von der relativen Volumenänderung, die ihrerseits von der Temperatur abhängt.

In einem einfachen Modell nimmt man an, dass alle Wechselwirkungen in einem Kristall harmonisch sind. Dies beschreibt reale Festkörper nur unzureichend, da diese z.B. eine Volumenausdehnung mit steigender Temperatur zeigen, was von einem solchen harmonischen Modell nicht berücksichtigt wird. Darum führt man Terme höherer Ordnung in das Wechselwirkungs-Potenzial im Festkörper ein und erhält neue Effekte.

Somit hängt jetzt die relative Schwingungsfrequenzänderung δω/ω eines Phonons bestimmten Impulses und in einem bestimmten Phononenzweig linear von der relativen Volumenausdehnung δ V/V ab:

$\frac{\delta \omega}{\omega}=-\gamma \cdot \frac{\delta V}{V}$

Dabei ist der dimensionslose Grüneisenparameter γ definiert als:

$\gamma=-\frac{\partial(\ln\omega)}{\partial(\ln V)}=-\frac{V}{\omega}\cdot\frac{\partial\omega}{\partial V}$

Typische Werte liegen bei Zimmertemperatur zwischen 1 und 2. Dies bedeutet, dass das Volumen und die Phononenfrequenzen sich etwa gleich stark ändern.

Da der Druck und damit die linear Ausdehnung von Festkörpern über die Abhängigkeit der Normalfrequenzen vom Volumen von der Temperatur abhängen, muss man streng genommen für jede Mode einen eigenen Grüneisenparameter definieren. Allerdings skalieren im Debye/Einstein-Model alle Frequenzen mit der sogenannten Debye/Einstein Frequenz ω_{D / E} und die Grüneisenkonstanten wird identisch für alle Moden:

$\gamma=-\frac{\partial(\ln\omega_{D/E})}{\partial(\ln V)}=-\frac{3B \alpha}{c_V}$

mit B als Bulk Modulus und α dem linearen Ausdehnungskoeffizienten. Dies ist gleichbedeutend mit der Tatsache, dass spezifische Wärme und Ausdehnungskoeffizient eine ähnliche Temperaturabhängigkeit aufweist. Deshalb ist die Definition eines konstanten Grüneisenparameters sinnvoll.

Eine thermodynamische Ableitung des Grüneisenparameters

$\gamma = V \left( \frac{\partial p}{\partial U} \right)_V$

beschreibt die Änderung des Drucks p mit der inneren Energie U bei konstantem Volumen V. Damit wird der Grüneisen-Parameter direkt messbar. Man kann die innere Energie in einem Bereich des Kristall bei konstantem Volumen erhöhen, wenn man zum Beispiel mit einem Laserpuls einstrahlt. Dabei wird eine Druckwelle erzeugt, die man dann an der Kristalloberfläche detektiert.

Siehe auch: Debye-Modell