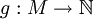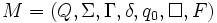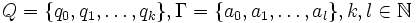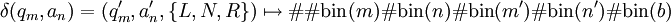- Gödel-Isomorphie
-
Eine Gödelnummer ist eine natürliche Zahl, die einem Wort einer formalen Sprache nach einem gewissermaßen „durchschaubaren“ Verfahren – Gödelisierung – zugeordnet wird und dieses Wort eindeutig kennzeichnet. Alle über die Kodierung von Programmen in einer Programmiersprache definierten Aufzählungen sind Gödelnummerierungen. Die Bezeichnungen beziehen sich auf Kurt Gödel, der erstmals ein solches Verfahren angab, um seinen Unvollständigkeitssatz zu beweisen.
Inhaltsverzeichnis
Formale Definition
Sei M die (abzählbare) Menge der Wörter einer formalen Sprache. Eine Funktion
wird Gödelisierung genannt, wenn[1]
- g injektiv und berechenbar,
- die Bildmenge g(M) entscheidbar sowie
- die auf g(M) definierte Umkehrfunktion von g berechenbar ist.
g(m) nennt man dann die Gödelnummer von m.
Beispiel
Angenommen, beliebige Wörter der formalen Sprache L, die auf dem Alphabet Σ basieren, sollen gödelisiert werden. Hier sei Σ = {a,b,c}.
Eine Möglichkeit der Kodierung wäre, den Buchstaben zunächst einfach fortlaufende Nummern zuzuweisen. Ein „a“ entspräche der 1, ein „b“ der 2 und ein „c“ der 3. Nun kann man gödelisieren, indem man die dem Buchstaben entsprechenden Potenzen der fortlaufenden Primzahlen
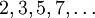 miteinander multipliziert:
miteinander multipliziert:Das Wort „abccba“
- Das „a“ an erster Stelle hat den Wert 21 = 2
- Das „b“ an zweiter Stelle hat den Wert 32 = 9
- Das „c“ an dritter Stelle hat den Wert 53 = 125
- Das „c“ an vierter Stelle hat den Wert 73 = 343
- Das „b“ an fünfter Stelle hat den Wert 112 = 121
- Das „a“ an sechster Stelle hat den Wert 131 = 13
Die Gödelnummer für „abccba“ in dieser Kodierung lautet also
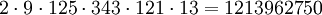
Da es unendlich viele Primzahlen gibt, kann man auf diese Weise tatsächlich beliebig lange Wörter kodieren und aufgrund der Eindeutigkeit der Primfaktorzerlegung lässt sich etwa aus der Zahl 1213962750 wieder das Wort „abccba“ rekonstruieren. Es gibt zwar Zahlen, die keinem Wort der Sprache entsprechen, beispielsweise
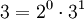 (kein erster Buchstabe) oder 16 = 24 (ergäbe „d“, aber „d“ ist nicht Element des Alphabets Σ). Aber zumindest lassen sich diese ungültigen Werte auf berechenbare Weise von den gültigen unterscheiden.
(kein erster Buchstabe) oder 16 = 24 (ergäbe „d“, aber „d“ ist nicht Element des Alphabets Σ). Aber zumindest lassen sich diese ungültigen Werte auf berechenbare Weise von den gültigen unterscheiden.Neben der hier gezeigten gibt es natürlich noch andere Methoden, eine Gödelisierung durchzuführen.
Eine im Buch Gödel, Escher, Bach beschriebene Methode verwendet beispielsweise ein Stellenwertsystem mit der Basis 1000, was zwar sehr anschaulich ist, aber formal schwieriger zu handhaben ist als eine Methode, die wie die obige auf Primzahlpotenzen beruht.
Gödelisierung von zahlentheoretischen Aussagen
Aussagen der Zahlentheorie (oder auch anderer mathematischer Theorien) lassen sich mit Hilfe eines endlichen Alphabets formulieren, dessen „Buchstaben“ neben Zeichen für Variablen auch gewisse mathematische und logische Symbole (etwa + ,
 , = ,
, = , 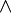 ,
,  ,
, 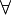 ) umfasst. (Die abzählbar unendlich vielen Variablen können als besonders gekennzeichnete Wörter des endlichen Alphabets dargestellt werden.)
) umfasst. (Die abzählbar unendlich vielen Variablen können als besonders gekennzeichnete Wörter des endlichen Alphabets dargestellt werden.)Auf diese Weise lassen sich also zahlentheoretische Aussagen (und sogar Beweise) in Zahlen übersetzen. Als Folge hiervon kann die Zahlentheorie, die ja Aussagen über Zahlen behandeln soll, auch Aussagen über zahlentheoretische Aussagen und Beweise behandeln. Diese Tatsache ist der Ansatzpunkt, auf dem Gödels Unvollständigkeitssatz beruht.
Gödelisierung von Turingmaschinen
Eine bekannte Anwendung der Gödelnummer ist die Codierung einer Turingmaschine durch ein Binärwort w. Auf diese Weise wird jeder Turingmaschine eine Zahl zugeordnet (d. h. die Menge aller Turingmaschinen ist abzählbar). Diese Tatsache wird unter Anderem im Halteproblem ausgenutzt.
Beispiel
Natürlich lassen sich verschiedenste Konventionen für die Nummerierung vereinbaren. Im Folgenden soll der Vorgang an einem einfachen Beispiel gezeigt werden. Sei
eine Turingmaschine. Seien o. B. d. A. die Zustandsmenge Q, sowie das Bandalphabet Γ durchnummeriert.
Wir codieren nun vorerst jeden Übergang δ(qm,an) = (qm',an',{L,N,R}) mit einem Wort über dem Alphabet
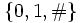 . Zustände bzw. Terminalsymbole werden durch die Binärdarstellung ihrer Indizes dargestellt, die einzelnen Elemente werden mit
. Zustände bzw. Terminalsymbole werden durch die Binärdarstellung ihrer Indizes dargestellt, die einzelnen Elemente werden mit 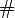 getrennt.
getrennt.wobei b die Kopfbewegung darstellt (L = 0,N = 1,R = 2). Um uns auf das zweistellige Alphabet {0,1} beschränken zu können, führen wir eine Abbildung der Menge
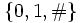 auf {0,1} ein:
auf {0,1} ein: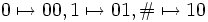 .
.
Die Turingmaschine mit der einzigen Produktion
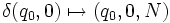 wird so zu 10100010001000100010012 = 265639310.
wird so zu 10100010001000100010012 = 265639310.Eine Alternative, die auf das Trennzeichen verzichtet, nutzt die Eindeutigkeit der Primfaktorzerlegung aus, um Tupel in einer Zahl codieren zu können.
Siehe auch
Einzelnachweis
- ↑ Hans Hermes: Aufzählbarkeit – Entscheidbarkeit – Berechenbarkeit, 2. Auflage. Springer, Berlin 1971; S. 4. ISBN 3-540-05334-4, ISBN 0-387-05334-4
Wikimedia Foundation.