- Mannigfaltigkeitslehre
-
Die Mengenlehre ist ein grundlegendes Teilgebiet der Mathematik. Zahlreiche mathematische Disziplinen werden heute auf der Mengenlehre aufgebaut, darunter die Algebra, Analysis, Maßtheorie, Stochastik und Topologie.
Inhaltsverzeichnis
Geschichte
Mengenlehre im 19. Jahrhundert
Die Mengenlehre begründete Georg Cantor in den Jahren 1874–1897. Statt des Begriffs Menge benutzte er anfangs Wörter wie „Inbegriff“ oder „Mannigfaltigkeit“; von Mengen und Mengenlehre sprach er erst später. 1895 formulierte er folgende Mengendefinition:
- Unter einer „Menge“ verstehen wir jede Zusammenfassung M von bestimmten wohlunterschiedenen Objekten m unserer Anschauung oder unseres Denkens (welche die „Elemente“ von M genannt werden) zu einem Ganzen.[1]
Cantor klassifizierte die Mengen, insbesondere die unendlichen, nach ihrer Mächtigkeit. Für endliche Mengen ist das die Anzahl ihrer Elemente. Er nannte zwei Mengen äquivalent (gleichmächtig), wenn sie sich bijektiv aufeinander abbilden lassen. Die Mächtigkeit oder Kardinalzahl einer Menge M ist nach Cantor die Äquivalenzklasse der zu M äquivalenten (gleichmächtigen) Mengen. Er beobachtete wohl als Erster, dass es verschiedene unendliche Mächtigkeiten gibt. Die Menge der natürlichen Zahlen und alle gleichmächtigen Mengen heißen nach Cantor abzählbar.
Wichtige Ergebnisse von Cantor:
- Die Mengen der natürlichen, der rationalen und der algebraischen Zahlen sind gleichmächtig (Cantors erstes Diagonalargument).
- Die Menge der reellen Zahlen hat größere Mächtigkeit als die der natürlichen Zahlen, ist also nichtabzählbar (Cantors zweites Diagonalargument).
- Die Menge aller Untermengen einer Menge M (ihre Potenzmenge) hat stets größere Mächtigkeit als M (Cantors zweites Diagonalargument verallgemeinert).
- Von je zwei Mengen ist mindestens eine gleichmächtig zu einer Untermenge der anderen. Das wird mit Hilfe der von Cantor ausführlich behandelten Wohlordnung bewiesen.
- Es gibt nichtabzählbar unendlich viele Mächtigkeiten.
Cantor benannte das Kontinuumproblem: Gibt es eine Mächtigkeit zwischen der der natürlichen und der der reellen Zahlen? Er selbst versuchte es zu lösen, blieb aber erfolglos. Später stellte sich heraus, dass die Frage grundsätzlich nicht entscheidbar ist.
Neben Cantor war auch Richard Dedekind ein wichtiger Wegbereiter der Mengenlehre. Er sprach von Systemen statt von Mengen und entwickelte 1872 eine mengentheoretische Konstruktion der reellen Zahlen[2] und 1888 eine verbale mengentheoretische Axiomatisierung der natürlichen Zahlen.[3]
Giuseppe Peano, der Mengen als Klassen bezeichnete, schuf bereits 1889 den ersten formalen Klassenlogik-Kalkül als Basis für seine Arithmetik mit den Peano-Axiomen, die er erstmals in einer präzisen mengentheoretischen Sprache formulierte. Er entwickelte damit die Grundlage für die heutige Formelsprache der Mengenlehre und führte viele heute gebräuchliche Symbole ein, darunter das Symbol ε für das Elementprädikat, das heute als
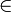 stilisiert und als „ist Element von“ verbalisiert wird.[4]
stilisiert und als „ist Element von“ verbalisiert wird.[4]Eine andere mengentheoretische Begründung der Arithmetik versuchte Gottlob Frege wenig später in seinem Kalkül von 1893. In diesem entdeckte Bertrand Russell 1902 einen Widerspruch, der als Russellsche Antinomie bekannt wurde. Dieser Widerspruch und auch andere Widersprüche entstehen aufgrund einer uneingeschränkten Mengenbildung, weshalb die Frühform der Mengenlehre später als naive Mengenlehre bezeichnet wurde. Cantors Mengendefinition beabsichtigt aber keine solche naive Mengenlehre, wie sein Beweis der Allklasse als Nichtmenge durch die Cantorsche Antinomie belegt.[5]
Cantors Mengenlehre wurde von seinen Zeitgenossen in ihrer Bedeutung kaum erkannt und keineswegs als revolutionärer Fortschritt angesehen, sondern stieß bei manchen Mathematikern, etwa bei Leopold Kronecker, auf Ablehnung. Noch mehr geriet sie in Misskredit, als Antinomien bekannt wurden, so dass etwa Henri Poincaré spottete: „Die Logik ist gar nicht mehr steril – sie zeugt jetzt Widersprüche.“
Mengenlehre im 20. Jahrhundert
Die Mengenlehre im 20. Jahrhundert ist die Geschichte des wachsenden Erfolgs von Cantors Ideen und gleichzeitig der Überwindung der Widersprüche durch fortschreitende Präzisierung als axiomatische Mengenlehre.
1903/1908 entwickelte Bertrand Russell seine Typentheorie, in der Mengen stets einen höheren Typ als ihre Elemente haben, damit problematische Mengenbildungen unmöglich würden. Er wies den ersten Ausweg aus den Widersprüchen und zeigte in den Principia Mathematica von 1910-1913 auch ein Stück der Leistungsfähigkeit der angewandten Typentheorie. Letztlich erwies sie sich aber als unzulänglich für Cantors Mengenlehre und konnte sich auch wegen ihrer Kompliziertheit nicht durchsetzen.
Handlicher und erfolgreicher war dagegen die von Ernst Zermelo 1907 entwickelte axiomatische Mengenlehre, die er gezielt zur widerspruchsfreien Begründung der Mengenlehre von Cantor und Dedekind schuf. Abraham Fraenkel bemerkte 1921, dass dazu zusätzlich sein Ersetzungsaxiom nötig ist. Zermelo fügte es in sein Zermelo-Fraenkel-System von 1930 ein, das er kurz ZF-System nannte. Er konzipierte es auch für Urelemente, die keine Mengen sind, aber als Mengenelemente in Frage kommen und Cantors „Objekte unserer Anschauung“ einkalkulieren. Die heutige Zermelo-Fraenkel-Mengenlehre ist dagegen nach Fraenkels Vorstellung eine reine Mengenlehre, deren Objekte ausschließlich Mengen sind.
Viele Mathematiker setzten aber statt auf eine konsequente Axiomatisierung auf eine pragmatische Mengenlehre, die Problem-Mengen mied, so etwa die oft aufgelegten Mengenlehren von Felix Hausdorff ab 1914 oder von Erich Kamke ab 1928. Nach und nach wurde es immer mehr Mathematikern bewusst, dass die Mengenlehre eine unentbehrliche Grundlage für die Strukturierung der Mathematik ist. Das ZF-System bewährte sich in der Praxis, weshalb es heute als Basis der modernen Mathematik von der Mehrheit der Mathematiker anerkannt ist. Keinerlei Widersprüche konnten mehr abgeleitet werden. Die Widerspruchsfreiheit konnte allerdings nur für die Mengenlehre mit endlichen Mengen nachgewiesen werden, aber nicht für das komplette ZF-System, das Cantors Mengenlehre mit unendlichen Mengen enthält, und zwar wegen Gödels Unvollständigkeitssatz von 1931. Gödels Entdeckungen steckten nur Hilberts Programm, die Mathematik und Mengenlehre auf eine nachweislich widerspruchsfreie axiomatische Basis zu stellen, eine Grenze, aber hinderten den Erfolg der Mengenlehre in keiner Weise, so dass von einer Grundlagenkrise der Mathematik, von der Anhänger des Intuitionismus sprachen, in Wirklichkeit nichts zu spüren war.
Die endgültige Anerkennung der ZF-Mengelehre in der Praxis zog sich allerdings noch über längere Zeit hin. Wesentlich trug dazu die Initiative der Mathematiker-Gruppe mit Pseudonym Nicolas Bourbaki bei; sie wollte die Mathematik auf der Basis Mengenlehre einheitlich neu darstellen und setzte dies ab 1939 in zentralen Mathematikgebieten erfolgreich um. In den 1960er Jahren wurde es dann allgemein bekannt, dass sich die ZF-Mengenlehre als Grundlage der Mathematik eignet. Es gab sogar einen vorübergehenden Zeitraum, in dem die Mengenlehre in der Grundschule behandelt wurde.
Parallel zur Erfolgsgeschichte der Mengenlehre blieb jedoch auch die Diskussion der Mengenaxiome in der Fachwelt aktuell. Es entstanden auch alternative axiomatische Mengenlehren, etwa 1940 die Neumann-Bernays-Gödel-Mengenlehre, die ZF auf Klassen verallgemeinert, oder 1955 die Ackermann-Mengenlehre, die neu an Cantors Mengendefinition anknüpfte.
Definitionen
In der reinen Mengenlehre ist das Elementprädikat
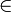 die einzige notwendige Grundrelation. Alle mengentheoretischen Begriffe und Aussagen werden aus ihr mit logischen Operatoren der Prädikatenlogik definiert.
die einzige notwendige Grundrelation. Alle mengentheoretischen Begriffe und Aussagen werden aus ihr mit logischen Operatoren der Prädikatenlogik definiert.Teilmenge
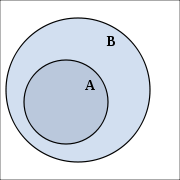
Eine Menge A heißt Teilmenge einer Menge B, wenn jedes Element von A auch Element von B ist.
B wird dann Obermenge (selten: Übermenge) von A genannt. Formal:
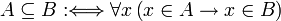 .
.
A ist echte Teilmenge von B (oder B ist echte Obermenge von A), wenn A Teilmenge von B ist, aber von B verschieden, also jedes Element aus A auch Element von B ist, aber (mindestens) ein Element in B existiert, das nicht in A enthalten ist.
Die Relation „ist Teilmenge von“ bildet eine Halbordnung. Die Relation „echte Teilmenge“ ist eine strenge Halbordnung.
Es gibt zwei Notationen:
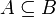 für „Teilmenge“ und
für „Teilmenge“ und 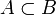 für „echte Teilmenge“ oder
für „echte Teilmenge“ oder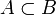 für „Teilmenge“ und
für „Teilmenge“ und 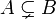 für „echte Teilmenge“.
für „echte Teilmenge“.
In diesem Artikel wird das erstgenannte System verwendet, es sind jedoch beide weit verbreitet.
Die Negation der Relationen
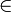 ,
, 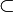 und
und 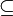 kann durch das durchgestrichene jeweilige Relationssymbol bezeichnet werden, also zum Beispiel durch
kann durch das durchgestrichene jeweilige Relationssymbol bezeichnet werden, also zum Beispiel durch 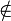 . Außerdem ist es möglich, die Reihenfolge der beiden Argumente zu vertauschen, wenn dabei auch das Relationssymbol umgedreht wird. So kann also anstelle von
. Außerdem ist es möglich, die Reihenfolge der beiden Argumente zu vertauschen, wenn dabei auch das Relationssymbol umgedreht wird. So kann also anstelle von 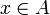 auch
auch 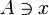 , anstelle von
, anstelle von 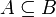 auch
auch 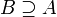 und anstelle von
und anstelle von 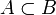 auch
auch 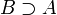 geschrieben werden. Auch ein gleichzeitiges Durchstreichen und Umdrehen dieser Relationssymbole ist denkbar.
geschrieben werden. Auch ein gleichzeitiges Durchstreichen und Umdrehen dieser Relationssymbole ist denkbar.Gleichheit
Zwei Mengen heißen gleich, wenn sie dieselben Elemente enthalten.
Diese Definition bezeichnet die Extensionalität und damit die grundlegende Eigenschaft von Mengen. Formal:
Tatsächlich muss eine Menge A aber meist intensional beschrieben werden. Das heißt: Es wird eine Aussageform P(x) angegeben (mit einer Objektvariablen x, die eine wohlbestimmte Definitionsmenge D haben sollte), sodass
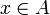 genau dann gilt, wenn P(x) zutrifft. Dafür schreibt man dann:
genau dann gilt, wenn P(x) zutrifft. Dafür schreibt man dann:Zu jeder Menge A gibt es viele verschiedene Aussageformen P(x), die diese beschreiben. Die Frage, ob zwei gegebene Aussageformen P(x) und Q(x) dieselbe Menge beschreiben, ist keineswegs trivial. Im Gegenteil: Viele Fragestellungen der Mathematik lassen sich in dieser Form formulieren: „Sind
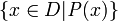 und
und  die gleiche Menge?“
die gleiche Menge?“Viele Gleichheitsbeweise benutzen die Äquivalenz
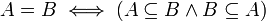 .
.Leere Menge
Die Menge, die kein Element enthält, heißt leere Menge. Sie wird mit
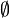 oder auch {} bezeichnet. Aus der Extensionalität der Mengen folgt, dass es nur eine leere Menge gibt: Jede „andere“ leere Menge enthält dieselben Elemente (nämlich keine), ist also gleich. Folglich sind
oder auch {} bezeichnet. Aus der Extensionalität der Mengen folgt, dass es nur eine leere Menge gibt: Jede „andere“ leere Menge enthält dieselben Elemente (nämlich keine), ist also gleich. Folglich sind 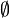 und
und 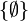 verschieden, da letztere Menge eine andere Menge als Element enthält. Die leere Menge ist Teilmenge einer jeden Menge.
verschieden, da letztere Menge eine andere Menge als Element enthält. Die leere Menge ist Teilmenge einer jeden Menge.Schnittmenge
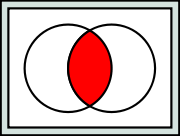
Gegeben ist eine nichtleere Menge U von Mengen. Die Schnittmenge (auch Durchschnittsmenge) von U ist die Menge der Elemente, die in jedem Element von U enthalten sind. Formal:
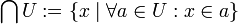 .
.
Ist U eine Paarmenge, also
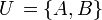 , so schreibt man für
, so schreibt man für 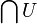 gewöhnlich
gewöhnlichund liest dies: A geschnitten mit B (oder: Der Durchschnitt von A und B) ist die Menge aller Elemente, die sowohl in A als auch in B enthalten sind.
Diese Schreibweise lässt sich leicht auf den Durchschnitt aus endlich vielen Mengen
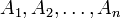 verallgemeinern.
verallgemeinern.Eine ältere Bezeichnung hierfür ist inneres Produkt oder Produkt erster Art. Dieses wird dann auch geschrieben
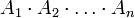 oder
oder 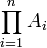
Abweichende Schreibweise für den Durchschnitt aus beliebig vielen Mengen:
Die Elemente der Menge U, die ja selbst wieder Mengen sind, werden mit Aλ bezeichnet. Es wird eine „Indexmenge“ Λ(Lambda) eingeführt, sodass
 ist. Die Schnittmenge
ist. Die Schnittmenge 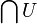 wird dann geschrieben als:
wird dann geschrieben als: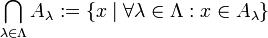 ,
,
also die Menge aller Elemente, die in sämtlichen Mengen Aλ enthalten sind.
Vereinigungsmenge
Dies ist der zu Schnittmenge duale Begriff: Die Vereinigungsmenge von U ist die Menge der Elemente, die in mindestens einem Element von U enthalten sind. Formal:
 .
.
Im Gegensatz zu
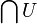 ist
ist 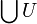 auch dann erklärt, wenn U leer ist, und zwar ergibt sich
auch dann erklärt, wenn U leer ist, und zwar ergibt sich 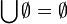 .
.Für
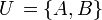 schreibt man wieder
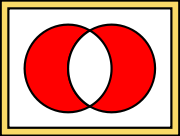
schreibt man wiederund liest dies: A vereinigt mit B (oder: Die Vereinigung von A und B) ist die Menge aller Elemente, die in A oder in B enthalten sind. Das „oder“ ist hier nicht-ausschließend zu verstehen. Die Vereinigung umfasst auch die Elemente, die in beiden Mengen enthalten sind.
Auch diese Schreibweise ist für die Vereinigung endlich vieler Mengen geeignet.
Als ältere Bezeichnung hierfür wird zuweilen noch Summe verwendet und dann geschrieben
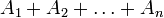 oder
oder 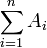 .
.
Vorsicht: Der Begriff Summe wird heute auch für die disjunkte Vereinigung von Mengen benutzt.
Unter Verwendung der Indexmenge Λ schreibt man:
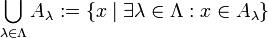 .
.
Differenz und Komplement
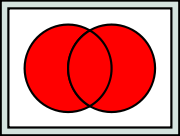
Die Differenz wird gewöhnlich nur für zwei Mengen definiert: Die Differenzmenge (auch Restmenge) von A und B ist die Menge der Elemente, die in A, aber nicht in B enthalten sind. Formal:
Ist
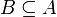 , so heißt die Differenz
, so heißt die Differenz 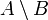 auch Komplement von B in A. Dieser Begriff wird vor allem dann verwendet, wenn A eine Grundmenge ist, die alle in einer bestimmten Untersuchung in Frage stehenden Mengen umfasst. Diese Menge muss dann im Folgenden nicht mehr erwähnt werden, und
auch Komplement von B in A. Dieser Begriff wird vor allem dann verwendet, wenn A eine Grundmenge ist, die alle in einer bestimmten Untersuchung in Frage stehenden Mengen umfasst. Diese Menge muss dann im Folgenden nicht mehr erwähnt werden, undheißt einfach das Komplement von B. Andere Schreibweisen für
 sind
sind 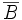 ,
, 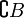 oder B'.
oder B'.Die Menge
wird gelegentlich als symmetrische Differenz von A und B bezeichnet. Es handelt sich um die Menge aller Elemente, die jeweils in einer, aber nicht in beiden der beiden Mengen liegen. Bei Verwendung des ausschließenden Oders (XOR oder
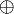 ) kann man dafür auch
) kann man dafür auchschreiben.
Kartesisches Produkt
Die Produktmenge oder das kartesische Produkt, in älterer Terminologie auch Verbindungsmenge oder Produkt zweiter Art, soll hier ebenfalls zunächst als Verknüpfung von zwei Mengen definiert werden:
Die Produktmenge von A und B ist die Menge aller geordneten Paare, deren erstes Element aus A und deren zweites Element aus B ist.
Die Elemente des kartesischen Produkts sind also keine Elemente der Ausgangsmengen, sondern komplexere Objekte, nämlich geordnete Paare. Formal:
Unter der Verwendung von n-Tupeln lässt sich der Begriff leicht für die Verknüpfung endlich vieler Mengen verallgemeinern:
Die Produktbildung ist weder kommutativ noch assoziativ. So sind
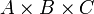 ,
, 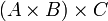 und
und 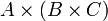 drei verschiedene Mengen, nämlich
drei verschiedene Mengen, nämlich 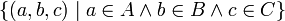 ,
, 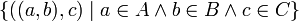 sowie
sowie 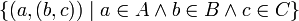 . Aufgrund Bijektionen wie
. Aufgrund Bijektionen wie 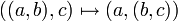 und der daraus folgenden Isomorphie werden diese Mengen oft nicht unterschieden. Die Assoziativität bis auf Isomorphie erlaubt es, beliebige Produktmengen aus einer endlichen Anzahl n von Mengen
und der daraus folgenden Isomorphie werden diese Mengen oft nicht unterschieden. Die Assoziativität bis auf Isomorphie erlaubt es, beliebige Produktmengen aus einer endlichen Anzahl n von Mengen 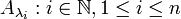 mit der Menge der n-Tupel zu identifizieren und ohne Rücksicht auf die konkrete Klammerung mit
mit der Menge der n-Tupel zu identifizieren und ohne Rücksicht auf die konkrete Klammerung mit  zu bezeichnen.
zu bezeichnen.Für die Produktmenge beliebig vieler Mengen, die durch die Indexmenge Λ benannt werden, schreibt man
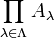 oder, wenn diese Notation schon für „Produkte erster Art“ verwendet wird,
oder, wenn diese Notation schon für „Produkte erster Art“ verwendet wird, 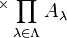 . Für die Definition einer solchen Produktmenge wird ein allgemeiner Funktionsbegriff benötigt. Sie ist die Menge aller Funktionen, die jedem Indexelement λ ein Element der Menge Aλ zuordnen. Formal:
. Für die Definition einer solchen Produktmenge wird ein allgemeiner Funktionsbegriff benötigt. Sie ist die Menge aller Funktionen, die jedem Indexelement λ ein Element der Menge Aλ zuordnen. Formal:Für das Mengenprodukt aus identischen Faktoren gibt es abkürzende Schreibweisen:
- Anstelle des n-fachen endlichen Mengenprodukts
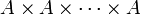 schreibt man auch An.
schreibt man auch An. - Das unendliche Mengenprodukt
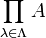 ist kanonisch isomorph zur Menge aller Abbildungen
ist kanonisch isomorph zur Menge aller Abbildungen 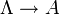 . In Analogie zum endlichen Fall wird dafür die Schreibweise AΛ benutzt.
. In Analogie zum endlichen Fall wird dafür die Schreibweise AΛ benutzt.
Die Mengen
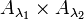 und
und 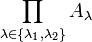 sind nicht notwendig gleich, aber wegen der Bijektion
sind nicht notwendig gleich, aber wegen der Bijektion  mit
mit  ,
, 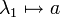 ,
, 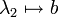 zueinander isomorph. Die Definition der zweistelligen Produktmenge ist also mit der Definition der Produktmenge beliebig vieler Mengen konsistent, weshalb für eine endliche nichtleere Produktmenge
zueinander isomorph. Die Definition der zweistelligen Produktmenge ist also mit der Definition der Produktmenge beliebig vieler Mengen konsistent, weshalb für eine endliche nichtleere Produktmenge 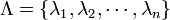 in der Regel auch nicht zwischen
in der Regel auch nicht zwischen 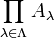 und
und  unterschieden wird.
unterschieden wird.Potenzmenge
Die Potenzmenge
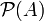 von A ist die Menge aller Teilmengen von A.
von A ist die Menge aller Teilmengen von A.Die Potenzmenge von A enthält immer die leere Menge und die Menge A. Somit ist
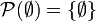 , also eine einelementige Menge. Die Potenzmenge einer einelementigen Menge {a} ist
, also eine einelementige Menge. Die Potenzmenge einer einelementigen Menge {a} ist 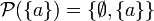 , enthält also zwei Elemente. Allgemein gilt: Besitzt A genau n Elemente, so hat
, enthält also zwei Elemente. Allgemein gilt: Besitzt A genau n Elemente, so hat 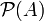 die Elementanzahl 2n. Dies motiviert auch die Schreibweise 2A anstelle
die Elementanzahl 2n. Dies motiviert auch die Schreibweise 2A anstelle 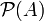 .
.Bei unendlichen Mengen ist der Begriff nicht unproblematisch: Es gibt nachweislich kein Verfahren, das alle Teilmengen auflisten könnte. (Siehe dazu: Cantors zweites Diagonalargument.) Bei einem axiomatischen Aufbau der Mengenlehre (etwa ZFC) muss die Existenz der Potenzmenge durch ein eigenes Potenzmengenaxiom gefordert werden. Diese Fragen hängen eng zusammen mit der Problematik des Auswahlaxioms.
Konstruktive Mathematiker betrachten deshalb die Potenzmenge einer unendlichen Menge als einen grundsätzlich unabgeschlossenen Bereich, zu dem – je nach Fortgang der mathematischen Forschung – immer noch neue Mengen hinzugefügt werden können.
Mächtigkeit und Kardinalzahl
Die Mächtigkeit (Kardinalität) einer Menge A wird mit | A | (zuweilen auch #A) bezeichnet. Bei endlichen Mengen bedeutet | A | die Anzahl der Elemente von A, also eine natürliche Zahl.
Der Menge
 der natürlichen Zahlen lässt sich eine solche Zahl nicht zuordnen. Sie hat offenbar mehr Elemente als jede endliche Zahlenmenge; ihre Kardinalität wird gewöhnlich mit
der natürlichen Zahlen lässt sich eine solche Zahl nicht zuordnen. Sie hat offenbar mehr Elemente als jede endliche Zahlenmenge; ihre Kardinalität wird gewöhnlich mit  bezeichnet.
bezeichnet.Betrachtet man die Menge
 und ihre Potenzmenge als aktual unendliche Mengen, so ergeben sich verschiedene Grade der Unendlichkeit, die als Kardinalzahlen bezeichnet werden. Die Gesamtheit der Kardinalzahlen erweist sich dann als zu groß, um noch als Menge begriffen zu werden.
und ihre Potenzmenge als aktual unendliche Mengen, so ergeben sich verschiedene Grade der Unendlichkeit, die als Kardinalzahlen bezeichnet werden. Die Gesamtheit der Kardinalzahlen erweist sich dann als zu groß, um noch als Menge begriffen zu werden.Gleichwohl ist der Begriff Kardinalzahl eine Verallgemeinerung der Elementanzahl einer (endlichen) Menge. Unter Einbeziehung der Arithmetik der Kardinalzahlen wird die Mächtigkeit der Potenzmenge von A, auch bei unendlichen Mengen, mit 2 | A | bezeichnet.
Die Kardinalzahl der Potenzmenge von
 ,
, 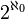 , also die Kardinalzahl der reellen Zahlen, wird mit c oder mit
, also die Kardinalzahl der reellen Zahlen, wird mit c oder mit 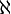 bezeichnet. Die Frage, ob diese Zahl
bezeichnet. Die Frage, ob diese Zahl 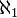 (die nächstgrößere Kardinalzahl nach
(die nächstgrößere Kardinalzahl nach  ) ist, ist Gegenstand der Kontinuumshypothese.
) ist, ist Gegenstand der Kontinuumshypothese.Anmerkungen
- Für eine endliche, nicht leere Indexmenge
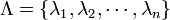 gilt
gilt  und
und 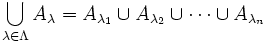 . Die Definitionen für den zweistelligen Fall und den Fall beliebig vieler Mengen sind also zueinander konsistent.
. Die Definitionen für den zweistelligen Fall und den Fall beliebig vieler Mengen sind also zueinander konsistent. - Es gilt
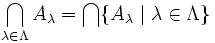 und
und 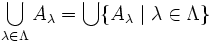 .
. - Für den leeren Schnitt liefert die Definition:
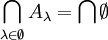 ist eine als vorgegeben vorausgesetzte Menge, die alle Aλ enthält, das kann z. B. der gesamte Raum sein, wenn man gerade einen Raum – in irgend einem math. Sinne – betrachtet (ohne eine solche Voraussetzung ergibt der leere Schnitt keinen Sinn!), für die leere Vereinigung:
ist eine als vorgegeben vorausgesetzte Menge, die alle Aλ enthält, das kann z. B. der gesamte Raum sein, wenn man gerade einen Raum – in irgend einem math. Sinne – betrachtet (ohne eine solche Voraussetzung ergibt der leere Schnitt keinen Sinn!), für die leere Vereinigung: 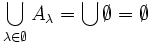 und für die leere Produktmenge gilt:
und für die leere Produktmenge gilt:  ist eine Menge mit genau einem Element, nämlich der „leeren Funktion“ (sie ist in
ist eine Menge mit genau einem Element, nämlich der „leeren Funktion“ (sie ist in 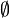 definiert), welche man mit der leeren Menge gleichsetzen kann (wenn man eine Funktion als eine Menge von Paaren – mit einer zusätzlichen Bedingung – definiert, dann ist die leere Funktion tatsächlich gleich der leeren Menge)
definiert), welche man mit der leeren Menge gleichsetzen kann (wenn man eine Funktion als eine Menge von Paaren – mit einer zusätzlichen Bedingung – definiert, dann ist die leere Funktion tatsächlich gleich der leeren Menge)
Beispiele
Wir betrachten die Mengen X = {1,2,3}, A = {1,2} und B = {1,3}. Es gelten:
 ,
, 
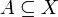 ,
,  ,
, 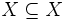
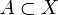 ,
, 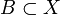

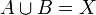
- Für die Komplemente bezüglich X gilt
 ,
,  ,
,  ,
,  .
. 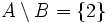 ,
,  ,
, 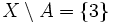 ,
, 
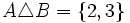 ,
, 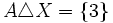 ,
, 
- | X | = 3, | A | = | B | = 2,
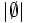 = 0,
= 0, 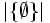 = 1
= 1 

 ,
,  , A2 = {(1,1),(1,2),(2,1),(2,2)}, {3}3 = {(3,3,3)}
, A2 = {(1,1),(1,2),(2,1),(2,2)}, {3}3 = {(3,3,3)}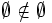 ,
, 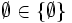
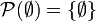 ,
, 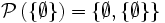
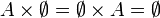
Gesetzmäßigkeiten
Die Menge
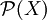 ist bezüglich der Relation
ist bezüglich der Relation 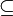 partiell geordnet, denn für alle
partiell geordnet, denn für alle 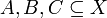 gilt:
gilt:- Reflexivität:
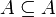
- Antisymmetrie: Aus
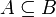 und
und 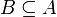 folgt A = B
folgt A = B - Transitivität: Aus
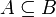 und
und 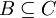 folgt
folgt 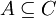
Die Mengen-Operationen Schnitt
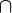 und Vereinigung
und Vereinigung  sind kommutativ, assoziativ und zueinander distributiv:
sind kommutativ, assoziativ und zueinander distributiv:Für die Differenzmenge gelten folgende Gesetzmäßigkeiten:
- Assoziativgesetze:
 und
und 
- Distributivgesetze:
 ,
, 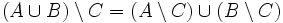 ,
, 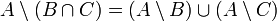 und
und 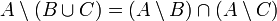
Für die symmetrische Differenz gelten folgende Gesetzmäßigkeiten:
- Assoziativgesetz:

- Kommutativgesetz:
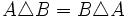
- Distributivgesetz:
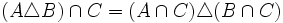
Die Algebra der Mengen ist eine sogenannte Boolesche Algebra.
Andere Konzepte
Als Grundlage der Informatik reicht die typenfreie Mengenlehre nach Zermelo und Fraenkel allein nicht aus, da sie hochgradig unkonstruktiv ist, also den Begriff des Algorithmus kaum erfasst. Aus diesem Grunde wurden seit den 1970er Jahren konstruktive Kalküle entwickelt, die Klassifizierungskonzepte wie Datentypen usw. beinhalten. Es wird behauptet, dass diese Theorien im Hinblick auf Universalität und Anwendungsbereich der klassischen Mengentheorie gleichkommen.
Eine alternative Mengentheorie kann man aufbauend auf der Kategorientheorie mit Hilfe von Topoi definieren.
Siehe auch
Weblinks
- Eintrag in der Stanford Encyclopedia of Philosophy (englisch, inklusive Literaturangaben)
- José Ferreirós (2007): 'The Early Development of Set Theory' Eintrag in der Stanford Encyclopedia of Philosophy (englisch, inklusive Literaturangaben)
- Mathematical Atlas Artikel
- PlanetMath Artikel
- Mathe Online
Einzelnachweise
- ↑ Georg Cantor: Beiträge zur Begründung der transfiniten Mengenlehre. In: Mathematische Annalen46 (1895), S. 31.
- ↑ Richard Dedekind: Stetigkeit und irrationale Zahlen. Braunschweig 1872.
- ↑ Richard Dedekind: Was sind und was sollen die Zahlen? Braunschweig 1888.
- ↑ Giuseppe Peano: Arithmetices Principia nova methodo exposita. Turin 1889.
- ↑ Brief von Cantor an Dedekind vom 31. August 1899, in: Georg Cantor: Gesammelte Abhandlungen mathematischen und philosophischen Inhalts. ed. E. Zermelo, Berlin 1932, S. 448.
Literatur
- Heinz-Dieter Ebbinghaus: Einführung in die Mengenlehre. Spektrum Akademischer Verlag, Heidelberg–Berlin 2003, ISBN 3-8274-1411-3.
- Adolf Fraenkel: Einleitung in die Mengenlehre. Springer Verlag, Berlin–Heidelberg–New York 1928. Neudruck: Dr. Martin Sändig oHG, Walluf 1972, ISBN 3-500-24960-4.
- Paul R. Halmos: Naive Mengenlehre. Vandenhoeck & Ruprecht, Göttingen 1968, ISBN 3-525-40527-8.
- Felix Hausdorff: Grundzüge der Mengenlehre. Chelsea Publ. Co., New York 1914, 1949, 1965, ISBN 978-3-540-42224-2
- Erich Kamke: Mengenlehre. 6. Auflage. Walter de Gruyter & Co., Berlin 1969.
- Arnold Oberschelp: Allgemeine Mengenlehre. Mannheim, Leipzig, Wien, Zürich, 1994.
- André Joyal, Ieke Moerdijk: Algebraic Set Theory. Cambridge University Press, 1995, ISBN 0521558301.
Wikimedia Foundation.

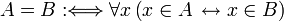

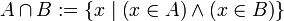


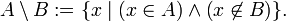
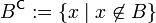
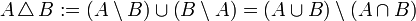
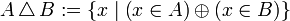
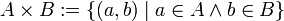
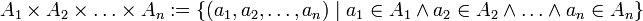
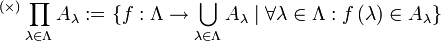
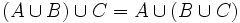 ,
, 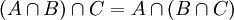
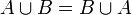 ,
, 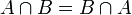
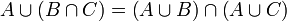
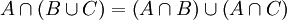
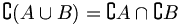 ,
,