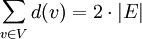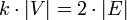Handshake-Lemma

In der Graphentheorie besagt das Handschlaglemma, dass in jedem Graph die Summe der Grade aller Knoten genau doppelt so groß ist wie die Anzahl seiner Kanten.

Formal heißt das: Ist G = (V,E) ein Graph (bei gerichteten Graphen werden sowohl die Ein- als auch die Ausgangs-Grade gezählt), so gilt also mit dem Grad d(v) eines Knotens v aus V:

$\sum_{v\in V} d(v) = 2\cdot |E|$

Daraus folgt sofort, dass jeder Graph eine gerade Anzahl von Knoten ungeraden Grades hat.

Bei regulären Graphen vereinfacht sich die Formel. Für einen k-regulären Graphen gilt:

$k\cdot |V| = 2\cdot |E|$

Literatur

• Lutz Volkmann: Graphen und Digraphen, Springer (Wien) 1991, ISBN 3-211-82267-4, S.6

Weblinks

• Handschlag-Lemma auf PlanetMath (engl.)