Hazardfunktion

Der Hazardwert (auch Hazardrate; engl. hazard: Zufall, Risiko) ist ein Element der Verweildaueranalyse in der Statistik. Er gibt grob gesprochen die Wahrscheinlichkeit dafür an, dass zu einem festen Zeitpunkt ein bestimmtes "Austrittsereignis" (beispielsweise Tod einer Person, Verkauf einer Ware, Zerfall eines radioaktiven Elements) eintritt. Man spricht auch von einer momentanten Neigung zum Zustandswechsel.

Definition

Es sei 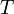$T\;$ eine nicht-negative Zufallsvariable mit Verteilungsfunktion 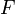$F\;$, die den Zeitpunkt des Zustandswechsels eines Objektes angibt. Dann ist die zugehörige Hazardfunktion zum Zeitpunkt 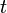$t\;$ definiert als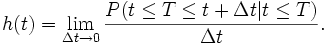

$h(t) = \lim_{\Delta t \to 0} \frac{P(t \leq T \leq t + \Delta t|t \leq T)}{\Delta t}.$

Der Zähler des obigen Ausdrucks bezeichnet dabei eine bedingte Wahrscheinlichkeit. Die Hazardfunktion entspricht also der Rate, mit der ein Zustandswechsel zum Zeitpunkt 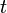$t\;$ stattfindet, wenn bekannt ist, dass dieser Wechsel bis dahin nicht stattgefunden hat.

Es ist leicht zu zeigen, dass die folgende Identität gilt:

$h(t) = \frac{f(t)}{1-F(t)},$

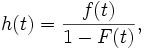
wobei 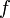$f\;$ die Dichtefunktion von T bezeichnet. Daher ist die Hazardfunktion im allgemeinen auch selbst keine Dichtefunktion. Hazardfunktionen werden oft in der Ereigniszeitanalyse gebraucht, der Zusammenhang zur Überlebenszeitfunktion 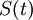$S(t)\;$ ist durch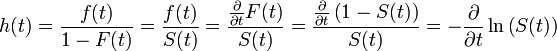

$h(t) = \frac{f(t)}{1-F(t)} = \frac{f(t)}{S(t)} = \frac{\frac{\partial}{\partial t}F(t)}{S(t)} = \frac{\frac{\partial}{\partial t}\left( 1 - S(t) \right)}{S(t)} = - \frac{\partial}{\partial t} \ln\left(S(t)\right)$

gegeben.

Beispiel

Verkauf von Harddisks aus einem Lager:

                      Monat     0      1     2      3      4      5
                    Verkauf          200   200    400    100    100  
      Bestand am Monatsende  1000    800   600    200    100      0
 Verkaufswahrscheinlichkeit          0.2   0.2    0.4    0.1    0.1
                Hazardwerte          0.2   0.25   0.66   0.5      1

Berechnung

0.2/[1000/1000] = 0.2
0.2/[800/1000]  = 0.25
0.4/[600/1000]  = 0.66
0.1/[200/1000]  = 0.5
0.1/[100/1000]  = 1

Siehe auch

Mean Time Between Failures

Weblinks

• ILMES (Internet-Lexikon der Methoden der empirischen Sozialforschung): Verweildaueranalyse